Технологическая карта урока «Подобные треугольники»
Описание урока
|
Предмет
|
Геометрия
|
Класс
|
8
|
Тема урока
|
Подобные треугольники
|
Тип урока
|
Урок «открытия» нового знания
|
Цель урока
|
Познакомить с новым понятием «подобные треугольники»; формировать умения использовать полученные знания при решении задач.
|
Планируемые резльтаты
|
Предметные: обучающиеся получать представление о подобных треугольника, сходственных сторонах и коэффициенте подобия; научаться применять полученные знания при решении практических задач.
Метапредметные: анализировать и осмысливать изучаемый теоретический материал; самостоятельно определять цель учебной деятельности; планировать свою деятельность и прогнозировать ее результат; строить речевые высказывания в устной форме; сравнивать и выделять главное; строить логические цепочки рассуждений; действовать в соответствии с алгоритмом; работать с текстом учебника, таблицами, сетью Интернет.
Личностные: понимать смысл поставленной задачи; осуществлять саоконтроль и взаимоконтроль, осознавать связь обучения с повседневной жизнью, развивать чувство товарищества, взаимопомощи, умение слышать других, учвствовать в диалоге.
|
Межпредметные связи
|
Реализация межпредметных связей с алгеброй, географией, литературой, историей
|
Методы обучения
|
Частично-поисковый, исследовательская деятельность, объяснительно-иллюстративный, словестный (беседа, диалог), наглядный (работа с рисунками, схемами и моделями), практический.
|
Формы организации познавательной деятельности обучающихся
|
Фронтальная, индивидуальная, в парах.
|
Этапы урока
|
Деятельность учителя
|
Деятельность обучающихся
|
Формируемые УУД
|
1.Этап мотивации к учебной деятельности
|
Я приглашаю вас сегодня пополнить наши знания о геометрических фигурах.
Представьте себе, что Вы прибыли с важным визитом в страну Восходящего Солнца. В какую страну мы прибыли?
Нам необходимо расположить наших партнеров с японской стороны к нашему проекту. Как известно дружба начинается с улыбки, а деловые отношения с приветствия. Как нужно поприветствовать, чтобы переговоры прошли успешно?
Поприветствуйте друг друга по-японски
Я предлагаю вам стать друг против друга и поклониться, причем, чем ниже поклон, тем больше уважения вы проявите друг к другу, проявим наше уважение и присутствующим здесь гостям.
|
Организуют рабочее место. Участвуют в беседе, приветствии, вспоминают Страну Восходящего солнца-Японию, как там осуществляется приветствие.
|
Умение соблюдать дисциплину на уроке, уважительно относится к учителю, одноклассникам.
|
2. Этап актуализации и пробного учебного действия.
|
Начнем наш урок со следующего задания
- Распределите данные фигуры по группам.
-По какому принципу вы распределяли фигуры: по цвету, по размеру, по форме?
-Какие фигуры попали в одну группу?
-Какая фигура не попала ни в какую группу? Почему?
-Как одним словом можно назвать фигуры, попавшие в одну группу?
В геометрии фигуры, которые имеют одинаковую форму, называют подобными. Например, два круга подобны.
В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить.
Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида. А еще его называют “дьявольским”, “проклятым”. Загадочность его заключается в том, что в нем бесследно исчезают корабли и самолеты. Природа этого места остается, тайной и по сей день.
Как вы думаете, что это за место?
Так, какой геометрической фигуре посвятим наш урок?
-Сформултруйте тему урока ПОДОБнЫЕ ТРЕУГОЛЬНИКИ.
-Как Вы думаете, что будет являтся целями нашего урока?
(-узнать какие треугольники называются подобными
-как найти, определить что треугольники подобные,
-научиться применять подобие треугольников при решении задач)
-Какие ассоциации у Вас возникают со словами Подобные треугольники?
Сейчас я предлагаю провести геометрическую разминку, посвященную треугольнику. Давайте попробуем вспомнить все, что нам известно о треугольнике. Работа с карточками
Вопросы:
-Какая фигура называется треугольником?
-Какие элементы треугольника вы знаете?
-Какими могут быть треугольники в зависимости от величины углов, длин сторон?
-Расскажите о равнобедренном треугольнике; о равностороннем треугольнике; о прямоугольном треугольнике.
-Чему равна сумма углов треугольника?
-Ребята, в следующем году нам с Вами предстоит экзамен и при подготовке к экзамену мы будем работать с различными обобщающими таблицами. Сегодня я предлагаю Вам элемент таблицы и прошу заполнить пропуски.
-ТАБЛИЦА –заполнить по каким элементам равны треугольники

Оказывается, это еще очень маленькая часть того, что мы должны знать и узнаем в будущем.
ПОВТОРЕНИЕ предыдущей темы
-Ребята, на прошлом уроке мы с Вами повторяли отношения двух чисел.
-Что такое отношение двух чисел? (это их частное)
-Отношение чего мы еще повторяли? (0трезков)
-Что называется отношением отрезков? (Отношение их длин)
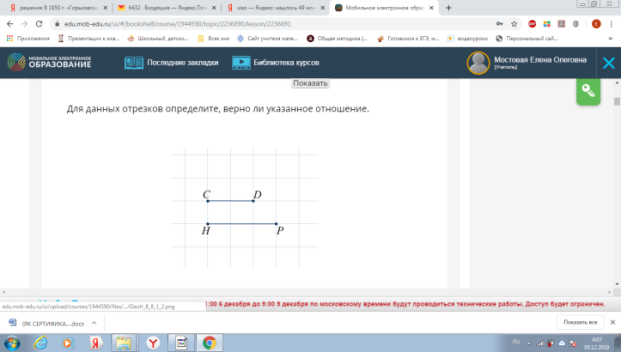
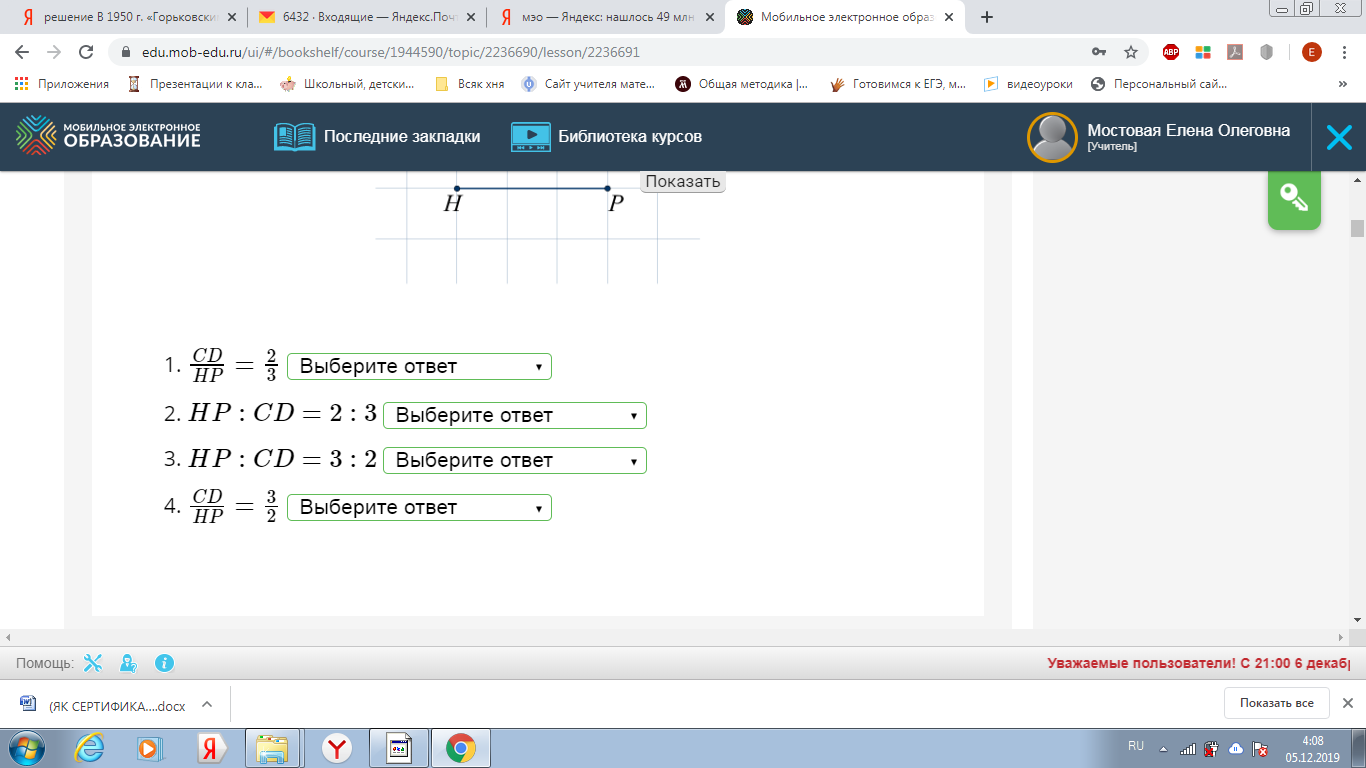
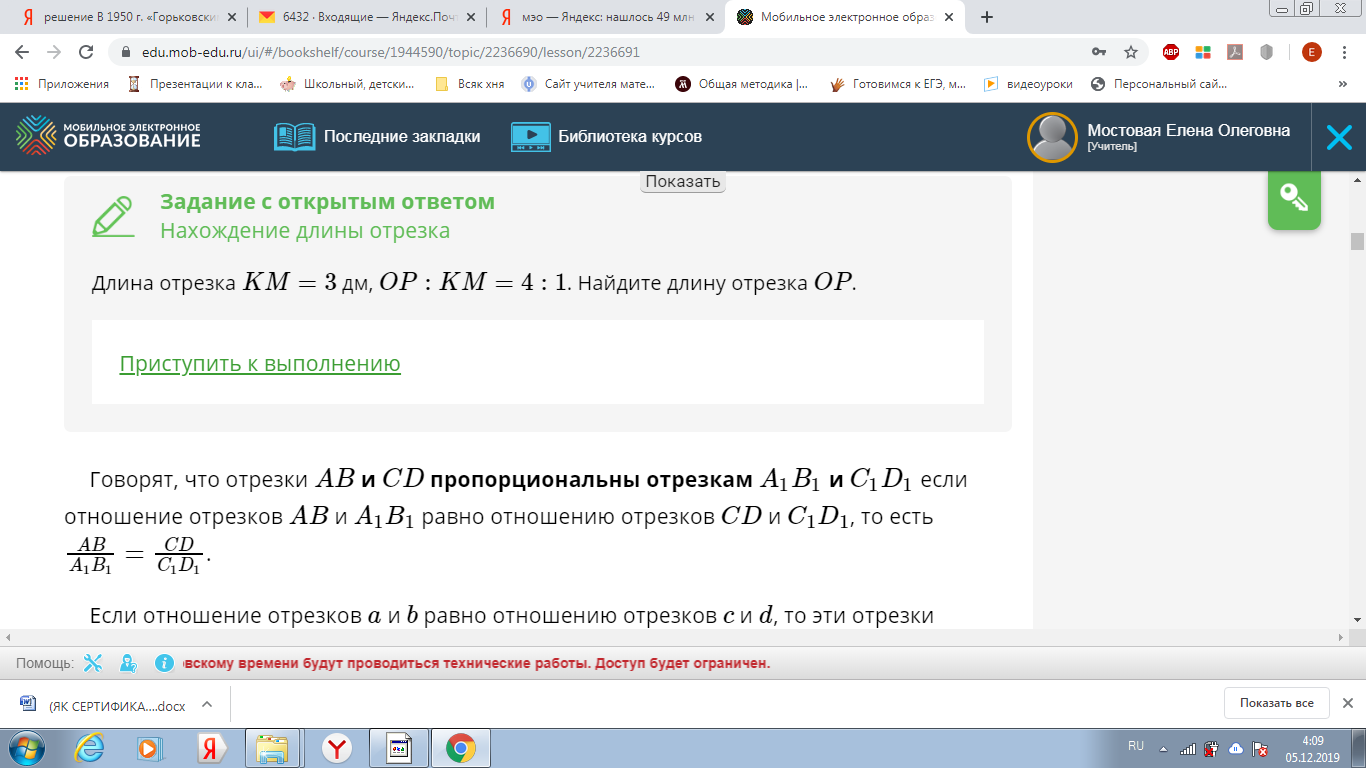
Отрезок АВ=7см, CD=9см, тогда их отношение может выглядеть….
- Что показывает отношение? (во сколько раз первое число больше второго или какую часть первое число составляет от второго).
- Что называют пропорцией? (Равенство двух отношений)
-Сформулируйте основное свойство пропорции.
- Найдите неизвестный член пропорции
х : АВ = MN : KP.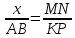
-Ребята, работать мы с Вами сегодня будем в следующих Рабочих листах.
Напишите тему урока, число и ФИО.
Итак первые наши задания на повторение.
Ребята, Вы можете самостоятельно выбрать, сколько заданий Вам решить. Последнее задание сложнее первых.
Масштаб карты 1:18 000 000. Найдите расстояние на карте между столицей Канады и столицей Мексики.
(столица Канады-Оттава, столица Миксики-Мехико, расстояние между ними 3602 км=3602 000 м=3602 000 00 см) Ответ 20 см.
Взаимооценивание по эталону.
Каждое задание оценивается в 2 и 3 балла. Максимум 7 баллов.
-Какие основные понятия мы с Вами повторили? (итог этапа)
|
Выполняют задание учителя, распределяют фигуры по внешнему виду. Знакомятся с понятием подобных финур в геометрии.
Формулируют тему и цели урока.
Работают с кластером «Подобные треугольник».
Активно участвуют в геометрической разминке, работают со справочными материалами.
Повторяют знания по темам: «Отношения», «Пропорции».Затем выполняют задания в рабочих листах по этим темам. Проверка результатов работы по эталону.
|
Умение самостоятельно определять цель учебной деятельности; планировать свою деятельность и прогнозировать ее результат.
|
3. Этап выявления места и причины затруднения.
|
-Я хочу прочитать вам маленькую притчу.
“Усталый пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то сказал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченном троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.
– Кто ты? – спросил верховный жрец?
– Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
– Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? – жрецы согнулись от хохота. – Будет хорошо, – насмешливо продолжал жрец, – если ты ошибешься не более, чем на сто локтей.
– Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.
Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они – жрецы Великого Египта.
– Хорошо, сказал фараон. – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство”.
Кто такой ФАЛЕС? Фале́с — древнегреческий философ и математик из Милета (Малая Азия)
После сегодняшнего урока вы должны предложить свой способ измерения высоты пирамиды, а пока вернемся к нашему треугольник.
|
Слушают легенду о Фалесе, задумываюся о способе измерения высоты пирамиды.
|
Формирование потребности в получении новых знаний.
|
4. Этап построения проекта выхода из затруднения.
|
Показываю два равных треугольника.
- Какие это треугольники?
-Как проверить, что они равны?
Показываю еще 2 треугольника, которые не являются равными
-А что это за треугольники? (Похожие подобные)
-Я предлагаю провести маленькую практическую работу. Идет работа в парах.
Правила работы в парах.
Выслушай партнера, выскажи свое мнение и совместно примите решение.
-Ваша практическая работа будет осуществляться по следующему плану
Измерьте стороны каждого треугольника.
АВ=__ MN=__
ВС=__ NK=__
АС=__ MK=__
Измерьте углы каждого треугольника
∠А=__ ∠M=__
∠В=__ ∠N=__
∠С=__ ∠K=__
Составьте отношения сторон 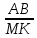 = =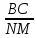 = = 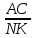 = =
Сделайте вывод: В рассмотренных треугольниках________________________
Затем самопроверка по эталону
-Как вы думаете, как можно назвать эти треугольники? Равноугольные. Похожие.
Эти треугольники подобными треугольниками.
|
Отвечают на вопросы. Работают в парах, исследуют треугольники в соответствии с алгоритмом, с правилами работы в паре.
|
Умение действовать с предложенным алгоритмом.
Осуществление анализа результатов деятельности.
|
5.Этап реализации построенного проекта
|
Пусть у двух треугольников АВС и 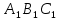 углы соответственно равны ∠А= углы соответственно равны ∠А=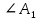 , ∠В= , ∠В=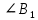 , ∠С= , ∠С=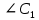 , тогда стороны АВ и , тогда стороны АВ и  АС и АС и 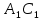 , ВС и , ВС и 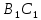 называются сходственными. ЧЕРТЕЖ называются сходственными. ЧЕРТЕЖ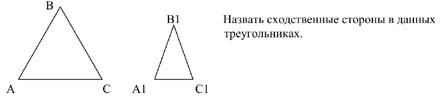
Сходственные стороны – стороны треугольника, лежащие против соответственно равных углов.
Сейчас откройте учебники на стр. 138 и выпишите определение подобных треугольников.
Давайте хором прочитаем.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Обозначение
ΔABC ∼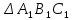 , ,
если равны ∠А=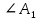 , ∠ В= , ∠ В=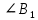 , ∠С= , ∠С=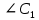 и и
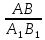 = = 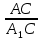 = = 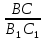 = k = k
k-Коэффициент подобия – число, равное отношению сходственных сторон.
Далее мы изучим, что подобие треугольников можно установить, проверив лишь некоторые из данных равенств.
|
Работают с учителем по новому материалу, самостоятельно с текстом учебника.
|
Анализ и осмысление изучаемого теоретического материала. Работа с текстом учебника.
|
6. Этап первичного закрепления с проговариванием во внешней речи.
|
-А как Вы думаете, подобие фигур встречается только в геометрии?
-Где в жизни можно встретиться с подобными фигурами? (фотографии, планы, карты, макеы, игрушки, различные модели, к примеру учебники биологии птички-подобны настоящим)
ФИЗМИНУТКА
-Покажите каких размеров наша планета земля, а глобус в кабинете географии
Каких размеров кукла у девочек, а рост человека?
Каких размеров дом сторит малыш в садике, а наши дома какой высоты?
-А вообще ребята, мне очень хочется сделать Вам комплимент: Вы сегодня просто бесподобны!!!
-А как этот комплимент связан с темой нашего урока?
ПРОГОВАРИВАНИЕ
Повернитесь друг к другу. Прочитайте по тетрадям наши новые понятия друг другу.
|
Обсуждают связь геометрии с окружающей жизнью. Закрепляют изученные понятия в парах-проговаривают.
|
Воспитание отношения к геометрии как к части общечеловеческой культуры.
|
7. Этап самостоятельной работы по эталону
|
-Какие цели урока уже достигли? Что осталось?
Теперь нам остается применить полученные знания к решению задач.
Задача 1 Треугольники АВС и КОL подобны, ∠А=∠L, ∠В=∠О. Запишите отношение сходственных сторон.УЧИТЕЛЬ
Задача 2 (условие в рабочих листах) УЧИТЕЛЬ или учениек
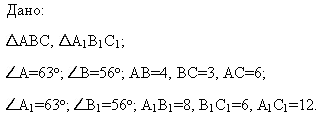
Определить, подобны ли треугольники.
-Скажите, обязательно ли каждый раз прописывать отношение всех трех сходственных сторон, чтобы определить коэффициент k подобия, если известно, что треугольники подобны? Нет, достаточно записать отношение только одной пары сторон.
Задача 3. Определите х.
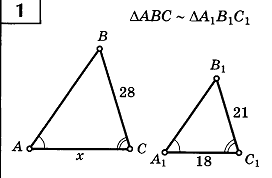
Далее самостоятельное применение полученных знаний
-Запишите отношение сходственных сторон
-Определите МР, если ОР=30 см,АС=17 см, ВС=10 см.
-Выберите неверные утверждения
Любые два равнобедренных треугольника подобны.
Равносторонние треугольники подобны
Две окружности подобны.
Любые два треугольника подобны.
Любые два квадрата подобны.
ВзаимОЦЕНИВАНИЕ ПО ЭТАЛОНУ.
-Чтобы верно выполнить данные задания, что необходимо знать? Как правильно составить отношения сходственных сторон подобных треугольников.
|
Выполняют задания коллективно и самостоятельно, оценивают соседа, сравнивают с эталоном.
|
Формирование умения анализировать текст задачи и намечать план решения. Осуществление самоконтроля.
|
8. Этап рефлексии учебной деятельности на уроке.
|
Подсчитайте количество баллов. Поставьте отметки. Половину из этих отметок выставим в журнал.
-Поднимите руки, у кого 4? 5?
Возврат к целям. Какие цели были поставлены в начале нашего урока?
-Как вы думаете удалось реализовать данные цели?
Вернемся к кластеру, составленному в начале урока. Чем мы его можем еще дополнить?
Возврат к легенде. Фалес «Когда тень от палки будет той же длины, что и сама палка, то длина тени от центра основания пирамиды до ее вершины будет иметь ту же длину, что и сама пирамида». Т. Е. использование подобия треугольников.
-Конечно, на одном уроке успеть познакомиться с новой темой изучить понятия и решить задачу, которую решал еще сам Фалес Милетский-это очень тяжело.Тема «Подобные треугольники»-очень большая и значимая в курсе планеметрии. Нам предстоит решить много подобных задач, также хочется отметить, что во многих вариантах ГИА по математике эта тема также встречается.
-Ребята, приближается Новый год. И сегодня на урок я приготовила вот такую импровизированную елку, которая состоит из чего? подобных треугольников.
-Помогите мне ее украсить.
-На партах у каждого из Вас приготовлены разные опять же треугольники, каждый из них выражает Ваше настроение на уроке. Выберите один (желтый-оранжевый-веселое, синий-равнодушное, спокойное, зеленый-грустное).
А расположить Ваши смайлики на елочке я предлагаю следующим образом.
Верхий ряд-ВСЕ ПОЛУЧИЛОСЬ, ВСЕ ПОНЯЛ
Середина – ВОЗНИКАЛИ ЗАТРУДНЕНИЯ
Нижний ряд-ОСТАЛОСЬ МНОГО ВОПРОСОВ, НУЖНО ХОРОШО ПОРАБОТАТЬ дома
Инструкция к ДЗ.
|
Анализируют результаты своей работы на уроке.
|
Уметь выразить эмоциональное отношение к своим результатам работы на уроке.Качественный анализ результатов своей работы.
| |
 Скачать 0.56 Mb.
Скачать 0.56 Mb.