Описать методику изучения теоремы с учащимися
 Скачать 32.3 Kb. Скачать 32.3 Kb.
|
Описать методику изучения теоремы с учащимися
Описать методику изучения теоремы с учащимися Для этого изучить содержание лабораторной работы №2 (стр.47-59) в учебном пособии «Лабораторные и практические работы по методике преподавания математики» под редакцией Лященко Е.И., выбрать из предложенного списка теорему и описать подробно все этапы работы над теоремой. Поиск доказательства осуществить аналитическим методом. 1.Признак равнобедренного треугольника. 2.Свойство равнобедренного треугольника. 3.Признак параллелограмма. 4.Свойство диагоналей параллелограмма. 5.Свойство противолежащих сторон и углов параллелограмма. 6.Свойство диагоналей ромба. 7.Теорема о средней линии треугольника. 8.Теорема о средней линии трапеции. 9.Теорема Пифагора. 10.Теорема косинусов. 11.Теорема о величине угла, вписанного в окружность. 12.Теорема Фалеса. 13.Теорема синусов. 14. Теорема о внешнем угле треугольника. 15. Теорема Виета. 16. Свойство углов при параллельных прямых и секущей. 17.Признак параллельности прямых (по углам). Задание 1.1 Форма контроля: письменный отчет (документ Word), содержащий ответы на поставленные вопросы. 1. Проанализируйте примерные программы ООО и ОСО и перечислите основные цели обучения математике, раскройте их сущность. 2. Из каких основных разделов состоит программа по математике? 3. Выясните сущность понятия «содержательно-методическая линия школьной программы» (Плакатина О.И. Логико - дидактический анализ состава содержания математического образования). Перечислите содержательно-методические линии современного школьного курса математики. 4. Как в программе для 10-11 классов учитываются потребности профильного обучения? Задание 1.2Литература: Малова И. Е., Горохова С.К. и др. Методика и теория обучения математике в средней школе. См. стр. 231-233 Задание: 1. Изучить методические требования к конспекту урока по математике 2. Изучить технологию составления конспекта урока. 3. Выясните, отвечают ли приведенные для примера технологические карты урока методическим требованиям, о которых упоминается в п.1. Дайте письменный ответ. Техкарта 1 Техкарта 2 Техкарта 3 2. Методика изучения числовых систем в школьном курсе математики Задание по теме «Методические особенности изучения числовой линии в ШКМ» Форма контроля: технологическая карта урока I. Изучить материалы учебного пособия В.П. Покровского «Методика обучения математике: числовая содержательно- методическая линия», знать ответы на вопросы, поставленные автором. II. Разработать технологическую карту указанного фрагмента урока (по вариантам - 4 ВАРИАНТ), сдать в виде электронного документа. 1.Разработать фрагмент урока изучения нового материала по теме «Положительные и отрицательные числа» (6 класс), который демонстрирует методику введения нового понятия. 2. Разработать фрагмент урока изучения нового материала по теме «Понятие об иррациональном числе» (8 класс), который демонстрирует методику введения нового понятия. 3. Разработать фрагмент урока изучения нового материала по теме «Действия с положительными и отрицательными числами» (6 класс), который демонстрирует методику введения и освоения нового правила. 4. Разработать фрагмент урока изучения нового материала по теме «Действия с десятичными дробями» (5 класс), который демонстрирует методику введения и освоения нового правила. 5. Разработать фрагмент урока изучения нового материала по теме «Сложение дробей с разными знаменателями» (6 класс), который демонстрирует методику введения и освоения нового правила. 3. Методика изучения тождественных преобразований Задания по теме «Методика изучения тождественных преобразований» Форма контроля: письменный отчет по заданиям, выполненных индивидуально и презентация, выполненная в Google группой. 1. Изучить содержание раздела «Лекция1. Тождественные преобразования выражений» из методического пособия «Методика изучения математики в основной школе». 2. Выполнить задания №№ 4, 5, 6, 7, стр.18 Указание: № 7 выполнить по вариантам: в каждом варианте одно из понятий. 4. Методика изучения уравнений и неравенств Задания по теме «Методика изучения уравнений и неравенств» Форма контроля: письменный отчет (документ Word) 1. Изучить содержание раздела «Лекция 2. Содержательная линия «Уравнения и неравенства» в школьном курсе математики» из методического пособия «Методика изучения математики в основной школе». 2. Выполнить следующие задания, предлагаемые авторами пособия: Задание 1(стр.27-28) (пункты 1-3); Задание 2(стр. 29) (пункты 2,3) Задание 3 (стр.30) (пункт 1+презентация) Задание 4 (стр.31) (пункты 2,3) Задание 5 (стр.34) (пункты 1,2) Задание 6 (стр.37) (пункты 1,2) Задание 7 (стр. 40) (пункты 1,2) Пояснение. Схемы логико - математического и логико-дидактического анализа основных компонентов содержания материала можно найти в учебном пособии «Лабораторные и практические работы по методике преподавания математики» под редакцией Лященко Е.И. 5. Методика изучения функций в школьном курсе математики Задания по теме «Методика изучения функций в школьном курсе математики» Форма контроля: технологические карты 2 уроков, письменная контрольная работа (документ Word) 1.Изучите содержание пункта 1.1 учебного пособия В.П. Покровского «Методика обучения математике: функциональная содержательно- методическая линия». Выполните следующие задания: Сформулируйте основные этапы исторического развития понятия функции в математике и характерные их черты, приведите различные определения функции (И. Бернулли, Л. Эйлера, Н. И. Лобачевского, П. Дирихле) и раскройте их особенности, используя краткие исторические экскурсы из школьных учебников. Установите с помощью общеобразовательного стандарта (примерных программ) обязательное содержание учебного материала функциональной линии по 7 – 9-м и 10 – 11-м классам (базовый и профильный уровни). Составьте схему понятийного аппарата Какие виды числовых функций изучаются в основной и старшей школах? На основе изучения примерной программы по математике выделите цели изучения функционального материала и соответствующие требования к математической подготовке учащихся. Удалось ли реализовать в современных школьных учебниках по математике идеи Ф. Клейна о том, что функция должна играть основную, руководящую роль в курсе средней школы; функция должна появиться очень рано и должна пронизать все преподавание алгебры и геометрии; понятие функции в геометрической форме должно быть вообще душой школьного математического образования. Ответ по каждой позиции обосновать. 2. Изучите содержание пункта 1.2 учебного пособия В.П. Покровского «Методика обучения математике: функциональная содержательно- методическая линия» и выполните задания: Выпишите определения функции из действующих школьных учебников алгебры 7 – 9-х классов и сравните их (2-3 учебника). Обратите внимание на место введения явного определения. Выпишите определения функции из действующих школьных учебников алгебры и начал анализа для 10 – 11-х классов и сравните их, выясните преемственность с определениями основной школы. Какое на ваш взгляд определение функции можно считать дидактически целесообразным для учащихся 7 – 9-х (10 – 11-х) классов? Ответ обоснуйте. 3. Изучите содержание пункта 1.3 учебного пособия В.П. Покровского «Методика обучения математике: функциональная содержательно- методическая линия» и выполните задание: Подберите упражнения, которые целенаправленно готовят учащихся к введению понятия функции, способов ее задания, области определения функции. 4. Изучите содержание пункта 1.4 учебного пособия В.П. Покровского «Методика обучения математике: функциональная содержательно- методическая линия» и выполните задания: Известно, что у учащихся вызывают интерес примеры, когда функциональной зависимости нет. Например, мы говорим, что масса человека зависит от его роста, но нельзя сказать, что масса человека есть функция его роста. Приведите еще несколько примеров. Есть ли они в учебниках? Решая задачу: «Построить график функции, заданной формулой y= 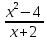 , ученик построил график функции, заданной формулой y = x – 2. Какие ошибки он допустил? Как убедить его в ошибочности решения. Являются ли ошибки грубыми или их можно отнести к недочетам? , ученик построил график функции, заданной формулой y = x – 2. Какие ошибки он допустил? Как убедить его в ошибочности решения. Являются ли ошибки грубыми или их можно отнести к недочетам? Составьте техкарту урока по введению понятия функции на основе одного из учебников по алгебре. Как показать ученикам, что не всякая формула задает функцию и не всякую функцию можно задать формулой. Приведите примеры нечисловых функций и укажите для них области определения и значений. 5. Изучите пункт 1.5 и выполните задание: Составьте для каждого комплекта учебников таблицу рассмотрения свойств функций с указанием времени изучения (класс) и уровня строгости (использовать обозначения для уровней: Н – наглядно-интуитивный, О – словесно-описательный, Ф-формальный). Например, по учебникам А. Г. Мордковича начало таблицы может выглядеть так:
Сравните составленные таблицы по времени изучения свойств и их уровню строгости. Какой из авторских подходов вы считаете наиболее удачным? Проследите динамику развития двух-трех свойств функции. 6. Изучите пункт 2.1. и выполните задания: Составьте сравнительный анализ учебников алгебры по перечисленным в тексте пункта разночтениям. Известно, что линейная функция задается указанием чисел k и b. Оформите таблицу графиков функции в зависимости от сочетания числовых значений k и b (k>0 при b>0, b =0, b<0; k<0 при b<0, b=0, b>0; k=0 при b>0, b =0, b<0) Составьте техкарту урока по введению понятия линейной функции 7. Изучите пункт 2.2 и выполните задания: Составьте таблицу графиков квадратичной функции в зависимости от значений коэффициента а и дискриминанта D (а ˃ 0, а ˂ 0, D ˃ 0, D ˂ 0, D=0), а также таблицы ее вариантов для b ≠ 0, c˃ 0 и c ˂ 0; b˃0 и b˂0 и с=0; b=c=0; b=0 при а ˃0 и с 0, а˂0 и с˂0, а˃0 и с=0, а˂0 и с=0, а˃0 и с˂0, а˂0 и с˂0. Опишите методику их использования. Составьте методическую схему изучения квадратичной функции и ее частных случаев по различным учебникам. Сформулируйте результаты изучения квадратичной функции в основной и старшей школе. 8. Изучите пункт 2.3 и выполните задания: Составьте перечень свойств функций 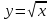 и и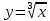 . Обратите внимание на учебник А.Г. Мордковича, где они наиболее полно представлены на уровне основной школы. . Обратите внимание на учебник А.Г. Мордковича, где они наиболее полно представлены на уровне основной школы. Изучите материал учебника М.И. Башмакова о взаимно обратных функциях. Выскажите своё мнение о доступности его для учащихся 9-го класса. 6. Методика изучения геометрии в школьном курсе математики Задание 6 Задания по теме «Методика изучения геометрии в школьном курсе математики» Форма контроля: письменный отчет по заданиям 2,3, 5, 6,7(документ Word) 1. Изучить в учебном пособии Н.М. Рогановского, Е.Н. Рогановской «Методика преподавания математики в средней школе. Часть 2» Тему 5, стр. 124-158. 2. Охарактеризуйте основные содержательные линии геометрии и их наполнение по различным годам обучения. Выполните обзор действующих учебников с этой точки зрения. 3. Разработайте структурированный рисунок к доказательству второго признака равенства треугольников. 4. Изучить в учебном пособии Н.М. Рогановского, Е.Н. Рогановской «Методика преподавания математики в средней школе» Тему 6, стр. 159-195. 5. Разработайте фрагмент урока по решению прямоугольного треугольника. Фрагмент должен содержать разработанную студентом систему указаний и вопросов, с помощью которых можно направлять процесс поиска решения задач. 6. Изучить в учебном пособии Н.М. Рогановского, Е.Н. Рогановской «Методика преподавания математики в средней школе» Тему 7, стр. 196-226. Выполните задание 5 на стр. 227. 7. Изучить в учебном пособии Н.М. Рогановского, Е.Н. Рогановской «Методика преподавания математики в средней школе» Тему 8, стр. 229-257 и выполнить задания 3, 4 на стр. 257. Для выполнения заданий используйте учебники: 1. Атанасян Л. С, Бутузов В.Ф., Кадомцев СБ. и др. Геометрия. 7-9 классы 2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Геометрия, 7 3. Мерзляк А.Г., Полонский В.Б., Якир М.С. Геометрия, 8 4. Мерзляк А.Г., Полонский В.Б., Якир М.С. Геометрия, 9 Н.М. Рогановский, Е.Н. Рогановская «Методика преподавания математики в средней школе. Часть 2» https://www.twirpx.com/file/1641201/ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
