Конструирование программ лаба2. Лабораторная работа №2. Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата Студентка гр. 9373
 Скачать 79.69 Kb. Скачать 79.69 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Информационные системы отчет по лабораторной работе №2 по дисциплине «Конструирование программ» Тема: Определение абсолютной и относительной погрешностей приближенных чисел. Оценка погрешностей результата
Санкт-Петербург 2021 Цель работы. Научиться определять абсолютную и относительную погрешности приближённых чисел, оценивать погрешность результата. Основные теоретические сведения. При проведении расчетов необходимо уметь практически оценивать погрешности результата. Разумная оценка погрешности позволяет удерживать оптимальное число знаков при вычислениях, оптимизируя трудоемкость расчетов. Абсолютная и относительная погрешности вычисляются непосредственно по формулам (1.2.1) и (1.2.2). Число верных знаков определяется в соответствии с теоремами 1-3 параграфа 1.2. Относительной погрешностью приближенного значения числа 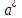 называется называется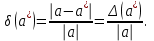 (1.2.2) (1.2.2)Эта погрешность не зависит от масштаба величины единицы измерения. Непосредственное вычисление по формулам (1.2.1) и (1.2.2) невозможно, так как 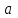 неизвестно. Часто задают величины неизвестно. Часто задают величины 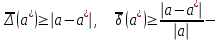 верхние границы погрешностей и полагают верхние границы погрешностей и полагают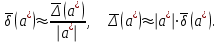 (1.2.3) (1.2.3)При записи приближенных чисел руководствуются следующими правилами. Пусть 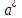 задано в виде конечной десятичной дроби задано в виде конечной десятичной дроби 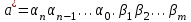 . .Значащими цифрами числа 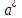 называются все цифры в его записи, начиная с первой ненулевой слева. Например, называются все цифры в его записи, начиная с первой ненулевой слева. Например,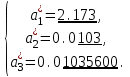 все значащие цифры подчеркнуты. все значащие цифры подчеркнуты.Значащую цифру числа 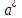 называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре. называют верной, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего этой цифре.Экспериментальные данные. 16 вариант 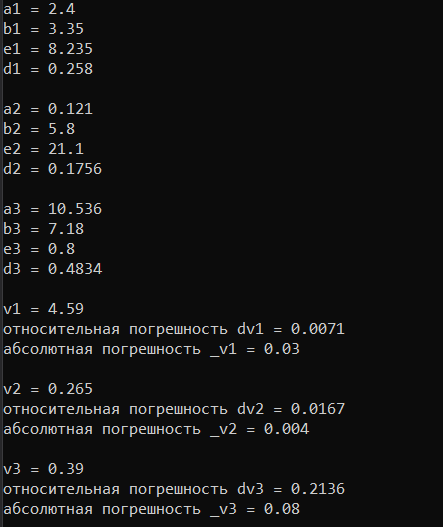 Обработка результатов. Найти абсолютную погрешность вычисления функции при заданных значениях аргументов. 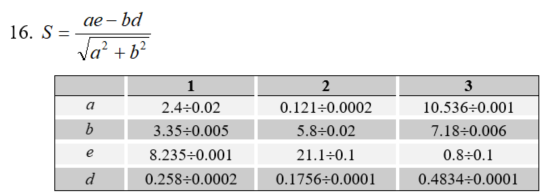 Вывод. Программа была выполнена на языке программирования C++. Мы научились определять абсолютную и относительную погрешность приближённых чисел, оценивать погрешность результата. Приложение 1 Код программы #include #include using namespace std; double func(double a, double b, double e, double d) { return ((a*e-b*d)/sqrt(a*a+b*b)); } double rnd(double num) { double rnd = 1; if (num >= 10) do { num /= 10; rnd /= 10; } while (num >= 10); else if (num < 1) { do { num *= 10; rnd *= 10; } while (num < 1); } return rnd; } int main() { setlocale(LC_ALL, "ru"); double a1(2.4), b1(3.35), e1(8.235), d1(0.258), _a1(0.02), _b1(0.005), _e1(0.001), _d1(0.0002), a2(0.121), b2(5.8), e2(21.1), d2(0.1756), _a2(0.0002), _b2(0.02), _e2(0.1), _d2(0.0001), a3(10.536), b3(7.18), e3(0.8), d3(0.4834), _a3(0.001), _b3(0.006), _e3(0.1), _d3(0.0001), da1, db1, de1, dd1, da2, db2, de2, dd2, da3, db3, de3, dd3, v1, dv1, _v1, v2, dv2, _v2, v3, dv3, _v3, h = 0.01, rndv; cout << "a1 = 2.4 "<< endl; cout << "b1 = 3.35 " << endl; cout << "e1 = 8.235 " << endl; cout << "d1 = 0.258 " << endl << endl; cout << "a2 = 0.121 " << endl; cout << "b2 = 5.8 " << endl; cout << "e2 = 21.1 " << endl; cout << "d2 = 0.1756 " << endl << endl; cout << "a3 = 10.536 " << endl; cout << "b3 = 7.18 " << endl; cout << "e3 = 0.8 " << endl; cout << "d3 = 0.4834 " << endl << endl; da1 = _a1 / abs(a1); db1 = _b1 / abs(b1); de1 = _e1 / abs(e1); dd1 = _d1 / abs(d1); da2 = _a2 / abs(a2); db2 = _b2 / abs(b2); de2 = _e2 / abs(e2); dd2 = _d2 / abs(d2); da3 = _a3 / abs(a3); db3 = _b3 / abs(b3); de3 = _e3 / abs(e3); dd3 = _d3 / abs(d3); v1 = func(a1, b1, e1, d1); dv1 = abs(a1) * abs((func(a1 + h, b1, e1, d1) - func(a1 - h, b1, e1, d1)) / (2 * h)) / abs(v1) * da1 + abs(b1) * abs((func(a1, b1 + h, e1, d1) - func(a1, b1 - h, e1, d1)) / (2 * h)) / abs(v1) * db1 + abs(e1) * abs((func(a1, b1, e1 + h, d1) - func(a1, b1, e1 - h, d1)) / (2 * h)) / abs(v1) * de1 + abs(d1) * abs((func(a1, b1, e1, d1 + h) - func(a1, b1, e1, d1 - h)) / (2 * h)) / abs(v1) * dd1; dv1 = round(dv1 * 10000) / 10000; _v1 = abs(v1) * dv1; rndv = rnd(_v1); _v1 = round(_v1 * rndv) / rndv; v1 = round(v1 * rndv) / rndv; cout << "v1 = " << v1 << endl; cout << "относительная погрешность dv1 = " << dv1 << endl; cout << "абсолютная погрешность _v1 = " << _v1 << endl << endl; v2 = func(a2, b2, e2, d2); dv2 = abs(a2) * abs((func(a2 + h, b2, e2, d2) - func(a2 - h, b2, e2, d2)) / (2 * h)) / abs(v2) * da2 + abs(b2) * abs((func(a2, b2 + h, e2, d2) - func(a2, b2 - h, e2, d2)) / (2 * h)) / abs(v2) * db2 + abs(e2) * abs((func(a2, b2, e2 + h, d2) - func(a2, b2, e2 - h, d2)) / (2 * h)) / abs(v2) * de2 + abs(d2) * abs((func(a2, b2, e2, d2 + h) - func(a2, b2, e2, d2 - h)) / (2 * h)) / abs(v2) * dd2; dv2 = round(dv2 * 10000) / 10000; _v2 = abs(v2) * dv2; rndv = rnd(_v2); _v2 = round(_v2 * rndv) / rndv; v2 = round(v2 * rndv) / rndv; cout << "v2 = " << v2 << endl; cout << "относительная погрешность dv2 = " << dv2 << endl; cout << "абсолютная погрешность _v2 = " << _v2 << endl << endl; v3 = func(a3, b3, e3, d3); dv3 = abs(a3) * abs((func(a3 + h, b3, e3, d3) - func(a3 - h, b3, e3, d3)) / (2 * h)) / abs(v3) * da3 + abs(b3) * abs((func(a3, b3 + h, e3, d3) - func(a3, b3 - h, e3, d3)) / (2 * h)) / abs(v3) * db3 + abs(e3) * abs((func(a3, b3, e3 + h, d3) - func(a3, b3, e3 - h, d3)) / (2 * h)) / abs(v3) * de3 + abs(d3) * abs((func(a3, b3, e3, d3 + h) - func(a3, b3, e3, d3 - h)) / (2 * h)) / abs(v3) * dd3; dv3 = round(dv3 * 10000) / 10000; _v3 = abs(v3) * dv3; rndv = rnd(_v3); _v3 = round(_v3 * rndv) / rndv; v3 = round(v3 * rndv) / rndv; cout << "v3 = " << v3 << endl; cout << "относительная погрешность dv3 = " << dv3 << endl; cout << "абсолютная погрешность _v3 = " << _v3 << endl << endl; return 0; } |
