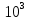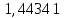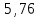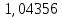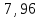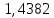распределение больцмана. Определение числа авогадро методом перрена
 Скачать 2.19 Mb. Скачать 2.19 Mb.
|
|
ОПРЕДЕЛЕНИЕ ЧИСЛА АВОГАДРО МЕТОДОМ ПЕРРЕНА Вариант 11
(компьютерная лабораторная работа) ВЫПОЛНЕНИЕ РАБОТЫ Задание №1: Изучить, на примере распределения Больцмана, зависимость проявления статистического закона от числа частиц. Введите заданные преподавателем значения температуры T и массы молекул m0. Введите число молекул N=10 нажмите кнопку «Построить». Для этана C2H6 N=10: 1 гистограмма 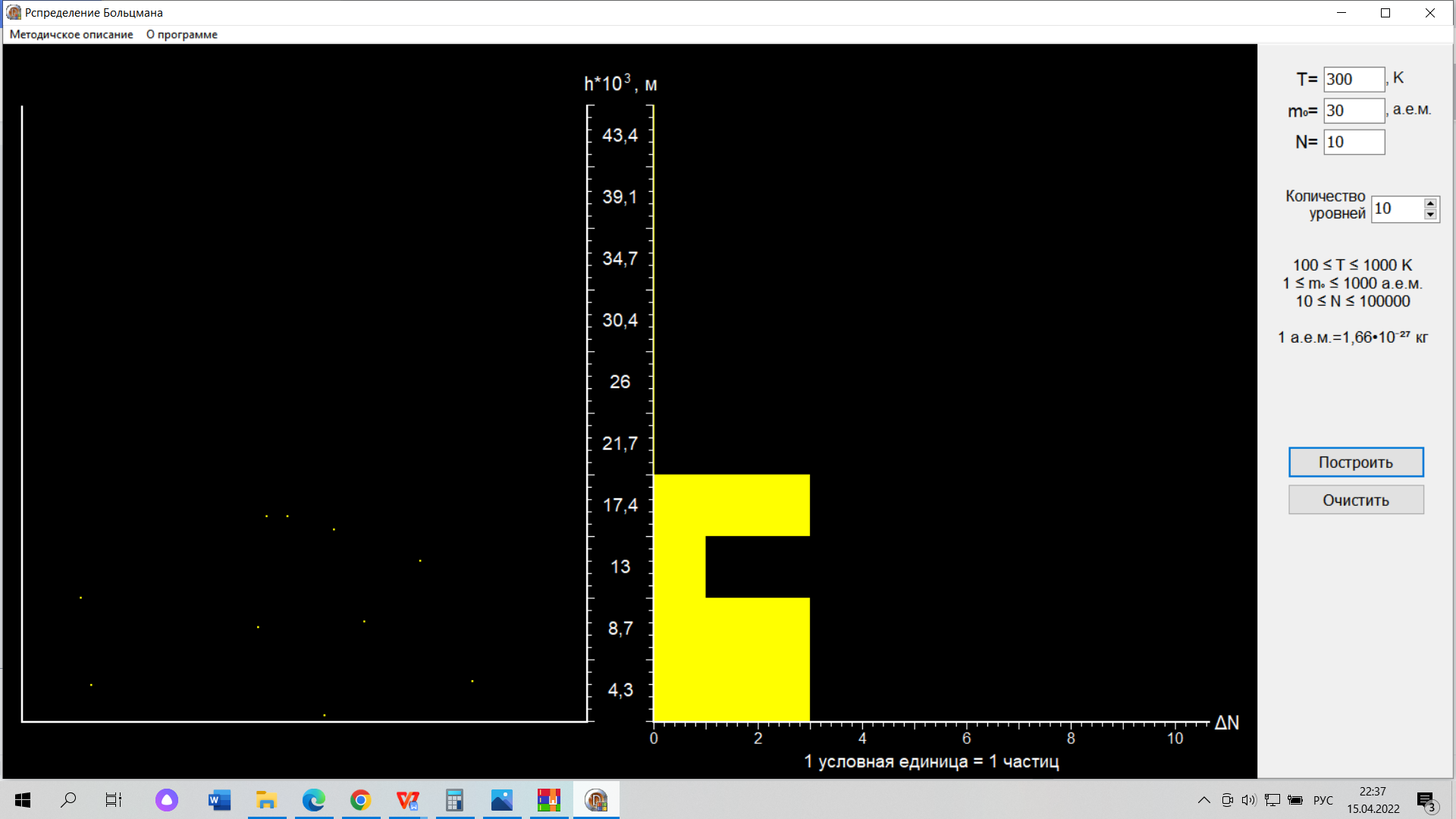 Зарисуйте в свой отчёт гистограмму распределения молекул по высоте. Не изменяя никаких параметров нажмите кнопку «Построить» и зарисуйте вторую гистограмму, затем проделайте эту процедуру третий раз и зарисуйте третью гистограмму. 2 гистограмма 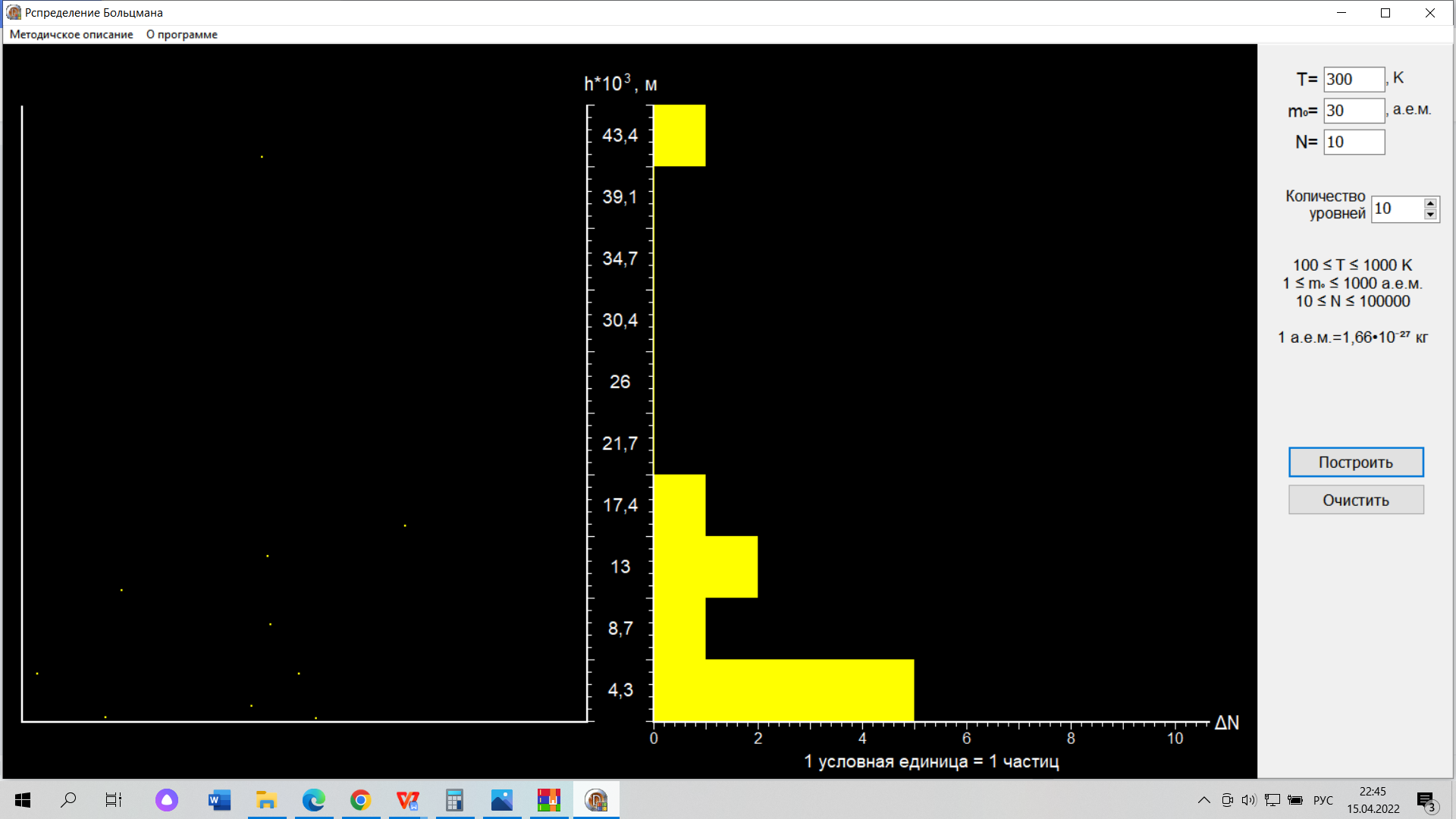 3 гистограмма  Проанализируйте Ваши рисунки и сделайте вывод: проявляется ли в этих гистограммах какая-либо закономерность. Вывод: при малом числе молекул распределение Больцмана не имеет чётких очертаний и определяется случайно. Затем, увеличивая каждый раз число молекул на порядок, пронаблюдайте, как изменяется гистограмма при изменении числа молекул от 10 до 100000. Сделайте вывод. Для этана C2H6 N = 100: Для этана C2H6 N = 1000: 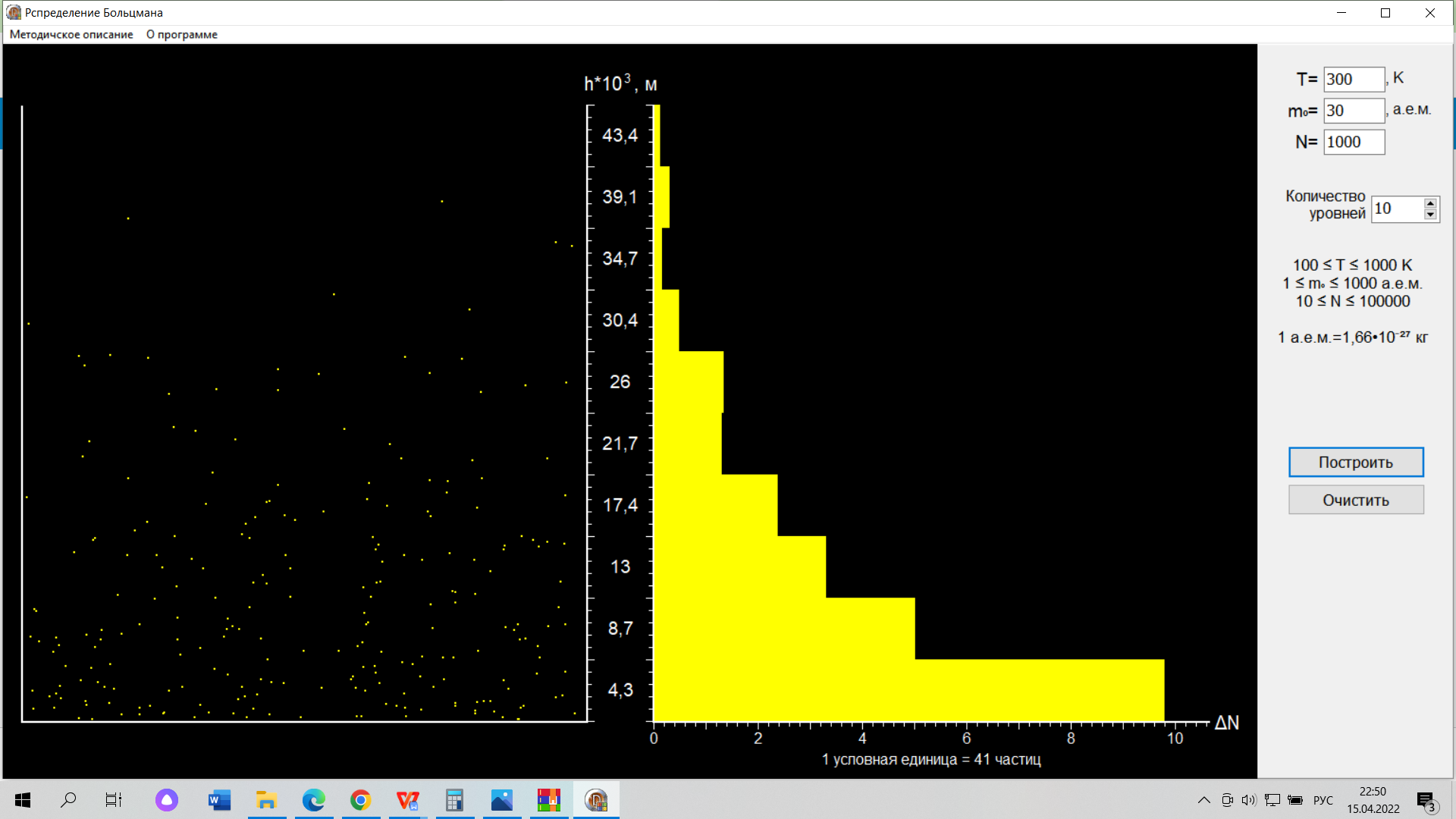 Для этана C2H6 N = 10000: Вывод: С увеличением числа молекул кривая распределения приобретает при больших числах наиболее ярко выраженный экспоненциальный характер. Задание №2: При постоянной массе молекул изучитьвлияние температуры на распределение Больцмана Т = 300 К 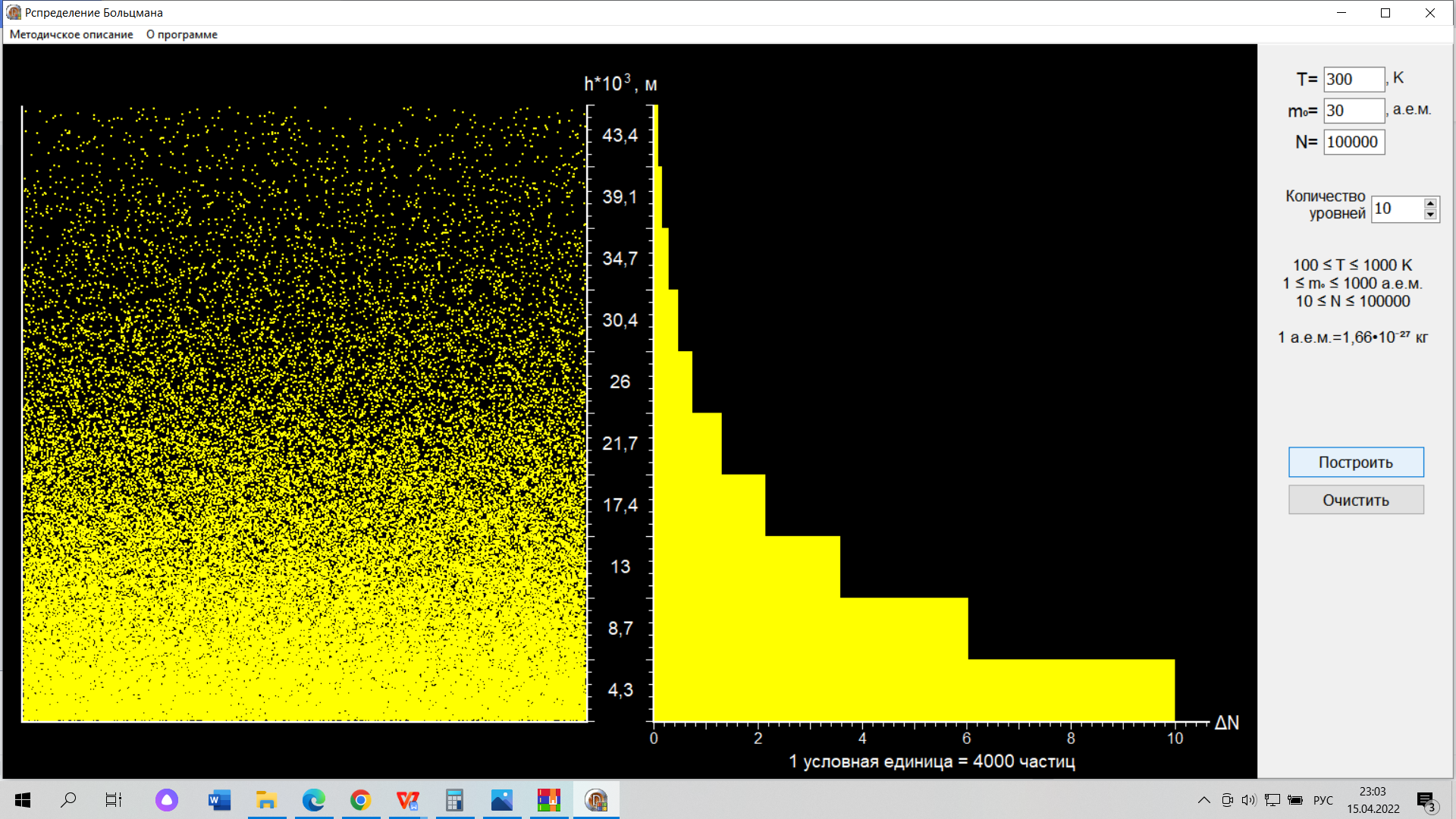 Т = 600 К 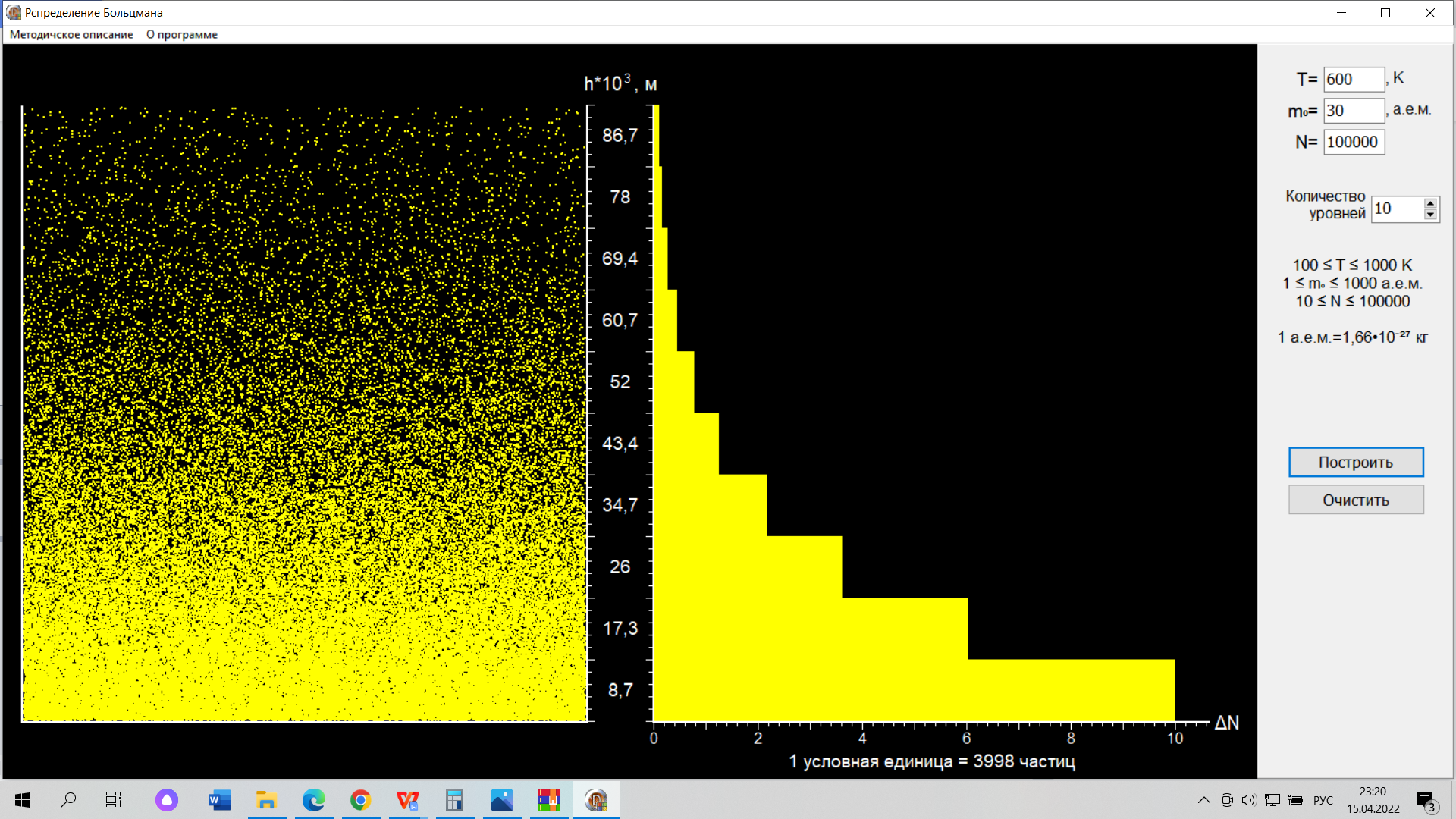 Таблица 1
Запишите в строку 1 таблицы 1 исходные значения температуры и массы молекулы. Введите их в программу, при N = 100000. Выберите слой молекул на гистограмме и направьте на него курсор мышки, этот слой выделится. Определите высоту середины слоя h1 и 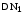 - число молекул в слое. Запишите их в таблицу. - число молекул в слое. Запишите их в таблицу.3. Выберите второй слой с высотой h2> h1. Определите и запишите в таблицу h2 и  . .4. Увеличьте температуру примерно в 1,5-2 раза и проделайте действия пунктов 2. и 3. для увеличенной температуры. Результаты запишите в таблицу. Обратите внимание на изменения в гистограмме. 5. Запишите в отчёт вывод о влиянии температуры на распределение Больцмана. Вывод: увеличение температуры приводит к увеличению высоты столбца в гистограмме во столько раз, во сколько увеличилась температура. Задание №3: При постоянной температуре изучить влияние массы молекулы на распределение Больцмана Таблица 2
Запишите в строку 1 таблицы 1 исходные значения температуры и массы молекулы. Введите их в программу, при N = 100000. Перепишите в первую строку таблицы 2 первую строку таблицы 1. Измените массу молекулы, информацию гистограммы запишите во вторую строку таблицы. Обратите внимание на изменения в гисто- грамме. Запишите в отчёт вывод о влиянии массы молекулы на распределение Больцмана. Для бутана C4H10 N = 100000 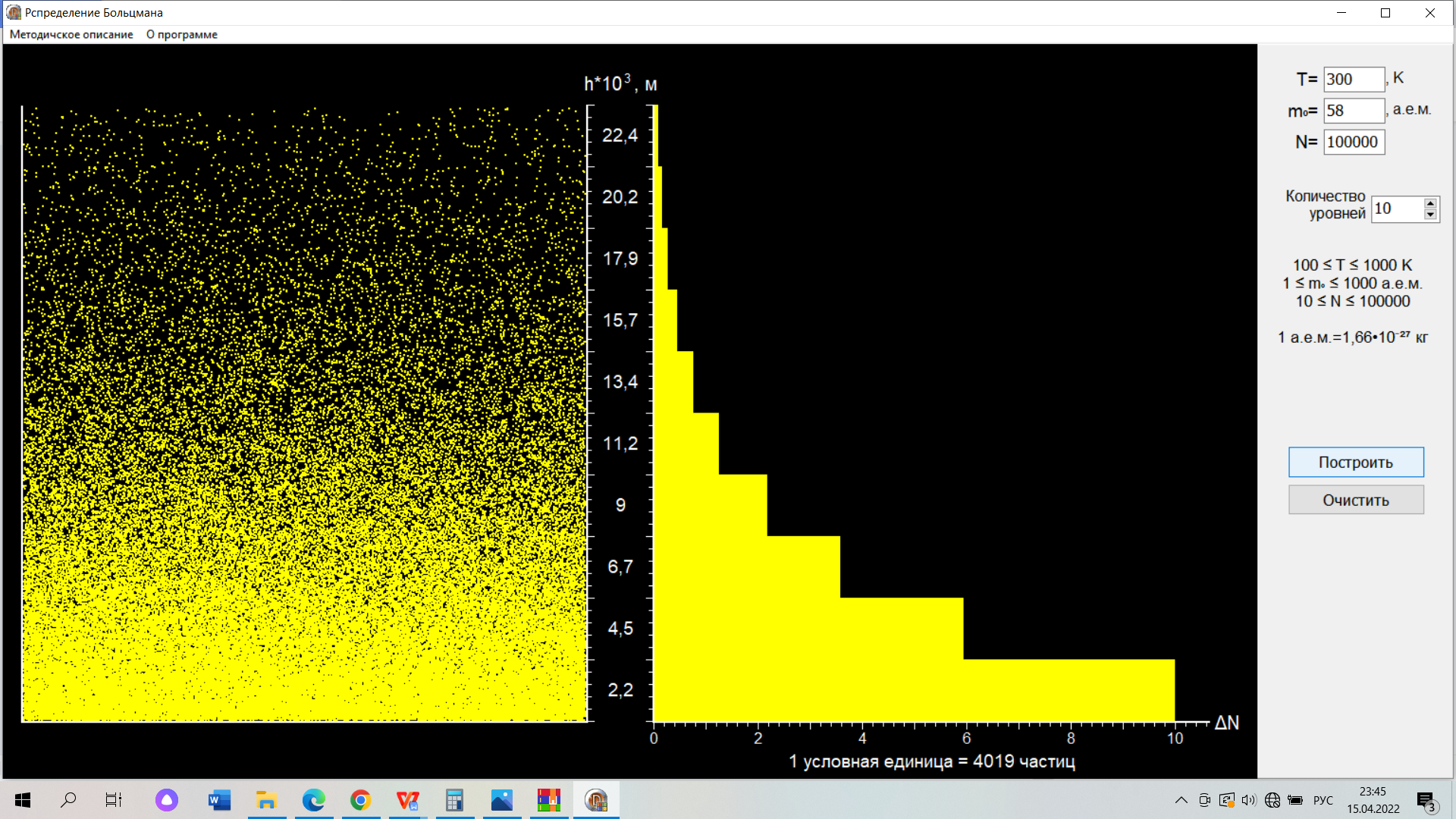 Вывод: увеличение массы молекулы приводит к уменьшению высоты столбца в гистограмме. Задание №4: Определить по результатам таблиц 1 и 2 среднее значение числа Авогадро. По формулам (2) и (3) на основе экспериментальных результатов таблиц 1 и 2 определите постоянную Больцмана и число Авогадро, результаты занесите в таблицы. Найдите среднее экспериментальное значение числа Авогадро:. Сравните Ваш результат с табличным значением числа Авогадро, найдите абсолютную погрешность,затем – относительную погрешность. Сделайте вывод и запишите его в отчёт. Выполнение задания 4: Основные расчётные формулы: Постоянная Больцмана: 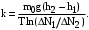 Число Авогадро: 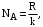 где R = 8,31 где R = 8,31 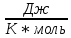 – универсальная газовая постоянная. – универсальная газовая постоянная.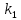 = = 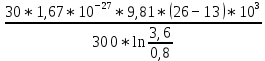 = 1,44341 * = 1,44341 * 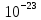 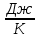 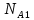 = = 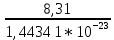 = 5,76 * = 5,76 * 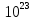 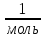 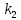 = = 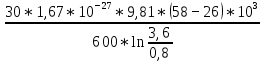 = 1,04356 * = 1,04356 * 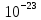 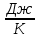 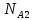 = = 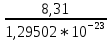 = 7,96 * = 7,96 * 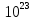 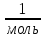 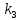 = = 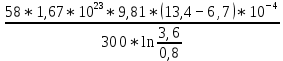 = 1,43823 * = 1,43823 * 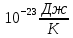 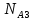 = = 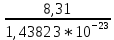 = 5,77 * = 5,77 * 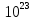 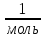 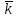 = = 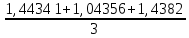 * * 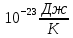 = 1,3084 * = 1,3084 * 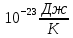 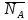 = = 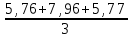 * * 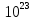 = 6,50 * = 6,50 * 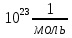 . .Табличные значения постоянной Больцмана и числа Авогадро: k = 1,38065 * 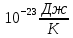 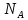 = 6,02 * = 6,02 * 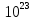 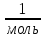 . .Абсолютная погрешность: 𝞓k = |1,38065 – 1,3084| * 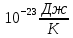 = 0,07225 * = 0,07225 * 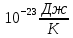 𝞓 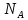 = |6,50 – 6,02| * = |6,50 – 6,02| * 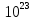 = 0,48 * = 0,48 * 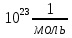 . .Относительная погрешность: εk = 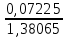 * 100 % = 5 % * 100 % = 5 %εk = 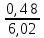 * 100 % = 8 % * 100 % = 8 %Вывод: Рассчитанные на основании экспериментальных данных постоянная Больцмана и число Авогадро нсколько отличаются от табличных. Ошибка составляет 5 и 8 % соответственно. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||