. Задавая давление при, . Поделим на число Авогадро, где. Распределение Больцмана
 Скачать 2.16 Mb. Скачать 2.16 Mb.
|
|
Билет 1 Барометрическая формула. Позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту. Пусть идеальный газ находится во внешнем поле силы тяжести. Рассмотрим равновесие малого объёма газа:  => =>  ; где ; где 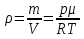 => => 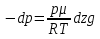 => => 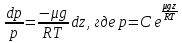 . Задавая давление при . Задавая давление при 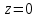 , ,  => => 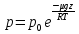 . Поделим на число Авогадро: . Поделим на число Авогадро: 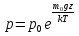 , где , где 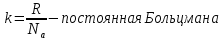 . .  Распределение Больцмана. 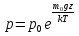 но, но,  => => 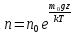 , но , но  , тогда: , тогда: 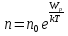 – распр. Больцмана. – распр. Больцмана.Определение а.е.м. Углеродная единица — внесистемная единица массы, применяемая для масс молекул, атомов, атомных ядер и элементарных частиц. Атомная единица массы выражается через массу нуклида углерода 12С и равна 1/12 массы этого нуклида.  Билет 2 Неравенство Клаузиуса. Суммарное количество приведённой теплоты в любом замкн. цикле для люой ТермСист не может быть больше нуля: 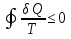 , где , где  - кол-во теплоты, сообщаемое системе (или отводимое от неё: - кол-во теплоты, сообщаемое системе (или отводимое от неё: 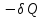 ) на бесконечно малом участке цикла; Т - абс. темп-pa соответств. элемента среды; ) на бесконечно малом участке цикла; Т - абс. темп-pa соответств. элемента среды; 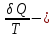 элементарная приведённая теплота. Необратимому (хотя бы на одном участке) циклу соответствует неравенство, циклу, состоящему только из обратимых процессов,- знак равенства (равенство Клаузиуса). Зависит только от начального и конечного состояний. элементарная приведённая теплота. Необратимому (хотя бы на одном участке) циклу соответствует неравенство, циклу, состоящему только из обратимых процессов,- знак равенства (равенство Клаузиуса). Зависит только от начального и конечного состояний.Термодинамическая энтропия. Мера необратимого рассеяния энергии.  (диф форма), (диф форма), 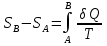 (интегр форма), где (интегр форма), где 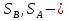 энтропия конечного и начального состояния. энтропия конечного и начального состояния.Второе начало термодинамики. По Клазиусу: - теплота сама по себе, без изменения в окружающих телах не может перейти от менее нагретого тела к более нагретому. По Томсону: в природе невозможен круговой процесс, единственным результатом которого была бы механическая работа, совершаемая за счёт отвода теплоты от теплового резервуара. Теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе (рассеиванием энергии). Относительная атомная масса. (сокращенно – атомная масса). Есть отношение массы его атома к 1/12 части массы атома 12С (углерод).  Билет 3 Первое начало термодинамики. Изменение внутренней энергии термодинамической системы (тела) может быть осуществлено 'двумя путями: путём совершения механической работы и путём теплопередачи. 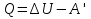 , где , где 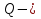 количество теплоты переданное системе, количество теплоты переданное системе, 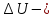 изменение внутренней энергии системы, изменение внутренней энергии системы,  работа совершённая над системой. работа совершённая над системой. 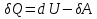 . Первое начало запрещает существование вечного двигателя без подвода внешней энергии. . Первое начало запрещает существование вечного двигателя без подвода внешней энергии.Определение интервала событий в СТО. Это есть:  , где: , где: 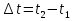 , , 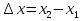 , , 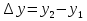 , ,  - разности времён и координат двух событий. Т.е это расстояние между двумя событиями в пространстве времени, являющиеся обобщением евклидова пространства между двумя точками. - разности времён и координат двух событий. Т.е это расстояние между двумя событиями в пространстве времени, являющиеся обобщением евклидова пространства между двумя точками. Билет 4 Адиабатический процесс. Процесс, при котором отсутствует теплообмен (  ) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. ) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы.Из первого начала термодинамики:  , т. е. внешняя работа совершается за счет изменения внутренней энергии системы. , т. е. внешняя работа совершается за счет изменения внутренней энергии системы.  . .Уравнение Пуассона. Запишем:  -первое начало термодин. -первое начало термодин. – ур. Менделеева-Клап. – ур. Менделеева-Клап.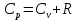 – ур. Майера – ур. МайераПроведя преобразования (выразим dT из 2го, подставим в первое, так же из третьего R во первое), получим: 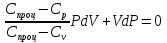 – уравнение некоторого политропического процесса. Для адиабаты ( – уравнение некоторого политропического процесса. Для адиабаты (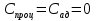 ), получим: ), получим: 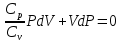 , где , где 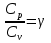 -показатель адиабаты, тогда проинтегрируем -показатель адиабаты, тогда проинтегрируем 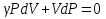 : :  - уравнение Пуассона. - уравнение Пуассона. Уравнение адиабаты в Р-Т координатах. При помощи ур. Менд-Клап исключим из  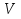 : :  Определение относительной молекулярной массы молекулы. Это есть отношение массы молекулы вещества к 1/12 части массы атома 12С (углерод).  Билет 5. Распределение Максвелла Распределение по скоростям (или импульсам) молекул системы, находящейся в состоянии термодинамического равновесия. Предполагая, что некоторое кол-во молекул будут иметь некоторую скорость а доля быстрых и медленных молекул не велика, можно определить какая доля молекул 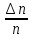 имеет скорость заключённую в опр. интервале имеет скорость заключённую в опр. интервале  : : Экспериментальная проверка закона распределения Максвелла  Опыт Эстермана. Пучок атомов цезия вылетал из печи через отверстие 1, под действием силы тяжести двигался па параболе. Некоторые траектории движения проходили через щель 2, после улавливались детектором 3, с меняющейся высотой h, где h зависела от скорости атомов. Т е детектор считал сколько атомов пролетало в щель (а пролетали только те, что имели определённую скорость) Так было получено распределение скоростей атомов Цезия. Они подтвердили формулу Максвелла. Определение волнового числа Количество волн в одном сантиметре; численно равно числу периодов волны, укладывающихся в отрезок 2π метров. Это пространственный аналог круговой частоты; определяет пространственный период и направление распространения волны. 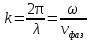 Определение волнового вектора 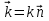 , где , где 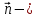 единичный вектор, направленный перпендикулярно волновой поверхности, в сторону распространения волны. единичный вектор, направленный перпендикулярно волновой поверхности, в сторону распространения волны.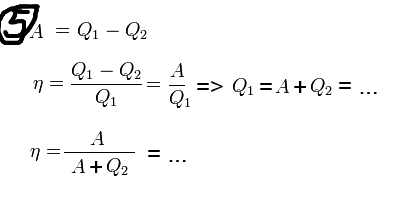 Билет 6 Статистическое обоснование второго начала термодинамики. Пусть в сосуде находятся шесть молекул газа. Мысленно разделим сосуд на три равные части. Хаотически перемещаясь, молекулы создают определенные макрораспределения. В теоретической физике доказывается, что термодинамическая вероятность, т. е. число N частиц по п состояниям (шесть частиц в трех частях сосуда), определяется формулой 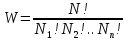 Наибольшая термодинамическая вероятность у равномерного распределения, оно может осуществляться наибольшим числом способов. Все процессы в природе протекают в направленна, приводящем к увеличению вероятности состояния Формула Больцмана для статистической энтропии. Связь энтропии с термодинамической вероятностью установил Больцман — энтропия пропорциональна логарифму термодинамической вероятности:  . Статистический смысл понятия энтропии состоит в том, что увеличение энтропии изолированной системы связано с переходом этой системы из менее вероятного состояния в более вероятное. . Статистический смысл понятия энтропии состоит в том, что увеличение энтропии изолированной системы связано с переходом этой системы из менее вероятного состояния в более вероятное.Определение уравнения состояния вещества. Описывает зависимость между термодинамическими (макроскопическими) параметрами системы (давление, объём, температура).  , где , где 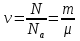  Билет 7 Закон возрастания энтропии. «В изолированной системе энтропия не уменьшается». Если в некоторый момент времени замкнутая система находится в неравновесном макроскопическом состоянии, то в последующие моменты времени наиболее вероятным следствием будет монотонное возрастание ее энтропии. Если в некоторый момент времени энтропия замкнутой системы отлична от максимальной, то в последующие моменты энтропия не убывает — увеличивается или в предельном случае остается постоянной. Рассмотрим теплообмен между двумя частями системы A1 и A2, имеющими температуры T1 и T2. Пусть T1 При этом энтропия тела A1 изменится на величину ΔQ1/T1 , а энтропия тела A2 – на величину ΔQ2/T2 . Общее изменение энтропии системы: 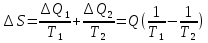 Поскольку T1 Третье начало термодинамики Справедлива только для равновесных систем. При стремлении системы к абсолютному нулю, её энтропия стремится к константе, принимаемой за ноль. Теплоёмкость тоже стремится к нулю. Следствия: невозможно достичь состояния с абсолютным нулём; ур. Менд-Клап. неприменимо для описания идеального газа при 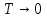 Определение идеального газа. Математическая модель газа, в которой предполагается, что: 1) потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объем молекул газа пренебрежимо мал. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.  Билет 8 Цикл Карно. Замкнутый цикл. Для возникновения теплопередачи необходима разность температур. 1-2-изотермический проц.: газ получает тепло (  ) от нагревателя, расширяясь при постоянной температуре ) от нагревателя, расширяясь при постоянной температуре  . .2-3-адиабатический: газ расширяется без теплообмена 3-4-изотермический: газ отдаёт тепло холодильнику (холодильник забирает  ), сжимается при постоянной температуре ), сжимается при постоянной температуре 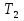 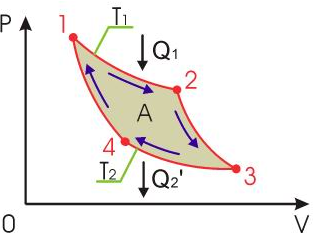 4-1-адиабатический: газ сжимается без теплообмена. КПД идеальной тепловой машины. Используя уравнение адиабаты, распишем процессы 2-3 4-1: 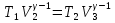 , , 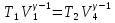 , поделим первое на второе: , поделим первое на второе:  . Поскольку процессы 1-2 и 3-4 – изотермические, то изменение внутренней энергии = 0, тогда согласно первому началу термодинамики и работе изотермического процесса ( . Поскольку процессы 1-2 и 3-4 – изотермические, то изменение внутренней энергии = 0, тогда согласно первому началу термодинамики и работе изотермического процесса ( ), получим: ), получим: 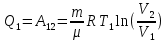 , , 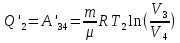 . Используем формулу кпд: . Используем формулу кпд: 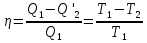 Теорема Карно.
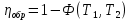
 Определение средней кинетической энергии атома.  Кинетическая энергия поступательного движения атомов и молекул, усредненная по огромному числу беспорядочно движущихся частиц, является мерилом того, что называется температурой. Если температура T измеряется в градусах Кельвина (К), то связь ее с  дается соотношением: дается соотношением: Билет 9 Неравенство Клаузиуса. Суммарное количество приведённой теплоты в любом замкн. цикле для люой ТермСист не может быть больше нуля: 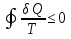 , где , где  - кол-во теплоты, сообщаемое системе (или отводимое от неё: - кол-во теплоты, сообщаемое системе (или отводимое от неё: 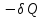 ) на бесконечно малом участке цикла; Т - абс. темп-pa соответств. элемента среды; ) на бесконечно малом участке цикла; Т - абс. темп-pa соответств. элемента среды; 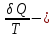 элементарная приведённая теплота. Необратимому (хотя бы на одном участке) циклу соответствует неравенство, циклу, состоящему только из обратимых процессов,- знак равенства (равенство Клаузиуса). Зависит только от начального и конечного состояний. элементарная приведённая теплота. Необратимому (хотя бы на одном участке) циклу соответствует неравенство, циклу, состоящему только из обратимых процессов,- знак равенства (равенство Клаузиуса). Зависит только от начального и конечного состояний.Термодинамическая энтропия. Мера необратимого рассеяния энергии.  (диф форма), (диф форма), 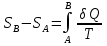 (интегр форма), где (интегр форма), где 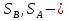 энтропия конечного и начального состояния. энтропия конечного и начального состояния.Второе начало термодинамики. По Клазиусу: - теплота сама по себе, без изменения в окружающих телах не может перейти от менее нагретого тела к более нагретому. По Томсону: в природе невозможен круговой процесс, единственным результатом которого была бы механическая работа, совершаемая за счёт отвода теплоты от теплового резервуара. Теплота не может перейти от холодного тела к горячему без каких-либо других изменений в системе (рассеиванием энергии). Определение интерференции упругих волн При интерференции (интерференция – взаимное усиление/ослабление волн при наложении оных друг на друга, приводит к перераспределению колебаний) нескольких упругих волн их распространение можно изучать по отдельности для каждой волны, пренебрегая влиянием волн друг на друга. Упругая волна – волна распространяющаяся в жидких, твёрдых, газообразных средах за счёт действия упругих сил.  Билет 10 Первое начало термодинамики в дифф и инт форме 1. В дифференциальной форме: 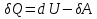 . В интегральной форме: Q=дU + А . В интегральной форме: Q=дU + АСтоячая волна — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Образуется при наложении двух волн с одинаковой амплитудой и частотой, когда волны движутся навстречу друг другу. Пучность — участок стоячей волны, в котором колебания имеют наибольшую амплитуду. Противоположностью пучности является узел — участок волны, в котором амплитуда колебаний минимальна. 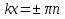 . Координаты пучностей: . Координаты пучностей: 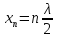 . Соседние пучности находятся на расстоянии . Соседние пучности находятся на расстоянии  Узлы – точки где 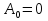 ; их можно найти из условия ; их можно найти из условия 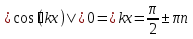 Координаты узлов: 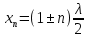 . Соседние узлы также находятся на расстоянии . Соседние узлы также находятся на расстоянии  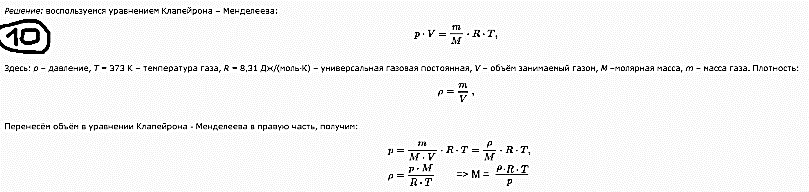 Билет 11 Цикл Карно. Замкнутый цикл. Для возникновения теплопередачи необходима разность температур. 1-2-изотермический проц.: газ получает тепло (  ) от нагревателя, расширяясь при постоянной температуре ) от нагревателя, расширяясь при постоянной температуре  . . 2-3-адиабатический: газ расширяется без теплообмена 3-4-изотермический: газ отдаёт тепло холодильнику (холодильник забирает  ), сжимается при постоянной температуре ), сжимается при постоянной температуре 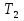 .4-1-адиабатический: газ сжимается без теплообмена. .4-1-адиабатический: газ сжимается без теплообмена.КПД идеальной тепловой машины. Используя уравнение адиабаты, распишем процессы 2-3 4-1: 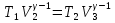 , , 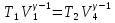 , поделим первое на второе: , поделим первое на второе:  . Поскольку процессы 1-2 и 3-4 – изотермические, то изменение внутренней энергии = 0, тогда согласно первому началу термодинамики и работе изотермического процесса ( . Поскольку процессы 1-2 и 3-4 – изотермические, то изменение внутренней энергии = 0, тогда согласно первому началу термодинамики и работе изотермического процесса ( ), получим: ), получим: 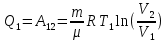 , , 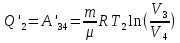 . Используем формулу кпд: . Используем формулу кпд: 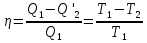 Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах. В СИ: метры. Период волны – это интервал времени между прохождением двух смежных вершин волн через фиксированную вертикаль. В СИ: секунды. Частота волны - это число полных колебаний или циклов волны, совершенных в единицу времени. В Си:герцы, с-1  Билет 12 Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид: p*V=m/M*R*T Когерентные волны - волны, характеризующиеся одинаковой частотой и постоянством разности фаз в заданной точке пространства. Когерентность волн является необходимым условием получения устойчивой интерференционной картины. Упругие волны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил. Билет 13 Уравнение стоячей волны. Стоячая волна — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. Уравнение стоячей волны: 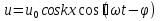 Узлы и пучности стоячей волны. Пучности – участки стоячей волны, где амплитуда колебаний максимальна. 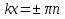 . Аналогично узлы – участки стоячей волны с минимальной амплитудой. . Аналогично узлы – участки стоячей волны с минимальной амплитудой. 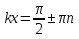 Определение Термодинамической Системы (ТС).. Термодинамическая система - это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой, энергией, веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики. Определение изолированной ТС Изолированная система (замкнутая система) — термодинамическая система, которая не обменивается с окружающей средой ни веществом, ни энергией. В термодинамике постулируется (как результат обобщения опыта), что изолированная система постепенно приходит в состояние термодинамического равновесия, из которого самопроизвольно выйти не может (нулевое начало термодинамики).  Билет 14 Поток энергии упругой волны. Поток энергии упругой волны – количество энергии, переносимое волной через некоторую поверхность в единицу времени. 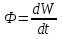 Измеряется в ваттах. Измеряется в ваттах.Вычисление потока энергии с помощью вектора Умова. Вектор Умова – вектор плотности потока. Среднее значение: 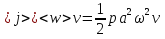 . Различен в различных точках пространства, изменяется во времени по закону квадрата синуса. . Различен в различных точках пространства, изменяется во времени по закону квадрата синуса.Определение абсолютной шкалы температур и ее связь с температурной шкалой Цельсия. Абсолютная шкала температур – мера основания нижнего предела такой шкалы составляет абсолютный 0, ниже которого температура опускаться не может. 0К соответствует -273  Соответственно, температура замерзания воды в Кельвинах составляет 273 градуса, а кипения – 373К. 1 Соответственно, температура замерзания воды в Кельвинах составляет 273 градуса, а кипения – 373К. 1  Билет 15 Статистическое описание равновесных состояний. Статистический метод описания состояний макроскопических тел (термодинамических систем) основывается на определении статистических закономерностей случайного (теплового) движения отдельных микрочастиц тела. Изменение их средних значений происходит закономерно. Наблюдаемые параметры термодинамической системы (температура, давление и т.д.) определяются как средние значения соответствующих функций от переменных, описывающих движение микрочастиц. Разработкой методов определения свойств макроскопических тел через параметры, описывающие движение и взаимодействие микрочастиц, из которых эти тела состоят, занимается статистическая физика. Распределение Больцмана. Распределение Больцмана - распределение по энергиям частиц (атомов, молекул) идеального газа в условиях термодинамического равновесия, 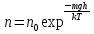 . .Принцип относительности Галилея. Принцип физического равноправия инерциальных систем отсчёта в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы. Отсюда следует, что никакими механическими опытами, проводящимися в какой-либо инерциальной системе, нельзя определить, покоится ли данная система или движется равномерно и прямолинейно. Преобразования Галилея. Преобразование при коллинеарных осях: x’ = x + ut; y’ = y; z’ = z; t’ = t; v’ = v + u  (вектора) a’ = a; (вектора) (вектора) a’ = a; (вектора) Билет 16 Фазовое пространство. Фазовое пространство – пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства. Распределение Максвелла-Больцмана. Распределение Максвелла-Больцмана показывает зависимость концентрации молекул от их координат. 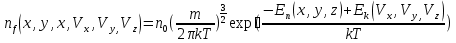 Кинетическая энергия частицы в СТО.   Билет 17 Политропический процесс в идеальном газе. Политропический процесс – процесс, происходящий при постоянной теплоемкости. К таким относятся адиабатический, изохорный, изобарический и изотермический процессы. Уравнение политропы:  Теплоемкость и работа в политропическом процессе. Работа в политропическом процессе: 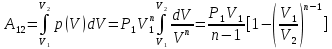 Теплоемкость: Если процесс изотермический, С -> ∞ Изобарический: С =  Изохорный: (С - Изохорный: (С - 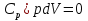 Адиабатный: C = 0 Адиабатный: C = 0Определение молярной массы. Единицы в СИ Молярная масса – масса одного моль вещества. Для определения молярной массы соединения нужно сложить молярные массы всех входящих в него элементов. Измеряется в кг\моль 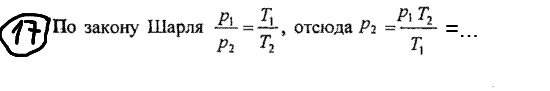 Билет 18 Связь между импульсом и энергией релятивистской частицы. 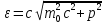 ; ;  . .Определение тепловой машины. Тепловая машина — устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник). Преобразование осуществляется за счёт изменения внутренней энергии рабочего тела — на практике обычно пара или газа. КПД тепловой машины. КПД машины: 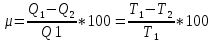  Билет 19 Сферические упругие волны Сферические упругие волны возбуждаются точечным источником, размеры которого малы по сравнению с расстоянием до рассматриваемых точек. Отличие сферической волны от плоской. При распространении сферической волны ее волновые поверхности (геометрическое место точек среды, в которых фаза волны в рассматриваемый момент времени имеет одно и то же значение) представляют собой систему концентрических сфер. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей. Определение адиабатически изолированной системы. Адиабатически изолированная система — термодинамическая система, которая не обменивается с окружающей средой энергией в форме теплоты. Изменение внутренней энергии такой системы равно производимой над ней работе. Всякий процесс в адиабатически изолированной системе называется адиабатическим процессом. 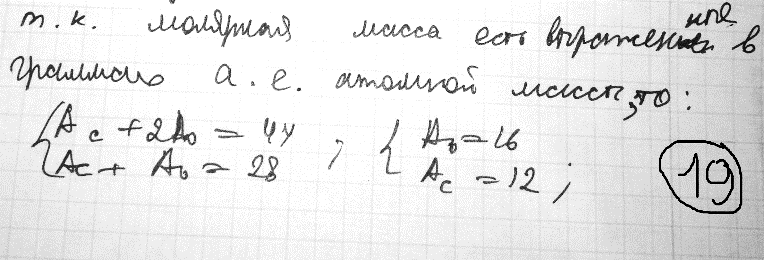 Билет 20 Специальная теория относительности. Специальная теория относительности — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. Постулаты Эйнштейна: Постулат 1 (принцип относительности Эйнштейна). Любое физическое явление протекает одинаково во всех инерциальных системах отсчёта. Постулат 2 (принцип постоянства скорости света). Скорость света в «покоящейся» системе отсчёта не зависит от скорости источника. Скорость света одинакова во всех инерциальных системах. Преобразования Лоренца: Общий вид преобразований Лоренца в векторном виде, когда скорость систем отсчёта имеет произвольное направление:   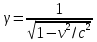 - фактор Лоренца - фактор ЛоренцаОпределение молярной теплоемкости газа при изохорном процессе Теплоёмкость идеального газа — отношение количества теплоты, сообщённого газу, к изменению температуры δТ, которое при этом произошло. Определение молярной теплоемкости при изохорном процессе: 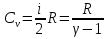  Билет 21 Количество степеней свободы (i) тела- минимальное количество координат, которые надо задать для однозначного определения положения тела. Для одноатомного газа i=3. Т.к. молекула может двигаться поступательно в трех направлениях (по координатам(x, y, z)) Для двухатомного газа i=5. Т.к. молекула может двигаться поступательно в 3х направлениях + 2 вращательных движений вокруг осей. Для трехатомного и более газа i=6. Т.к. молекула может двигаться поступательно в 3х направлениях + 3 вращательных движений вокруг осей Закон равномерного распределения энергии по степеням свободы Средняя кин. энергия приходящаяся на одну степень свободы при тепловом движении 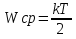 тогда полная энергия: тогда полная энергия: 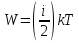 . А суммарная кин. энергия будет иметь вид: . А суммарная кин. энергия будет иметь вид: 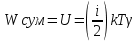 (γ-количество вещества) (γ-количество вещества)Релятивистский множитель  . Множитель показывает во сколько раз возрастает масса тела движущейся релятивистской частицы, или замедляется течение ее времени. Используется в преобразованиях Лоренца. . Множитель показывает во сколько раз возрастает масса тела движущейся релятивистской частицы, или замедляется течение ее времени. Используется в преобразованиях Лоренца. Билет 22 Адиабатический процесс. Процесс, при котором отсутствует теплообмен (  ) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы. ) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы.Из первого начала термодинамики:  , т. е. внешняя работа совершается за счет изменения внутренней энергии системы. , т. е. внешняя работа совершается за счет изменения внутренней энергии системы.  . .Уравнение Пуассона. Запишем:  -первое начало термодин. -первое начало термодин. – ур. Менделеева-Клап. – ур. Менделеева-Клап.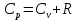 – ур. Майера – ур. МайераПроведя преобразования (выразим dT из 2го, подставим в первое, так же из третьего R во первое), получим: 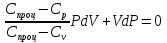 – уравнение некоторого политропического процесса. Для адиабаты ( – уравнение некоторого политропического процесса. Для адиабаты (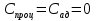 ), получим: ), получим: 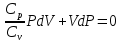 , где , где 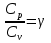 -показатель адиабаты, тогда проинтегрируем -показатель адиабаты, тогда проинтегрируем 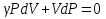 : :  - уравнение Пуассона. - уравнение Пуассона. Уравнение адиабаты в Р-Т координатах. При помощи ур. Менд-Клап исключим из   : :  Определение средней квадратичной скорости атома  ; ;  ; ;  ; ;  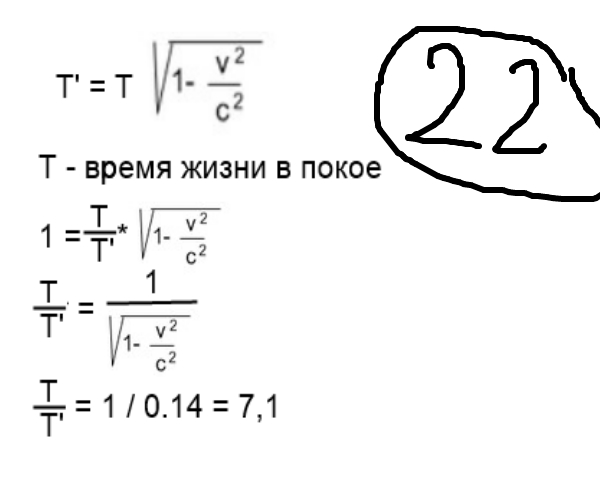 Билет 23 Первое начало термодинамики. Изменение внутренней энергии термодинамической системы (тела) может быть осуществлено 'двумя путями: путём совершения механической работы и путём теплопередачи. 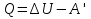 , где , где 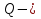 количество теплоты переданное системе, количество теплоты переданное системе, 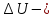 изменение внутренней энергии системы, изменение внутренней энергии системы,  работа совершённая над системой. работа совершённая над системой. 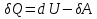 . Первое начало запрещает существование вечного двигателя без подвода внешней энергии. . Первое начало запрещает существование вечного двигателя без подвода внешней энергии.Определение числа степеней свободы Количество степеней свободы (i) тела- минимальное количество координат, которые надо задать для однозначного определения положения тела. Для одноатомного газа i=3. Т.к. молекула может двигаться поступательно в трех направлениях (по координатам(x, y, z)) Для двухатомного газа i=5. Т.к. молекула может двигаться поступательно в 3х направлениях + 2 вращательных движений вокруг осей. Для трехатомного и более газа i=6. Т.к. молекула может двигаться поступательно в 3х направлениях + 3 вращательных движений вокруг осей.  Билет 24 Основное уравнение МКТ Давление газа на стенки сосуда пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы. 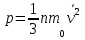 Иные формулировки:  ; ; 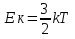 => => 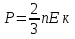 Холодильная машина Холодильные машины- машины позволяющие охлаждать различные тела за счет совершения работы. Эффективность таких тепловых машин характеризуют холодильный коэффициент: 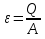 , где , где  — тепло, отбираемое от холодного конца (в холодильных машинах) или передаваемое к горячему (в тепловых насосах); — тепло, отбираемое от холодного конца (в холодильных машинах) или передаваемое к горячему (в тепловых насосах); 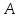 — затрачиваемая на этот процесс работа (или электроэнергия). Наилучшими показателями производительности для таких машин обладает обратный цикл Карно: в нём холодильный коэффициент — затрачиваемая на этот процесс работа (или электроэнергия). Наилучшими показателями производительности для таких машин обладает обратный цикл Карно: в нём холодильный коэффициент 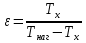  Билет 25 Билет 25Рассмотрим выделенный участок стержня длиной Δx . При колебаниях скорость этого участка будет 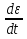 и величина деформации и величина деформации  => => 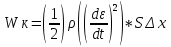 ; ;  Объемная плотность механической энергии: 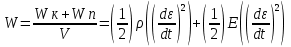 Если для волны, то:  Среднее значение плотности потока энергии, переносимой волной:  Обратимый термодинамический процесс- процесс, при котором при изменении параметров состояния в первоначальные, окружающие тела также переходят в первоначальное состояние.  Билет 26 Вектор Умова: 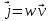 где w – объемная плотность энергии. Среднее значение: где w – объемная плотность энергии. Среднее значение: 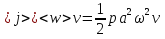 . Различен в различных точках пространства, изменяется во времени по закону квадрата синуса. . Различен в различных точках пространства, изменяется во времени по закону квадрата синуса.Поток энергии – количество энергии, переносимое через некоторую произвольную поверхность в единицу времени: 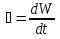 где W – количество энергии где W – количество энергии 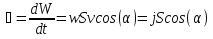 где S – площадь этой поверхности где S – площадь этой поверхностиНеобратимый термодинамический процесс – процесс, при котором термодинамическая система, выведенная из состояния термодинамического равновесия, при проведении данного процесса в обратом направлении не повторяет всех положений прямого процесса 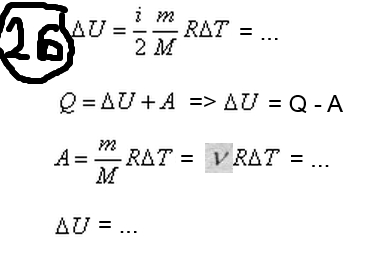 Билет 27 Если возвращающая сила пропорциональна смещению точки, то такая волна называется упругой Одномерное волновое уравнение: 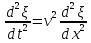 . Общее решение: . Общее решение: 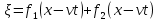  – описывает возмущение, распространяющееся в положительном направлении оси X – убегающую волну – описывает возмущение, распространяющееся в положительном направлении оси X – убегающую волну 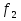 – описывает возмущение, распространяющееся в отрицательном направлении оси X – набегающую волну – описывает возмущение, распространяющееся в отрицательном направлении оси X – набегающую волнуСредняя длина свободного пробега молекул – среднее расстояние, которое пролетает молекула между двумя последовательными столкновениями с другими молекулами 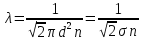 , где , где 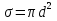 – эффективное сечение взаимодействия – эффективное сечение взаимодействия Билет 28 Основное уравнение релятивистской динамики:  Взаимосвязь массы и энергии: Взаимосвязь массы и энергии:  Значение постоянной С определяем из условия равенства нулю кинетической энергии при нулевой скорости: 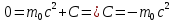 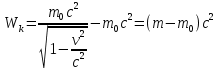 Определение молярной теплоемкости идеального газа при изобарном процессе: 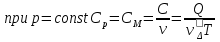 ; ;   ; ;Значит: 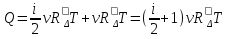 . Подставим в 1 формулу: . Подставим в 1 формулу: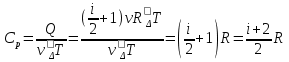  Билет 29 Стоячая волна образуется при наложении двух волн одинаковой частоты, бегущих в противоположных направлениях. Уравнение:  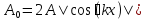 - амплитуда стоячей волны - амплитуда стоячей волныПучности – точки где 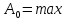 ; их можно найти из условия ; их можно найти из условия 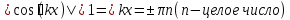 Координаты пучностей: Координаты пучностей: 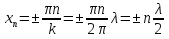 Соседние пучности находятся на расстоянии Соседние пучности находятся на расстоянии  Узлы – точки где 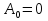 ; их можно найти из условия ; их можно найти из условия 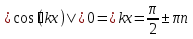 Координаты узлов:  . Соседние узлы также находятся на расстоянии . Соседние узлы также находятся на расстоянии  Внутренняя энергия идеального газа – суммарная кинетическая энергия всех молекул газа 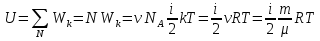  Билет 30 Принцип относительности Галилея: Если в двух замкнутых лабораториях, одна из которых движется равномерно и прямолинейно (и поступательно) относительно другой, провести одинаковый механический эксперимент, то результат будет одинаковым. При переходе от одной системе отсчета к другой: 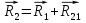 где где  - вектор, задающий положение одной системы относительно другой - вектор, задающий положение одной системы относительно другой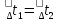 т.к. масштаб времени не меняется: т.к. масштаб времени не меняется:  ; ; 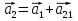 . Выберем класс инерциальных систем отсчета. Эти системы могут двигаться с разными скоростями, но их относительные ускорения нулевые, поэтому при переходе от одной ИСО к другой ускорение точек не меняется. Т.к. векторы сил тоже не зависят от системы отсчета, то второй закон Ньютона в них выглядит одинаково: . Выберем класс инерциальных систем отсчета. Эти системы могут двигаться с разными скоростями, но их относительные ускорения нулевые, поэтому при переходе от одной ИСО к другой ускорение точек не меняется. Т.к. векторы сил тоже не зависят от системы отсчета, то второй закон Ньютона в них выглядит одинаково: 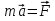 . .Эффективный диаметр молекул газа - минимальное расстояние, на которое сближаются центры двух молекул при столкновении  |

 и холодильника
и холодильника 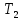 :
: