определение длины световой волны с использованием бипризмы

Название	определение длины световой волны с использованием бипризмы
Дата	12.05.2022
Размер	189.34 Kb.
Формат файла
Имя файла	Laboratornaya_rabota_2.docx
Тип	Отчет #523901

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №2

по дисциплине «Физика»

ТЕМА: «ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ИСПОЛЬЗОВАНИЕМ БИПРИЗМЫ»

Студент гр. 1370 _______________ Леонтьева Д.Е

Преподаватель __________________ Павлова Ю.В.
Санкт-Петербург

2022

Лабораторная работа 2.

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ИСПОЛЬЗОВАНИЕМ БИПРИЗМЫ

Цель работы: определение длины световой волны интерференционным методом.

Экспериментальная установка состоит из оптической скамьи с мерной линейкой; бипризмы Френеля, закреплённой в держателе; источника света со светофильтром; раздвижной щели; окуляра со шкалой. Взаимное расположе- ние элементов установки соответствует схеме, приведенной на рис. 2.1. Ис- точником света служит лампа накаливания. Светофильтр, расположенный перед лампой, пропускает определенную часть спектра излучения лампы, ко- торую и надлежит изучить.

На оптической скамье, снабженной линейкой с миллиметровой шкалой, помещены укрепленные на держателях вертикальная щель S, бипризма Р и окуляр О. Ширину щели можно изменять с помощью винта, находящегося в верхней части его оправы. Щель и бипризма могут быть повернуты вокруг горизонтальной оси, а бипризма также и вокруг вертикальной оси. Для полу- чения отчетливых интерференционных полос необходимо, чтобы плоскости щели и основания бипризмы были параллельны. Это достигается соответ- ствующим поворотом бипризмы и/или щели. Окуляр О служит для наблюде- ния интерференционной картины. Для измерения расстояния между полоса- ми он снабжен шкалой, цена малого деления которой составляет 0.1 мм.

Общие сведения

Один из способов наблюдения интерференции световых волн основан на использовании бипризмы Френеля. Бипризма Френеля представляет собой две призмы с очень малым преломляющим углом , сложенные основаниями. Схема наблюдения интерференционной картины с помощью бипризмы пока- зана на рис. 2.1. От источника света S (щели) лучи падают на обе половины бипризмы Р, преломляются в ней и за призмой распространяются так, как ес- ли бы исходили из двух мнимых источников S₁и S₂. Действительно, если смотреть через верхнюю половину бипризмы, то светящаяся щель S будет ка- заться расположенной в точке S₁, а если смотреть через нижнюю половину бипризмы, то расположенной в точке S₂. За призмой имеется область про- странства, в которой световые волны, преломлённые верхней и нижней поло- винами бипризмы, перекрываются (на рис. 2.1 эта область заштрихована).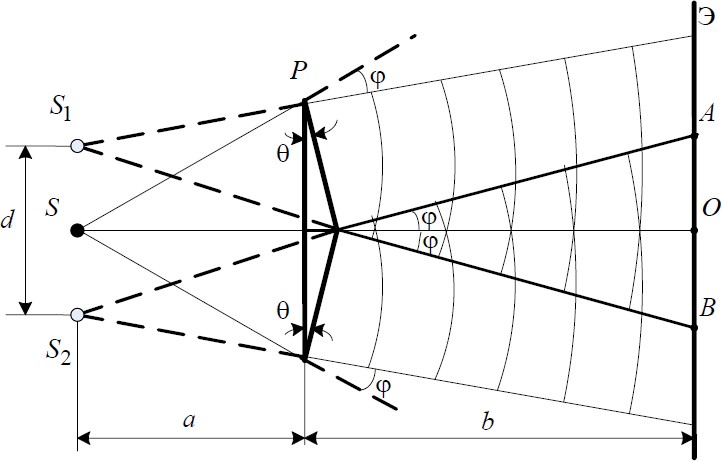

Рис. 2.1. Получение интерференционной картины с использованием бипризмы Френеля

В этой области пространства сводятся воедино две части каждогоцугаволн

от источника S, прошедшие разные оптические пути, способные при выпол-

нении условия

  l_ког ²

 интерферировать, где Δ – оптическая раз-

ность хода лучей, l_ког– длина когерентности, λ – средняя длина волны излу- чения, Δλ – интервал длин волн, представленных в данной волне. При этом колебания в точках, удалённых на расстояние большее l_когвдоль распростра- нения волны, оказываются некогерентными. Для обычных источников в оп- тике длина когерентности составляет 3–30 см.

Интерференционная картина, получающаяся при этом, соответствует интерференции волн, исходящих из двух когерентных источников, располо- женных в точках S₁и S₂, и на экране Э в области АВ наблюдается тогда ряд светлых и тёмных полос, параллельных ребру бипризмы. Светлые полосы лежат в тех местах экрана, куда приходят волны от источников S₁и S₂с раз- ностью хода, равному чётному числу длин полуволн, тёмные — в тех местах, куда приходят волны с разностью хода, равной нечётному числу полуволн. Расстояние x между светлыми (или тёмными) полосами интерференцион- ной картины составляет

^^x^^a^^b^₀

d l₀d,

(2.1)

где aи b― соответственно расстояния от щели до бипризмы и от бипризмы

до экрана;

l a b;

λ₀― длина волны излучения источника в вакууме; d―

расстояние между мнимыми источниками, равное (см. рис. 2.1)

d 2atg  2a.

Докажите, что в случае, когда преломляющий угол θ приз-

мы мал, и углы падения на грань призмы не очень велики, все лучи отклоня- ются каждой из половин бипризмы на практически одинаковый угол φ, рав-

ный

^^^ⁿ^¹

(n– показатель преломления материала призмы (стекла)).

Тогда для расстояния dполучаем

^d^²^a^ⁿ^¹^.

C учётом этого соотношения вместо выражения (2.1) имеем

^^x^^l^₀²^a^ⁿ^¹^,
(2.2)
(2.3)

или

^₀^²^a^ⁿ^¹^^x^l^.
(2.4)

Выражения (2.3) или (2.4) устанавливают связь между длиной световой волны и геометрическими размерами системы (т. е. источник света – биприз- ма Френеля – экран), в которой реализуется явление интерференции.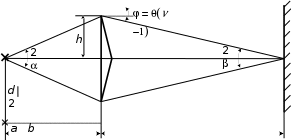

S O
S₂
Рис. 2.2. Определение апертуры и угла схождения лучей в опыте с бипризмой Френеля

Видимость интерференционной картины зависит от размеров источника света, в чём нетрудно убедиться, изменяя ширину щели. Существенным яв- ляются, однако, не сами по себе размеры щели, а угол 2 (рис. 2.2). Угол 2 между соответствующими лучами, идущими от S через каждую из двух вет- вей интерферометра к О, представляет собой угол раскрытия лучей, опреде- ляющий интерференционный эффект в точке О. Практически то же значение

имеет этот угол и для любой другой точки интерференционного поля. Этот угол называется апертурой интерференции. Ему соответствует в поле ин- терференции угол схождения лучей 2, величина которого связана с углом 2 правилами построения изображений. При неизменном расстоянии до экрана 2 тем больше, чем больше 2.

Из рис. 2.2 видно, что

2  d

^a^^b^.

(2.5)

Подставляя выражение (2.5) в (2.1), получаем для расстояния между ин- терференционными полосами

Из рис. 2.2 видно также, что

x 

²^^.

(2.6)

^^^^^^ⁿ^¹

(2.7)

и, кроме того,

ha , hb .

Исключая из двух последних выражений ве-

личину h, получаем

 ab.
(2.8)

Из совместного рассмотрения выражений (2.7) и (2.8) для углов  и 

находим

^^^ⁿ^¹^b

^^^ⁿ^¹^a

^a^^b^,

^a^^b^.

(2.9)

(2.10)

Эти соотношения используются в последующем для расчётов.

Величина апертуры интерференции 2 тесно связана с допустимыми размерами источника. Теория и опыт показывают, что с увеличением аперту- ры интерференции уменьшаются допустимые размеры ширины источника, при которых ещё имеет место отчётливая интерференционная картина. Усло- вие хорошего наблюдения интерференции от протяжённого источника ши- рины s можно записать в виде:

stg   4.

(2.11)

Это условие, несмотря на его приближенный характер, можно положить в основу расчётов допустимых размеров монохроматического источника.

В данной работе монохроматизация света осуществляется с помощью светофильтра. Нетрудно найти связь между порядком интерференции m и шириной спектрального интервала , пропускаемого светофильтром. Дей- ствительно, интерференция не будет наблюдаться, если максимум m-го по рядка для ( + ) совпадёт с максимумом (m+ 1)-го порядка для : (m+ 1)

=m( + ), т. е.  = /m. Для того, чтобы интерференционная картина при данных значениях  и  обладала высокой видимостью, приходится ограни- чиваться наблюдением интерференционных полос, порядок которых много меньше предельного m_max, определяемого условием

m_max  .

(2.12)

Экспериментально определяемая ширина полос рассчитывается по формуле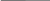

__x_(N₂ N₁)c_,

m1
(2.13)

где m― число полос, которые по яркости хорошо видны на экране,

N₁и N₂

– положения первой и последней полосы этого набора в делениях шкалы

окуляра,

с 0.1 мм дел

— масштабный множитель.

Ширина области перекрытия волн на экране (рис. 2.1) имеет протяжен-

ность

AB 2btgφ  2bφ  2b(n1)θ. Тогда максимальное число интерферен-

ционных полос, которое можно наблюдать на экране с учетом формулы (2.13) равно

_N_max_AB_2b(n1)θ _
(2.14)

x x

Подставляя выражение для xиз формулы (2.13), получим

4ab(n1)²θ²

^Nmax ^

lλ₀

 (2.15)

Протокол наблюдений

Лабораторная работа №2

ОПРЕДЕЛЕНИЕ ДЛИНЫ СВЕТОВОЙ ВОЛНЫ С ИСПОЛЬЗОВАНИЕМ БИПРИЗМЫ

Таблица2.1

Константы эксперимента n, θ , cзаносятся с панели установки. см. п.7 указаний по проведению эксперимента

c	θ	n	^Nmax
мм/дел	Рад	–	–

Таблица2.2

Выборка значений длины волны, излучаемой источником

l a bмм, ^θ_a^^θ_l^^1мм, ^θ_N^^0,1^дел, d 2θ(n1)

l ...

№	a	N₁	N₂	m	__x_(N₂ N₁)c m 1	_λ₀_2aθ(n 1)x l	_θλ __λ^θ_a_θ_l_2θ_N^ ^a l N₂ N₁^  
	мм	дел	дел	−	мм	нм	нм
1
2
3
4
5

ИДЗ
Вариант 11
№11. Какие волны называются монохроматическими?

Монохроматическая волна – это строго гармоническая (синусоидальная) волна с постоянными во времени частотой, амплитудой и начальной фазой.
№ 39. Интерференция при прохождении света через плоскопараллельную пластинку? Покажите ход лучей. Рассчитайте оптическую разность хода.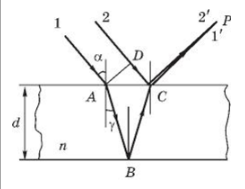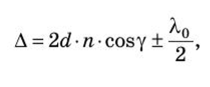

где у — угол преломления.

В случае плоскопараллельной пластинки, т.е. d = const, оптическая разность хода лучей 1 и 2, приходящих в точку С, равна (см. замечание к формуле (2.37))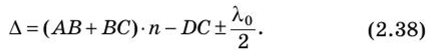

После несложных геометрических преобразований и с учетом того, что показатель преломления прозрачной пластинки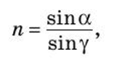

получим выражение для оптической разности хода интерферирующих лучей: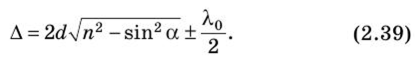