эл.геометрия. Сборник задач по применению метода геометрических преобразований к решению геометрических задач
 Скачать 15.81 Kb. Скачать 15.81 Kb.
|
|
Карпычева Полина Андреевна, МАТ-2031z Сборник задач по применению метода геометрических преобразований к решению геометрических задач Параллельный перенос С помощью циркуля и линейки постройте четырёхугольник ABCD по четырём сторонам и углу между AB и CD. Решение. Четырёхугольник ABCD построен. Обозначим угол между прямыми AB и CD через α. Проведём через вершину C прямую, параллельную AB, а через вершину A — прямую, параллельную BC. Пусть 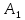 — точка пересечения проведённых прямых. Тогда — точка пересечения проведённых прямых. Тогда 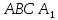 — — параллелограмм. Поэтому 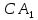 = AB. Отсюда вытекает следующий способ построения. Строим треугольник = AB. Отсюда вытекает следующий способ построения. Строим треугольник 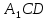 по двум сторонам и углу α между ними. Затем строим треугольник с основанием по двум сторонам и углу α между ними. Затем строим треугольник с основанием 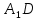 и боковыми сторонами DA и и боковыми сторонами DA и 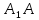 = BC. Через точки A и C проводим прямые, параллельные = BC. Через точки A и C проводим прямые, параллельные 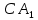 и и 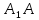 соответственно. соответственно.С помощью циркуля и линейки постройте четырёхугольник по трём сторонам и углам, прилежащим к четвёртой. Из вершины B параллелограмма ABCD проведены его высоты BK и BH. Известны отрезки KH = a и BD = b. Найдите расстояние от точки B до точки пересечения высот треугольника BKH. Осевая симметрия Вамрва Вам вам Центральная симметрия Пмапмпав Аемрив Поворот 1) 2) 3) Гипотетия |
