Мат анализ. Контрольная работа дисциплина Математический анализ Ф. И. О студента Татарчук Полина Андреевна Направлениеспециальность Экономика
 Скачать 215.97 Kb. Скачать 215.97 Kb.
|
   МИНОБРНАУКИ РОССИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Новосибирский государственный университет экономики и управления «НИНХ» (ФГБОУ ВО «НГУЭУ», НГУЭУ) Кафедра математики и естественных наук КОНТРОЛЬНАЯ РАБОТА Дисциплина: Математический анализ Ф.И.О студента: Татарчук Полина Андреевна Направление/специальность: Экономика Номер группы: Э71Д Номер варианта контрольной работы: 5 Номер зачетной книжки: 152835 Дата регистрации контрольной работы кафедрой: _______________________ Проверил: _________________________________________________________ Новосибирск 2018 Задача 1. Вычислить пределы функций а) 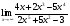 ; ;б) 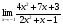 ; ;в) 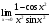 ; ;г) 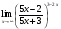 . .Решение задачи: а) 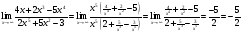 б) 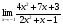 Разложим числитель и знаменатель на множители 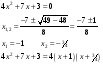 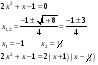 Тогда 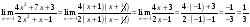 в) 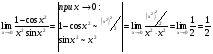 г) 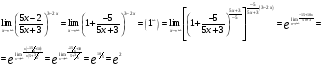 Задача 2. Найти производную функции: а) 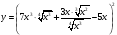 б) 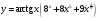 в) 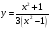 г) 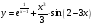 Решение задачи: а) 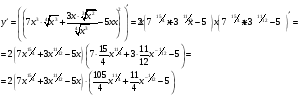 б) 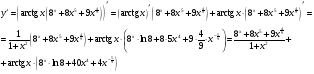 в) 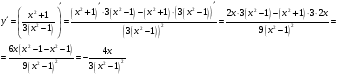 г) 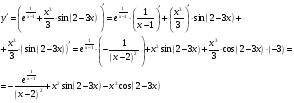 Задача 3. Провести полное исследование функции 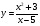 и построить ее график. и построить ее график.Решение задачи:
x-50, x5, x(-;5)(5;+)
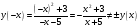 , функция свойствами четности или нечетности не обладает. , функция свойствами четности или нечетности не обладает.
Данная функция не является периодической как дробно-рациональная.
Данная функция является непрерывной на всей области определения.
а) вертикальные x=5 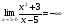 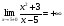 б) горизонтальные 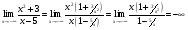 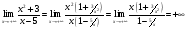 Горизонтальных асимптот нет. в) наклонные y=kx+b 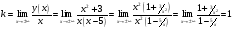 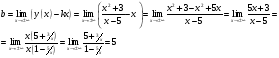 y=x+5 - наклонная асимптота
Найдем производную функции. 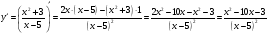 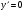 при при 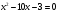 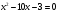 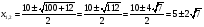 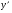 не существует при x=5 не существует при x=5Составим таблицу для определения знака первой производной:
Найдем вторую производную 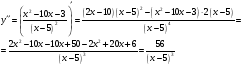 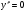 , x= , x=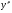 не существует при x=5 не существует при x=5Составим таблицу для определения знака второй производной
С осью OY: полагаем x=0, тогда y= 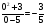 . .С осью OX: полагаем y=0, тогда 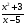 =0, x=. =0, x=.Построим график функции: 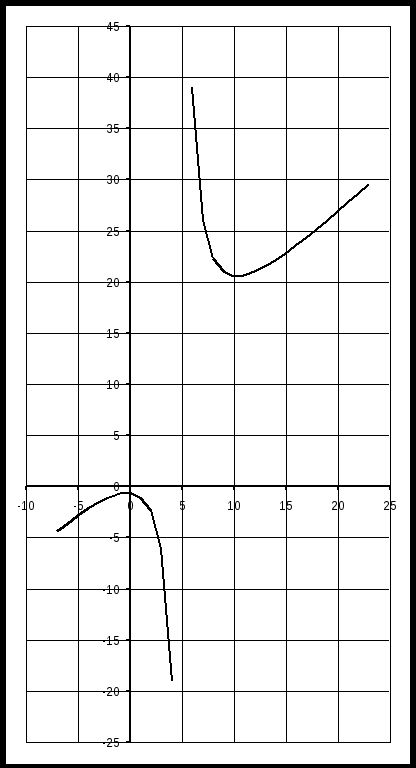 Задача 4. Исследовать на экстремум функцию двух переменных: z = -3x 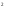 + 2xy - 4y + 2xy - 4y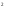 + 2x - 8y + 1 + 2x - 8y + 1Решение задачи: Областью определения данной функции является вся координатная плоскость. Найдем частные производные 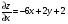 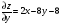 Найдем критические точки функции 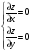 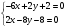 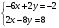 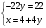 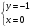 M(0;-1) M(0;-1)Получилась одна точка, подозрительная на экстремум. Найдем частные производные второго порядка 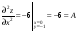 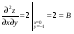 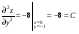 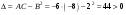 , в точке M есть экстремум. Т.к. A<0, то в точке M – максимум. Найдем значение функции в точке M: , в точке M есть экстремум. Т.к. A<0, то в точке M – максимум. Найдем значение функции в точке M:zmax=-302+ 20(-1) - 4(-1)2 + 20 - 8(-1) + 1=5 Задача 5. Проверить удовлетворяет ли функция z = z(x, y) дифференциальному уравнению: 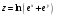 , , 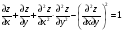 Решение задачи: 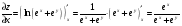 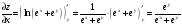 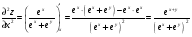 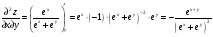 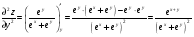 Тогда 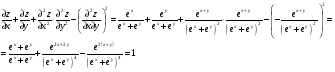 Т.к. 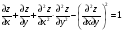 , то функция z = z(x, y) удовлетворяет данному дифференциальному уравнению. , то функция z = z(x, y) удовлетворяет данному дифференциальному уравнению.БИБЛИОГРАФИЧЕСКИЙ СПИСОК
|

 )
)