Лаба 2 ЛЭТИ физика. Лаба 2. Определение длины световой волны с использованием бипризмы
 Скачать 163.47 Kb. Скачать 163.47 Kb.
|
|
| Студент гр. 0000 | | Иванов И.И. |
| Преподаватель | | Иванов И.И. |
Санкт-Петербург
2022
Цель работы.
Определение длины световой волны интерференционным методом.
Основные теоретические положения.
Экспериментальная установка состоит из оптической скамьи с мерной линейкой; бипризмы Френеля, закреплённой в держателе; источника света со светофильтром; раздвижной щели; окуляра со шкалой. Источником света служит лампа накаливания. Светофильтр, расположенный перед лампой, пропускает определенную часть спектра излучения лампы, которую и надлежит изучить.
Бипризма Френеля представляет собой две призмы с очень малым преломляющим углом θ, сложенные основаниями.
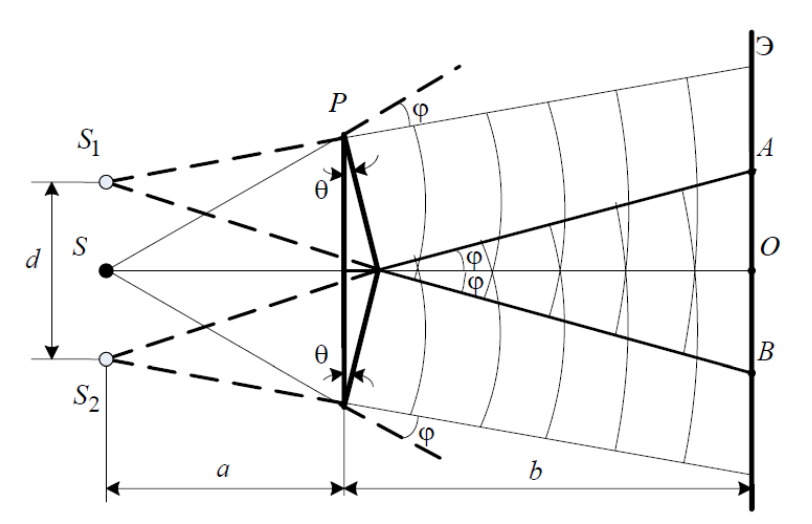
Рис. 1. Получение интерференционной картины с использованием бипризмы Френеля
От источника света S (щели) лучи падают на обе половины бипризмы Р, преломляются в ней и за призмой распространяются так, как если бы исходили из двух мнимых источников S1 и S2. За призмой имеется область пространства, в которой световые волны, преломлённые верхней и нижней половинами бипризмы, перекрываются.
В этой области пространства сводятся воедино две части каждого цуга волн от источника S, прошедшие разные оптические пути, способные при выполнении условия
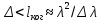 интерферировать, где Δ – оптическая разность хода лучей,
интерферировать, где Δ – оптическая разность хода лучей, 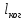 – длина когерентности, λ – средняя длина волны излучения, Δλ – интервал длин волн, представленных в данной волне.
– длина когерентности, λ – средняя длина волны излучения, Δλ – интервал длин волн, представленных в данной волне.Расстояние x между светлыми (или тёмными) полосами интерференционной картины составляет
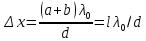 (1)
(1), где a и b ― соответственно расстояния от щели до бипризмы и от бипризмы до экрана;
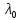 ― длина волны излучения источника в вакууме; d ― расстояние между мнимыми источниками.
― длина волны излучения источника в вакууме; d ― расстояние между мнимыми источниками.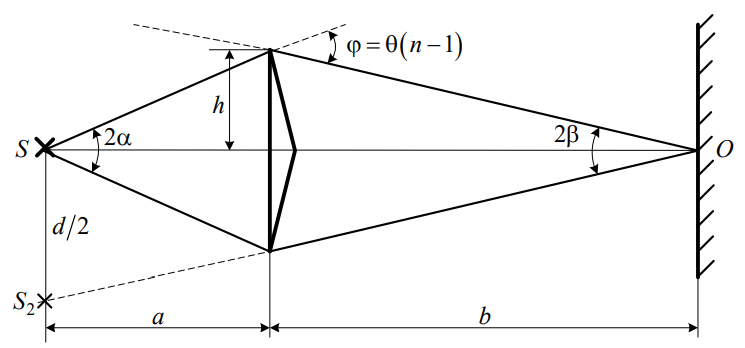
Рис. 2. Определение апертуры и угла схождения лучей в опыте с бипризмой Френеля
Для определения расстояния d между мнимыми источниками рассмотрим ход луча через одну из половин бипризмы (рисунок 2). Для точки О в соответствии с законом преломления n=sin i1/sini2 , где n – показатель преломления материала призмы (стекла); i1 и i2 – углы падения и преломления. Вследствие малости углов справедливо i1=ni2. Аналогично для точки М имеем i4=ni3. Рассматривая треугольники ОKМ и ОNM, можно показать, что справедливы соотношения i2+i3=θ и (i1-i2)+(i4-i3)=φ. Из этих соотношений для угла φ отклонения луча половиной бипризмы несложно получить φ=θ(n-1) .
Таким образом, в рамках использованных допущений все лучи отклоняются каждой из половин бипризмы на одинаковый угол. Расстояние d, как видно из рисунка 1, равно
d=2atgφ≅2aφ=2aθ(n-1) (2)
C учетом этого соотношения вместо выражения (1) имеем
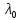 =2aθ(n-1)∆x/a+b (3)
=2aθ(n-1)∆x/a+b (3)Видимость интерференционной картины зависит от размеров источника света, в чем нетрудно убедиться, изменяя ширину щели.
Для интерференционного эффекта существенны, однако, не сами по себе размеры щели, а угол 2α между соответствующими лучами, идущими от S через каждую из двух ветвей интерферометра к точке О. Этот угол, который представляет собой угол раскрытия лучей, называется апертурой интерференции.Ему соответствует в поле интерференции угол схождения лучей 2β,величина которого связана с углом2αправилами построения изображений. При неизменном расстоянии до экрана 2β тем больше, чем больше 2α.
Из рисунка 2 видно, что
2β≅d/(a+b). (4)
Подставляя выражение (4) в (1), получаем для расстояния между интерференционными полосами
∆x=λ/2β. (5)
Из рисунка 2 видно также, что
α+β=φ=θ(n-1) (6)
и, кроме того, h/a≅α, h/b≅β .Исключая из двух последних выражений величину h, получаем
β=αa/b (7)
Из совместного рассмотрения выражений (6) и (7) находим
α=θ(n-1)b/(a+b) (8)
β=θ(n-1)a/(a+b) (9)
Величина апертуры интерференции 2α тесно связана с допустимыми размерами источника. Теория и опыт показывают, что с увеличением апертуры интерференции уменьшаются допустимые размеры ширины источника, при которых еще имеет место отчетливая интерференционная картина. Условие хорошего наблюдения интерференции от протяженного источника ширины s можно записать в виде:
stg≤λ/4 (10)
Это условие, несмотря на его приближенный характер, можно положить в основу расчетов допустимых размеров источника.
В данной работе монохроматизация света осуществляется с помощью светофильтра. Нетрудно найти связь между порядком интерференции m и шириной спектрального интервала Δλ, пропускаемого светофильтром. Действительно, интерференция не будет наблюдаться, если максимум m-го порядка для λ + Δλ совпадет с максимумом (m+1)-го порядка для λ: (m+1)λ=m (λ+Δλ),т.е.Δλ=λ/m . Для того чтобы интерференционная картина приданных значениях Δλ и λ обладала высокой видимостью, приходится ограничиваться наблюдением интерференционных полос, порядок которых много меньше предельного mmax , определяемого условием
mmaxλ/Δλ. (11)
Экспериментальные результаты.
Таблица 1
Константы эксперимента n, θ, c заносятся с панели установки.
| с | θ | n | 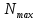 |
| мм/дел | Рад | - | - |
| 0,1 | 0,0061 | 1,52 | |
Таблица 2
Выборка значений длины волны, излучаемой источником
l = a+bмм,
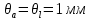 ,
,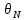 = 0,1 дел, d = 2
= 0,1 дел, d = 2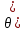 n-1) = 0,006344 рад
n-1) = 0,006344 рад| № | 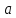 | 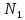 | 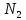 | 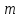 | Δx = 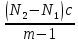 | 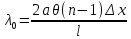 | 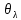 =λ =λ 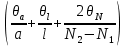 |
| | мм | дел | дел | - | мм | нм | нм |
| 1 | 200 | 7,9 | 8,5 | 5 | 0,015 | 380 | 20,247 |
| 2 | 230 | 8,2 | 8,8 | 5 | 0,015 | 430 | 19,920 |
| 3 | 250 | 8,3 | 8,9 | 5 | 0,015 | 470 | 19,745 |
| 4 | 300 | 8,3 | 8,6 | 6 | 0,006 | 570 | 36,144 |
| 5 | 350 | 8,5 | 8,9 | 5 | 0,010 | 660 | 27,538 |
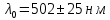
Вычисление апертуры интерференции α и угла схождения лучей β для опыта 1:
2α = 0,0038 рад
2β = 0,0024 рад
Оценка допустимого размера источника для данной апертуры α, используя неравенство stgα≤
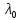 /4, отображающие условие пространственной когерентности источника света:
/4, отображающие условие пространственной когерентности источника света:s ≤
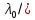 4 /tgα
4 /tgαs ≤ 0,087 мм
Оценка полосы пропускания Δλ светофильтра, используемого в данной работе:
mmax
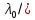 Δ
Δ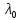 =20,08
=20,08Выводы.
Найдена длина волны
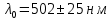 , которая входит в спектр
, которая входит в спектрзеленого света, так как источник света в опыте был зеленого света, то можно говорить о справедливости опыта. Вычислена апертура интерференции 2α = 0,0038 рад и угол схождения лучей 2β = 0,0024 рад. Оценен допустимый размер источника для данной апературы s ≤ 0,087 мм и полосы пропускаяния Δλ светофильтра, используемого в данной работе mmax 20,08.
