2 лаба. Определение световой длины световой волны с использованием бипризмы
 Скачать 219.75 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В. И. УЛЬЯНОВА (ЛЕНИНА) Кафедра физики ОТЧЁТ по лабораторной работе № 2 по дисциплине «Физика» Тема: «Определение световой длины световой волны с использованием бипризмы» Студент гр. 0232 __________________________ _______________ Преподаватель ___________________________ _______________ Санкт-Петербург 2022 г. Цель работы: определение длины световой волны интерференционным методом. Общие сведения Один из способов наблюдения интерференции световых волн основан на использовании бипризмы Френеля. Бипризма Френеля представляет собой две призмы с очень малым преломляющим углом , сложенные основаниями. Схема наблюдения интерференционной картины с помощью бипризмы показана на рис. 2.1. От источника света S (щели) лучи падают на обе половины бипризмы Р, преломляются в ней и за призмой распространяются так, как если бы исходили из двух мнимых источников S1 и S2. Действительно, если смотреть через верхнюю половину бипризмы, то светящаяся щель S будет казаться расположенной в точке S1, а если смотреть через нижнюю половину бипризмы, то расположенной в точке S2. За призмой имеется область пространства, в которой световые волны, преломлённые верхней и нижней половинами бипризмы, перекрываются (на рис. 2.1 эта область заштрихована). 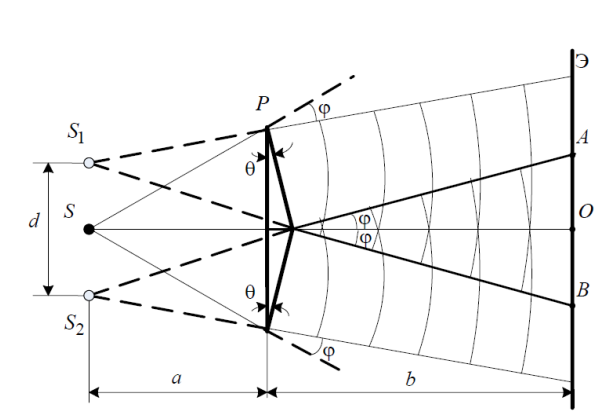 Рис. 2.1. Получение интерференционной картины с использованием бипризмы Френеля В  этой области пространства сводятся воедино две части каждого цуга волн от источника S, прошедшие разные оптические пути, способные при выполнении условия интерферировать, где Δ – оптическая разность хода лучей, lког – длина когерентности, λ – средняя длина волны излучения, Δλ – интервал длин волн, представленных в данной волне. При этом колебания в точках, удалённых на расстояние большее lког вдоль распространения волны, оказываются некогерентными. Для обычных источников в оптике длина когерентности составляет 3–30 см.И  нтерференционная картина, получающаяся при этом, соответствует интерференции волн, исходящих из двух когерентных источников, расположенных в точках S1 и S2, и на экране Э в области АВ наблюдается тогда ряд светлых и тёмных полос, параллельных ребру бипризмы. Светлые полосы лежат в тех местах экрана, куда приходят волны от источников S1 и S2 с разностью хода, равному чётному числу длин полуволн, тёмные — в тех местах, куда приходят волны с разностью хода, равной нечётному числу полуволн. Расстояние x между светлыми (или тёмными) полосами интерференционной картины составляет (2.1)  Где a и b ― соответственно расстояния от щели до бипризмы и от бипризмы до экрана; - длина волны излучения источника в вакууме; d- расстояние между мнимыми источниками, равное (см. рис. 2.1) Докажите, что в случае, когда преломляющий угол θ призмы мал, и углы падения на грань призмы не очень велики, все лучи отклоняются каждой из половин бипризмы на практически одинаковый угол φ, равный = − (n 1) (n – показатель преломления материала призмы (стекла)).Т  огда для расстояния d получаем (2.2)C  учётом этого соотношения вместо выражения (2.1) имеем(2.3) И  лиВыражения (2.3) или (2.4) устанавливают связь между длиной световой волны и геометрическими размерами системы (т. е. источник света – бипризма Френеля – экран), в которой реализуется явление интерференции. 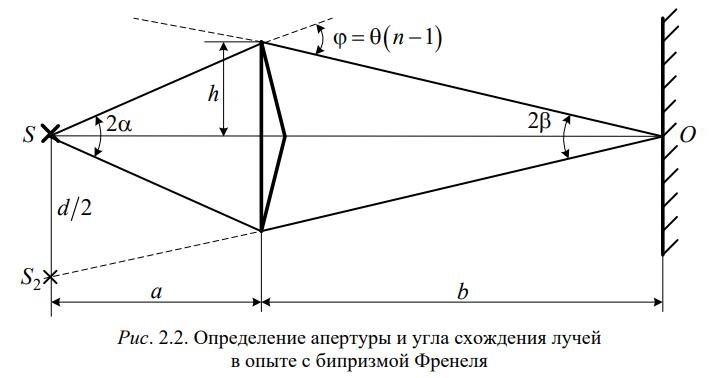 Видимость интерференционной картины зависит от размеров источника света, в чём нетрудно убедиться, изменяя ширину щели. Существенным являются, однако, не сами по себе размеры щели, а угол 2 (рис. 2.2). Угол 2 между соответствующими лучами, идущими от S через каждую из двух ветвей интерферометра к О, представляет собой угол раскрытия лучей, определяющий интерференционный эффект в точке О. Практически то же значение имеет этот угол и для любой другой точки интерференционного поля. Этот угол называется апертурой интерференции. Ему соответствует в поле интерференции угол схождения лучей 2, величина которого связана с углом 2 правилами построения изображений. При неизменном расстоянии до экрана 2 тем больше, чем больше 2. И  з рис. 2.2 видно, что (2.5)П  одставляя выражение (2.5) в (2.1), получаем для расстояния между интерференционными полосами (2.6)И  з рис. 2.2 видно также, что (2.7)и  , кроме того, h/a , h/b . Исключая из двух последних выражений величину h, получаем (2.8)И  з совместного рассмотрения выражений (2.7) и (2.8) для углов и находимЭ  ти соотношения используются в последующем для расчётов. Величина апертуры интерференции 2 тесно связана с допустимыми размерами источника. Теория и опыт показывают, что с увеличением апертуры интерференции уменьшаются допустимые размеры ширины источника, при которых ещё имеет место отчётливая интерференционная картина. Условие хорошего наблюдения интерференции от протяжённого источника ширины s можно записать в виде: (2.11)Это условие, несмотря на его приближенный характер, можно положить в основу расчётов допустимых размеров монохроматического источника. В данной работе монохроматизация света осуществляется с помощью светофильтра. Нетрудно найти связь между порядком интерференции m и шириной спектрального интервала , пропускаемого светофильтром. Действительно, интерференция не будет наблюдаться, если максимум m-го порядка для ( + ) совпадёт с максимумом (  m + 1)-го порядка для : (m + 1), =m( + ), т. е. = /m. Для того, чтобы интерференционная картина при данных значениях и обладала высокой видимостью, приходится ограничиваться наблюдением интерференционных полос, порядок которых много меньше предельного mmax, определяемого условием (2.12)Э  кспериментально определяемая ширина полос рассчитывается по формуле где m ― число полос, которые по яркости хорошо видны на экране, N1 и N2 – положения первой и последней полосы этого набора в делениях шкалы окуляра, c=0.1 мм/дел ― масштабный множитель. Ш 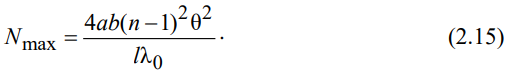  ирина области перекрытия волн на экране (рис. 2.1) имеет протяженность Тогда максимальное число интерференционных полос, которое можно наблюдать на экране с учетом формулы (2.13) равноП  одставляя выражение для x из формулы (2.13), получим |