Определение длины звуковой волны и скорости звука в воздухе методом резонанса
 Скачать 1.85 Mb. Скачать 1.85 Mb.
|
|
1 Лабораторная работаОпределение длины звуковой волны и скорости звука в воздухе методом резонанса. Оборудование: звуковой генератор с телефоном, стеклянная трубка с подвижным поршнем, измерительная линейка. Описание целей работы.
 - Рассчитывать погрешность измерений. 2  Основы теорииМеханические колебания Механические колебания – это движения, которые точно или приблизитель- но повторяются через определенные интервалы времени. Колебания могут быть свободными и вынужденными. Свободные колебания – колебания, возникающие в системе под действием внутренних сил после того, как система была выведена из положения равновесия. Примеры: колебания груза на пружине или груза, подвешенного на нити. Вынуж- денные колебания – колебания, совершаемые телами под действием каких-то внешних сил. Примеры: поплавок на воде, игла швейной машины, поршни в меха- низмах. Если колебания повторяются через точные промежутки времени, то такие колебания называются периодическими, а промежуток времени периодом Т (с). Период Т колебания – минимальный промежуток времени, через который движение тела полностью повторяется. Зная период можно определить частоту ко- лебаний. Частотой колебаний называется величина 1 , равная числу колебаний, T совершающихся за единицу времени. Частота измеряется в герцах ( Гц ): 1 Гц = 1 с –1. Отклонение точки от положения равновесия называют смещением, а наи- большее отклонение – амплитудой А. Для описания колебательного движения нужно подобрать функцию перио- дическую и непрерывную. Такими функциями являются функции cos или sin , где = (t) . Наиболее простая зависимость координаты тела от времени при ко- лебательном движении будет иметь вид: x ( t ) = А cos ( t ) или x ( t ) = A sin ( t ) (1) Уравнение (1) справедливо, если ось координат ввести вдоль движения ко- леблющейся точки, а за ее начало взять положение равновесия   Рис.1. Рис.1.Амплитуда А = | X max |, а смещение = | X | Аргумент ( t ) в уравнении (1) называют фазой колебаний. Вид функции (t) : ( t ) = t + 0 (2), где величину 2 T называют круговой (циклической) частотой, 0 – начальной фазой. 3 Положение точки при колебательном движении определяется ее фазой: : t 2 t T , где выражение t показывает, какая доля колебания прошла от начала T движения точки, а произведение мере). 2 tT переводит эту долю в угол (в радианной Если реальное колебание совершается в согласии с уравнением (1), то его называют гармоническим. Таким колебанием можно считать колебания матема- тического маятник при малых углах отклонения. Большинство колебаний в приро- де являются негармоническими, но их можно рассматривать как сумму гармониче- ских колебаний. Механические волны.Волной называют колебания, распространяющиеся в пространстве с течени- ем времени. Любое реальное тело (твердое, жидкое, газообразное) являет собой множе- ство частиц (молекул , атомов), упруго взаимодействующих между собой. Если любую точку среды вывести из положения равновесия, то она неизбежно вызыва- ет изменение положения окружающих частиц. Если создать колебание одной час- тицы, то в упругой среде колебательные движения передаются от точки к точке. Существует два типа волн: продольные и поперечные. Волны, у которых частицы среды колеблются в направлении распространения волны, называются продольными волнами. У этих волн чередуются области сгущения и разрежения (рис.2а). Волны, у которой частицы среды колеблются в плоскостях, перпендику- лярных направлению распространения волны, называются поперечными волна- ми. У этих волн происходит чередование горбов и впадин (рис.2б). 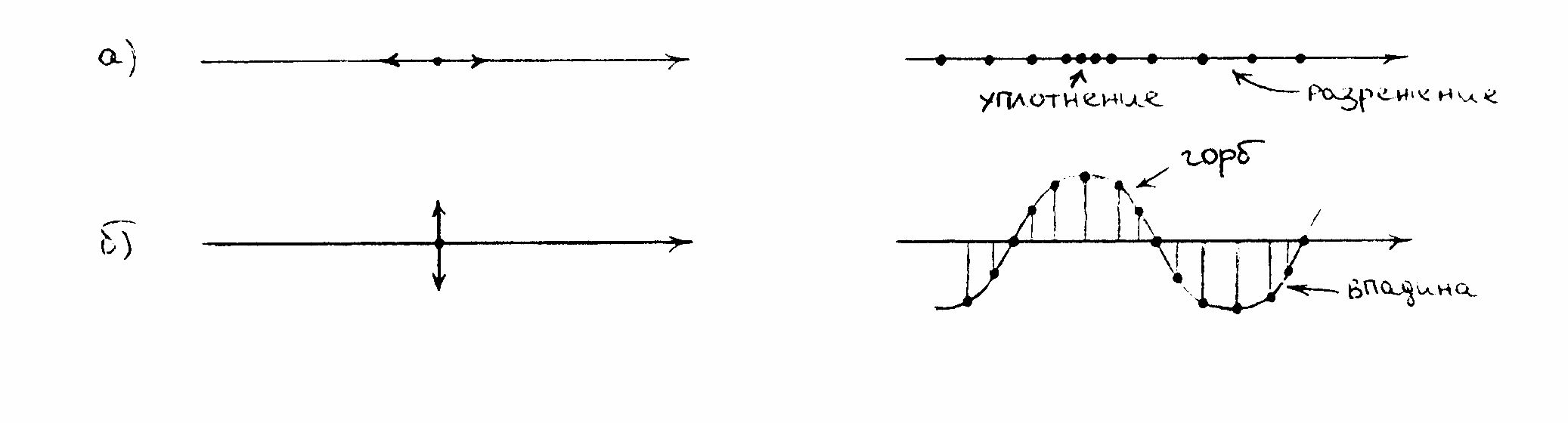 Рис 2. Продольная и поперечная волна. Таким образом, все точки среды совершают колебания около своих положе- ний равновесия не уходя при этом от своих мест. В простейшем случае все коле- бания можно считать гармоническими, происходящими с одним и тем же перио- дом (частотой), но с различной фазой. Различие фаз связано с тем, что каждая час- тица среды начинает свое колебание только после того, как вступит в движение 4 предыдущая, то есть каждая последующая точка отстает по фазе от предыдущей. Пусть на рис.3 точками условно изображены частицы линейной упругой среды. Если, например, колебательное движение сообщить первой частице, то ее уравне- ние движения будет иметь вид ( 0 = 0 ): x = A sin t. 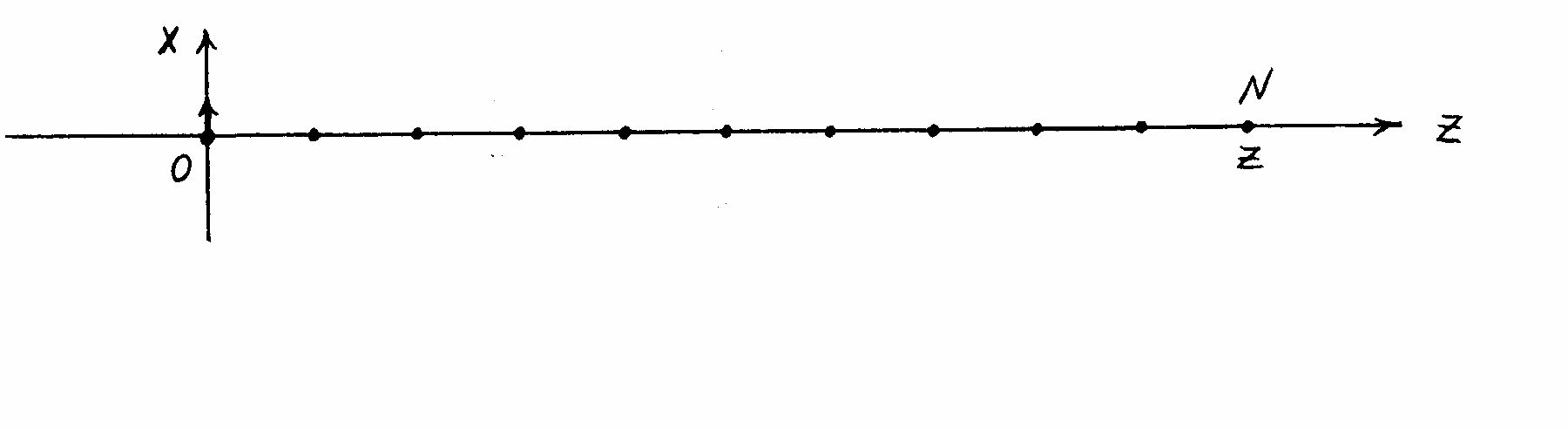 Рис.3. Распространение колебания в упругой среде. Точка N, отстоящая от первой на расстояние z вдоль направления распро- странения волны, начинает свое движение позже первой точки на промежуток времени z, где - скорость, с которой передается (распространяется) колеба- ние. Тогда уравнение ее движения будет иметь вид: x= A sin ( t - ) = A sin ( t - z) (3). Полученное выражение представляет собой уравнение плоской волны, рас- пространяющейся вдоль направления z. Расстояние, на которое распространяется колебание за один период, называ- ется длиной волны. Оно будет также равно расстоянию между ближайшими час- тицами, колеблющимися в одинаковой фазе = Т (4), где - длина волны, - скорость распространения волны, Т – период колебания. Или, учитывая, что Т = 1 / , где - частота колебаний, = (5) Интерференция волн.Если в одной и той же среде одновременно распространяются колебания от двух (и более) источников (наложение волн): то каждая волна распространяется независимо друг от друга. Тогда каждая точка (частица) среды должна будет одно- временно совершать два (или более) колебаний, то есть в каждой точке происхо- дит сложение колебаний. Так как складываемые колебания, происходящие от разных источников волн, могут иметь различные периоды и амплитуды, то результирующее колебание обычно является негармоническим. Интерес представляет случай наложения так называемых когерентных волн. Когерентными называются волны, разность фаз которых в каждой точке волнового поля постоянна. Такие волны должны не только иметь одинаковую дли- 5 ну волны и частоту, но и излучаться источниками, работающими непрерывно в течение всего времени наблюдения. При наложении когерентных волн, в каждой точке поля результирующее колебание будет тоже гармоническим с постоянной амплитудой, причем распре- деление амплитуд в волновом поле будет постоянным. Если две когерентные волны, бегущие в противоположные стороны, встре- чаются, то при их сложении образуется стоячая волна. Чаще всего, стоячие волны возникают при сложении падающей одномерной волны с волной, испытавшей от- ражение. При интерференции прямой и отраженной волн возникают участки, где ко- лебательное движение отсутствует (узлы) и участки, где колебания могут происхо- дить с наибольшей амплитудой (пучности). 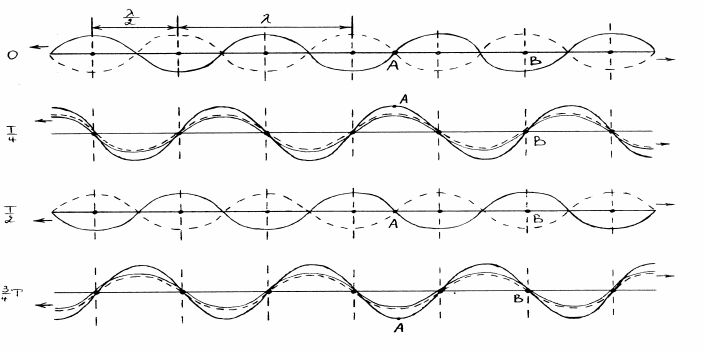 Рис.4. Образование стоячей волны. На рис.4 пунктирной и сплошной линиями изображены положения двух волн, бегущих навстречу друг другу, через промежутки времени, равные четверти периода. Стрелками указаны направления распространения обеих волн. За четверть периода каждая из волн перемещается на 1/4. Результирую- щие колебания в каждой точке возникают вследствие сложения двух колебаний. Рассмотрим движение точки А. На рис.4 при t = 0 обе волны создают в точ- ке А смещение равное нулю. Точка А остается в положении равновесия. Через   6время t = Т / 4 обе волны создают в точке А смещения, направленные в одну сто- рону, значит смещение точки А от положения равновесия удвоится. При t=3/4T обе волны опять смещают точку А в одном и том же направлении и общее смеще- ние точки удвоится. Таким образом за полный период точка А совершила колеба- ние с удвоенной амплитудой. Рассмотрим движение точки В. При t = 0, колебания создаваемые прямой и отраженной волной в этой точке создают смещения, направленные в противопо- ложные стороны. Так как их амплитуды равны, итоговое результирующее смеще- ние равно нулю и она остается в положении равновесия. При t=4/T и 3/4T обе волны оставляют точку в положении равновесия . При t=T/2 обе волны смещают точку В в противоположных направлениях и, в результате, она вновь остается в положении равновесия. Таким образом за полный период колебания точка В остается в положении равновесия. Точки, аналогичные точке В с амплитудой колебания равной нулю, будут располагаться на луче через расстояние равное /2. Такие точки называются узлами. Точки, находящиеся между узлами (аналогичные точке А), будут совер- шать результирующее колебание с удвоенной амплитудой (см.рис.4). Такие точки называются пучностями. Они так же будут повторяться через /2. Расстояние ме- жду узлом и пучностью равно /4. На рис.4 видно, что узлы и пучности не перемещаются вдоль луча. Это про- исходит потому, что разность фаз двух колебаний в пучностях и узлах (как и во всех других точках) не меняется со временем. Она зависит только от положения точки на луче. В результате распределение смещений точек относительно их по- ложений равновесия в любой момент времени образует волну, которая не переме- щается в пространстве. Такая волна называется стоячей волной. Расстояние между соседними узлами (или пучностями), как хорошо видно на рис.4, равно половине длины волны.
Звуковыми (или акустическими) волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах от 20 Гц до 20 кГц. Вол- ны указанных частот, воздействуя на слуховой аппарат человека, вызывают ощу- щение звука. Волны с 16 Гц (инфразвуковые) и 20 кГц (ультразвуковые) органами слуха человека не воспринимаются.  Описание экспериментальной установки. Описание экспериментальной установки.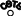  7   Рис. 5. Экспериментальная установка. На звуковых волнах легко могут быть обнаружены характерные явления интерференции. Простейший опыт по интерференции звука осуществляется с по- мощью экспериментальной установки, состоящей из следующих частей (см.рис.5): Звуковой генератор 3Г. Телефон Т. Стеклянная трубка О с подвижным поршнем П. Измерительная линейка Л. В стеклянной трубке звуковые волны, создаваемые телефоном, распростра- няются вдоль трубки и отражаются от поршня. Если расстояние от телефона до поршня кратно /2, то в трубке возникает стоячая звуковая волна. Причем у от- крытого конца трубки будет пучность волны и наблюдается резкое усиление звука, а у поршня всегда будет узел. Если, двигая поршень, менять длину трубки, то мы будем наблюдать перио- дическое усиление и ослабление звука (такое явление называют акустическим ре- зонансом). Расстояние, на которое смещается поршень между двумя последова- тельными усилениями или ослаблениями звука, будет равно /2. Звуковой генератор (3Г).Этот прибор может издавать электромагнитные колебания частотой от 20 до 20000 Гц., т.е. звуковой частоты. Если на выходе генератора укрепить телефон, то телефон преобразует электромагнитные колебания в механические той же час- тоты (т.е. “ превращает ” в звук). Получаемую частоту можно менять с помощью диска, укрепленного на передней панели генератора. На лицевую панель генератора (рис.6) выведены тумблер включения генера- тора в сеть; сигнальная лампочка Ф; переключатель поддиапазонов ПД на три фик- сированных положения, отмеченных “х1”, “х10”, ”х100”; диск РШ с неравномер- ной шкалой деления (от 20 до 200) ; указатель шкалы У; ручка переменного рези- стора, позволяющая менять амплитуду выходного сигнала; выходные зажимы, рассчитанные на подключение цепей с разным сопротивлением (5, 600, 5000 Ом); также закреплены скобы Ск для предохранения органов управления от поврежде- 8 ния. Прибор закрыт металлическим кожухом К, на котором смонтирована ручка Р для переноски прибора. С тыльной стороны имеется панель для предохранителей и сетевого шнура. Перед началом работы: Ручку “Усиление” устанавливают в крайнее левое положение поворотом против часовой стрелки; Телефон подключают к зажимам “Общ.” и ”600 Ом”, т.е. выбирают такие выходные зажимы генератора, чтобы сопротивление между ними было близким к сопротивлению подключаемого телефона; Устанавливают нужную частоту. Если для опытов необходимы частоты 20- 200 Гц., то переключатель ПД устанавливают в положение “х1”, если 200-2000 Гц – в положение “х10”, а для частот 2000-20000 Гц. используют положение “х100”. Плавную регулировку частоты осуществляют поворотом диска РШ. - Включение прибора в сеть осуществляют установкой тумблера в положе- ние “Вкл.”. - Амплитуду выходного сигнала увеличивают до необходимого значения поворо- том ручки “Усиление” по часовой стрелке. Рис. 6. Звуковой генератор. 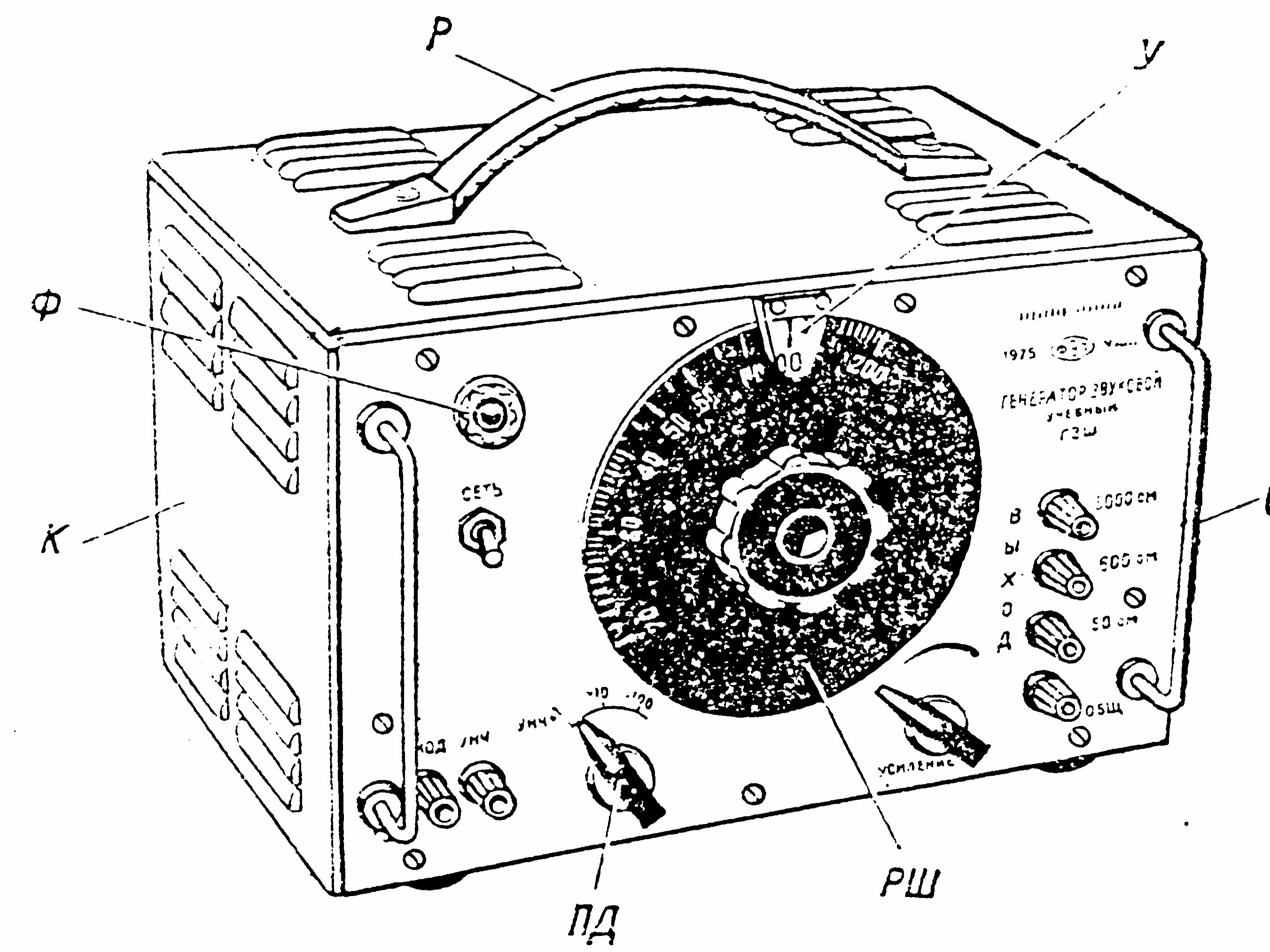 2.2. Порядок выполнения работыПеред тем, как приступить к работе, необходимо ознакомиться с эксперимен- тальной установкой и получить разрешение преподавателя на выполнение работы. Включите генератор в сеть и переключите тумблер “сеть” на панели 3Г в поло- жение “Вкл.” (при этом загорится сигнальная лампочка). Спустя 2-3 мин., переключая соответствующий диапазон и вращая диск, устано- вите указатель частоты на цифру, указанную преподавателем. Запишите эту часто- ту в таблицу. 9 Целесообразно сразу подсчитать погрешность определения частоты . Если вы точно совместили деления по шкале, то погрешность прибора по частоте не пре- вышает = ( 0,1 + 1 ) Гц. Например, при = 2600 Гц, = ( 0,1 х 2600 + 1 ) = 261 Гц. Запишите полученную погрешность в таблицу. Установите в стеклянной трубке поршень рядом с телефоном. Вращая ручку регулятора “Усиление”, установите силу звука такой , чтобы сиг- нал был едва слышен. Медленно и равномерно отодвигайте поршень от телефона до тех пор, пока не произойдет резкое усиление звука. При этом необходимо отметить мелом на стек- лянной трубке положение поршня. Двигая поршень дальше, произойдет еще одно усиление звука и мы отмечаем следующее положение поршня. Проводя измерения по всей длине стеклянной трубки, мы получим ряд точек, соответствующих пучно- стям звуковой волны. Чтобы узнать среднее расстояние lмежду ближайшими точками, необходимо измерить линейкой расстояние S между крайними точками и разделить его на 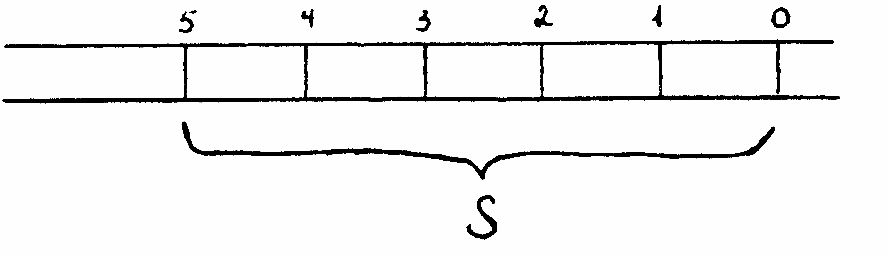 число отрезков соединяющих эти точки. Например, на рис.7 значение lзапишите в таблицу. число отрезков соединяющих эти точки. Например, на рис.7 значение lзапишите в таблицу.l S. Полученное 5 Рис.7 Нахождение среднего расстояния. Стерев мел, но не меняя частоты, проведем измерения (п.п.6,7) повторно. За- пишем вновь полученное значение l. Повторив измерения несколько раз (от 3 до 8 раз) запишем все значения lв табли- цу. Например: при =2600 Гц, l=6,2 см; 6,5 см; 6,6 см; 6,7 см ; 6,4 см ; 7,1 см ; 6,3 см. По полученным значениям li, мы находим среднее значение l : = l = 1 n (6) n l ср li i1 В нашем примере: l = 6,2 6,5 6,6 6,7 6,4 7,1 6,3 6,54 см. 7 Значение l запишите в таблицу. По формуле 2l (7), где l l вычислить длину звуковой волны и результат записываем в таблицу. В нашем примере : = 2 6,54 см = 13,08 см = 1308 10-4 м. Вычислим погрешность длины волны: 2l. Измерение l - прямое измере- ние, поэтому за истинное значение lберется её среднее значение по нескольким измерениям. Погрешность мерениям, то есть : lрассчитаем как среднюю погрешность по всем из- l = < В нашем примере: li > = 1 n n i1 li , где li 10 = < l> - li l1 = 6,54 - 6,2 = 0,34 см l2 = 6,54 - 6,5 = 0,04 см l3 = 6,54 - 6,6 = - 0,06 см l4 = 6,54 - 6,7 = - 0,16 см l5 = 6,54 - 6,4 = 0,14 см l6 = 6,54 - 7,1 = - 0,56 см l7 = 6,54 - 6,3 = 0,24 см = < > = 1 n = 0,34 0,04 0,06 0,16 0,14 0,56 0,24 см l li i1 li 0,22 7 n тогда 2l 20,22 см = 0,44 см. Найденное значение запишем в таблицу. Вычислим скорость распространения звука по формуле её в таблицу. (5) и запишем Например = 130810-4 м 2600 Гц 340 м. с Погрешность определения скорости звука находится как погрешность косвен- ного измерения, по формуле: (8). И значение записывается в таблицу. Например : =340 м( 261Гц 0,44см) 46 м. с 2600Гц 13,08см с Поменяем частоту и повторим измерения (см. п.п. 3,6-13) , Не забывая записывать результаты в таблицу. После окончания работы выключите звуковой генератор. Запишите ответы в виде : , где 1 2 3 3 1 2 3 3 Таблица
Литература Майсова Н.Н. Практикум по общему курсу физики. Савельев И.К. Курс общей физики. Евграфова Н.Н. Курс физики Сивухин Д.В. Общий курс физики. 11 Яворский Б.М., Детлаф А, Физика |
