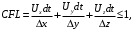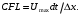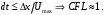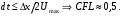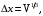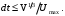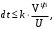Эффективный шаг интегрирования для DES метода. 1-Прокопец. Определение эффективного шага интегрирования при моделировании внешнего обтекания с помощью des метода
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Определение эффективного шага интегрирования при моделировании внешнего обтекания с помощью DES метода Прокопец С.С., Терехин А.А., Кичатов В.В., Мартынов С.И. Южно-Уральский государственный университет, Челябинск В статье приводится алгоритм определения оптимального шага интегрирования по времени на примере численного моделирования внешнего обтекания куба при использовании DES метода (метода отсоединенных вихрей). Ключевые слова: шаг интегрирования, DES, метод отсоединенных вихрей, математическое моделирование, вычислительная гидрогазодинамика, число Куранта. Численное моделирование внешнего обтекания летательных аппаратов (ЛА) на закритических углах атаки с использованием уравнений Навье-Стокса осредненных по Рейнольдсу, замкнутых полуэмпирической моделью турбулентности (RANS) [1], приводит к существенным погрешностям при определении аэродинамических характеристик (АДХ) ЛА [2]. В области закритических углов атаки рекомендуется использовать более сложные подходы моделирования внешнего обтекания, такие как LES (Large Eddy Simulation) и DES (Detached Eddy Simulation) методы [3]. Если сравнивать вычислительные затраты на постановку численного эксперимента, то метод DES является более предпочтительным по отношению к LES методу [4]. При использовании LES и DES необходимо решать нестационарную задачу, для определения параметров потока, изменяющихся по времени. Следовательно, возникает задача определение эффективного шага интегрирования для временного отрезка моделирования процесса. Устойчивость решения численного моделирования для нестационарной постановки задачи можно оценить с помощью критерия Куранта ( 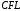 ) [5]. ) [5].Для оценки шага интегрирования по времени рекомендуется использовать следующие условие [5]:
где 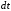 – шаг по времени; – шаг по времени;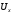 , ,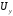 , ,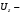 компоненты вектора скорости; компоненты вектора скорости;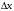 , ,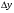 , ,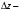 характерный размер граней элемента, в направлении советующих векторов скорости. характерный размер граней элемента, в направлении советующих векторов скорости.Рассмотрим прямоугольную ячейку (рисунок 1) с наибольшей длиной ребра 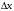 , через которую проходит поток со скоростью , через которую проходит поток со скоростью 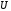 , движущийся слева направо. Для прохождения потока через ячейку, требуется временной интервал времени , движущийся слева направо. Для прохождения потока через ячейку, требуется временной интервал времени 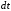 . .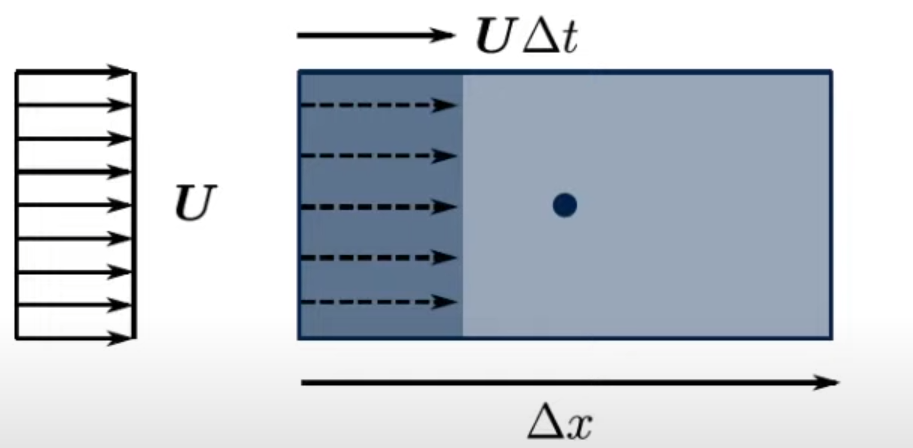 Рисунок 1 – Перемещение потока по ячейки за единицу времени В таком случае, числом Куранта ( 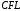 ) является отношение расстояния, пройденного потоком, движущегося в поперечном направлении, за единицу времени к длине ячейки [6]: ) является отношение расстояния, пройденного потоком, движущегося в поперечном направлении, за единицу времени к длине ячейки [6]:
Временной шаг должен быть достаточно малым, чтобы обеспечить необходимое временное разрешение потока при его прохождении через ячейку [1,7]:
Для учета различий между мгновенными и усредненными скоростями, шаг интегрирования ( 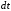 ) может быть оценен по следующей зависимости [6]: ) может быть оценен по следующей зависимости [6]:
Для любых задач, кроме акустических, рекомендуется иметь максимальное локальное число Куранта 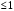 в областях, представляющих наибольший интерес [7]. в областях, представляющих наибольший интерес [7]. Интересующей областью в методе DES является область фокуса – область моделирования крупных вихрей [8]. В данной области ячейки должны быть изотропны, т.е. иметь одинаковые размеры по трем направлениям, тогда [4,8]:
где 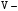 объем ячейки. объем ячейки.Сеточная модель представляет собой структурированную гекса-сетку на основе блочной топологии, построенную в сеточном генераторе ANSYS ICEM CFD [9]. В таком случае шаг интегрирования по времени оценим следующим образом [6,8]:
Для получения результатов по формуле (6), настроим пользовательскую функцию временного шага в ANSYS-CFX-Post. После постобработки результатов, минимальный временной шаг равен  Стоит обратить внимание на то, что значение Стоит обратить внимание на то, что значение 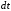 может быть выбрано большее, если минимальный масштаб времени обнаруживается вдали от области фокуса, а так же, если область с наименьшими временными масштабами не оказывают влияния на остальную область. может быть выбрано большее, если минимальный масштаб времени обнаруживается вдали от области фокуса, а так же, если область с наименьшими временными масштабами не оказывают влияния на остальную область. Оценим число Куранта при 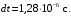 Как видно по рисунку 2, число Куранта не превышает 1, следовательно, данный временной шаг можно использовать при настройках нестационарного решения задачи с использованием DES метода. Как видно по рисунку 2, число Куранта не превышает 1, следовательно, данный временной шаг можно использовать при настройках нестационарного решения задачи с использованием DES метода. 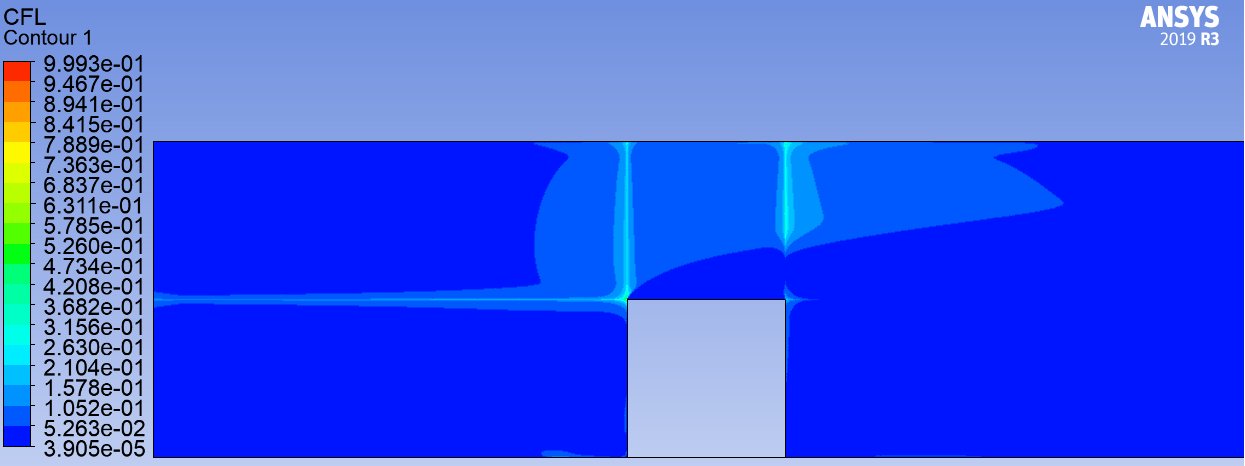 Рисунок 2 – Число Куранта при  Однако, при таком достаточно маленьком 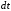 , расчет требует больших вычислительных ресурсов. При полном времени моделировании процесса 0,08 с., расчет составляет 62500 итераций, уровень невязок [10] в решении , расчет требует больших вычислительных ресурсов. При полном времени моделировании процесса 0,08 с., расчет составляет 62500 итераций, уровень невязок [10] в решении 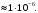 Время расчета можно сократить, подобрав оптимальный шаг интегрирования, при этом сохраняя приемлемый для расчетов уровень невязок ниже 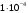 [1]. [1].Методом последовательных приближений [11] подобран оптимальный шаг интегрирования 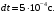 Уровень невязок не превышает необходимого значения Уровень невязок не превышает необходимого значения 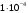 . . 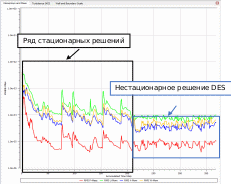 Рисунок 3 – Результаты решения предварительного стационарного решения и нестационарного решения методом DES. Расчет (рисунок 3) составляет 160 итераций, на каждом шаге по времени проводится от 4 до 6 внутренних итераций решателя, что обеспечивает сходимость невязок основных физических величин до 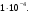 Среднее значение числа Куранта в интересующей области Среднее значение числа Куранта в интересующей области 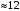 . Следовательно, решение можно считать приемлемым для последующего инженерного анализа полученных данных. Физическое время решения составляет 20 часов, объем занимаемой памяти 550 Гб. . Следовательно, решение можно считать приемлемым для последующего инженерного анализа полученных данных. Физическое время решения составляет 20 часов, объем занимаемой памяти 550 Гб. Таким образом, эффективный шаг интегрирования при моделировании обтекания с помощью DES метода может быть получен по следующей зависимости:
где 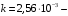 поправочный коэффициент для определения эффективного шага интегрирования. поправочный коэффициент для определения эффективного шага интегрирования.В результате работы получен эффективный шаг интегрирования по времени при моделировании с помощью DES метода на примере обтекания куба в программном пакете ANSYS. Определение временного шага по формуле (7) позволяет в разы сэкономить вычислительные ресурсы и физическое время расчета при сохранении решения с достаточным уровнем точности. Для достижения требуемого уровня сходимости следует постепенно уменьшать шаг интегрирования по времени или измельчать сетку в проблемной области расчета, приближаясь к числу Куранта 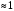 . .Анализ влияния числа Рейнольдса ( 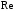 ), числа Маха ( ), числа Маха (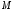 ) и числа Струхаля ( ) и числа Струхаля (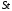 ) на изменение коэффициента ) на изменение коэффициента 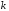 не проводился. не проводился. Список литературы 1. Методология CFX. ANSYS CFX-Solver Theory Guide, 2020 г. 2. Strelets M. Detached eddy simulation of massively separated flows, AIAA Paper, AIAA-2001-0879. 3. Shur M. L., Spalart P. R., Strelets M. K., Travin A. K. A hybrid RANS-LES approach with delayed-DES and wall-modeled LES capabilities, International Journal of Heat and Fluid Flow, 2008, 29, pp. 1638-1649. 4. Гарбарук А. В. Современные подходы к моделированию турбулентности: учеб. пособие / А. В. Гарбарук [и др.]. – СПб.: Изд-во Политехн. ун-та, 2016. – 234 с. 5. Белов Д. Турбулентность в CFD пакетах // Моделирование турбулентности – 28.02.2018. / [Электронный ресурс]. – Режим доступа: URL: https://issuu.com/denisruban/docs/lecture-3-turbulence_y_currant. 6. A. Gerasimov. Quick Guide to Setting Up LES-type simulations, version 1.4, May 2016. Available from ANSYS Customer Portal. 7. Пашков О.Л. Практические рекомендации по использованию метода крупных вихрей (LES) в ANSYS– 23.04.2015. / [Электронный ресурс]. – Режим доступа: URL: https://docplayer.ru/60716777 8. Spalart P.R. Young-Person's Guide to Deteched-Eddy Simulation Grids, NASA/CR-2001-211032, July 2001 9. Молчанов А.М. Построение сеток в задачах авиационной и космической техники: учеб. пособие / А. М. Молчанов, М. А. Щербаков, Д. С. Янышев, М. Ю. Куприков, Л. В. Быков; МАИ – Москва, 2013. – 260 с., с ил. 10. Патанкар С. Численные методы решения задач теплообмена и динамики надежности: Пер. с англ. М.: Энергоатомиздат, 1984. 11. Наум Я.В. Метод последовательных приближений / Под ред. Л.А. Пыжова, С.Д. Кайсера – М., 1968 г., 108 с. In the article the algorithm of the optimal step of the time-integrated example of the algorithm for external modeling of a cube in the DES (detached vortex method) method. Key words: integration step, DES, vortex counting method, mathematical modeling, computational fluid dynamics, Courant number. |