Лабараторная методичка. Определение характеристик источника постоянного тока
 Скачать 414.5 Kb. Скачать 414.5 Kb.
|
|
Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения» Кафедра «Физика»Л.Л. КоваленкоО.Ю. Пикуль ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ИСТОЧНИКА ПОСТОЯННОГО ТОКАМетодические указанияна выполнение лабораторной работы ХабаровскИздательство ДВГУПС 2007 УДК 53(075.8) ББК В 332 К 562 Коваленко, Л.Л. Определение характеристик источника постоянного тока: Методические указания на выполнение лабораторной работы / Л.Л. Коваленко, О.Ю. Пикуль. – Хабаровск: Изд-во ДВГУПС, 2007. – 16 с.: ил. Настоящие методические указания составлены на выполнение лабораторной работы по разделу "Электричество". В теоретической части выведены и сформулированы законы постоянного тока в дифференциальной и интегральной формах, в методе работы показано применение этих законов для определения основных характеристик источника постоянного тока, выполненного на базе понижающего трансформатора с полупроводниковым выпрямителем. В приложении дано описание принципа работы химического источника тока и приведена их классификация. Для студентов, успешно справившихся с обязательным заданием, предусмотрено дополнительное задание экспериментального характера. Работа рассчитана на два часа предварительной подготовки и на два часа выполнения в лабо-ратории. УДК 53(075.8) ББК В 332© ГОУ ВПО «Дальневосточный государственный университет путей сообщения» (ДВГУПС), 2007 ЦЕЛЬ РАБОТЫ Определить электродвижущую силу и ток короткого замыкания источника постоянного тока; исследовать зависимость полезной мощности источника от величины внешнего сопротивления. Приборы и принадлежности. Источник тока, вольтметр, амперметр, реостат, соединительные провода. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Характеристики электрического тока Упорядоченное движение свободных зарядов, возникающее в проводнике под действием электрического поля, называется током проводимости. В металлах могут свободно перемещаться только электроны. Направлением тока условились считать направление движения положительных частиц. Поэтому направление тока в металлах противоположно движению электронов. Линии, вдоль которых движутся заряженные частицы, названы линиями тока. Если внутри проводника с током мысленно выделить трубку, у которой боковая поверхность состоит из линий тока, то заряженные частицы при движении не будут пересекать боковую поверхность. Такая трубка называется трубкой тока. Поверхность металлической проволоки, находящейся в изоляторе, есть одна из трубок тока. Для количественной характеристики электрического тока вводятся основные величины: плотность тока и сила тока. Плотность тока равна величине заряда, проходящего в единицу времени через единицу поверхности, перпендикулярной к линиям тока Сила тока равна величине заряда, проходящего через всё поперечное сечение проводника в единицу времени. В металлах валентные электроны атома являются обобществленными, т.е. не принадлежащими определенному атому. Согласно электронной теории электропроводности Друде-Лоренца, такие электроны рассматриваются как электронный газ с зарядом каждого электрона 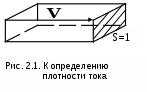 Выделим внутри проводника единичную площадку Выделим внутри проводника единичную площадку где Следовательно заряд, переносимый частицами в этом случае, будет равен плотности тока Вектор плотности тока совпадает по направлению со скоростью упорядоченного движения положительных зарядов. Величина силы электрического тока зависит от всей площади поперечного сечения проводника и определяется по формуле Если плотность тока и сила тока, протекающего по проводнику, не изменяется во времени, то такой ток называется постоянным. 2.2. Дифференциальная форма законов постоянного тока Упорядоченное движение электронов в металлическом проводнике возникает под действием внешнего электрического поля, напряженность которого ного пробега М 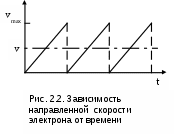 аксимальное значение направленной скорости определяется из формулы аксимальное значение направленной скорости определяется из формулы где Подставляя выражение (2.7) в формулу (2.4), получаемто есть закон Ома в дифференциальной форме. Коэффициент пропорциональности в этом законе называют удельной электропроводимостью, а и формулируется: плотность тока в проводнике равна произведению удельной электропроводимости металла на напряженность электрического поля. Электрическое поле совершает работу и ускоряет электроны в металлах. Накапливаемая ими энергия при столкновениях с ионами передается решетке и нагревает металл. Электронная теория электропроводности позволяет понять механизм выделения тепла электрическим током и вывести закон Джоуля-Ленца. Средняя кинетическая энергия электрона в начале свободного пробега равна Приращение энергии за счет работы электрических сил равно так как направление тепловой скорости u с одинаковой вероятностью может совпадать с направлением Преобразуем соотношение (2.12) с учетом формул (2.6) и (2.11) и получим Соотношение (2.13) представляет собой закон Джоуля-Ленца в дифференциальной форме: плотность тепловой мощности тока в проводнике равна произведению его удельной электропроводимости на квадрат напряженности электрического поля. Законы Ома (2.10) и Джоуля-Ленца (2.13) в дифференциальной форме справедливы для любых, в том числе и неоднородных, полей и проводников с переменными сечениями и электропроводимостями. 2.3. Интегральная форма законов постоянного тока Рассмотрим отрезок однородного цилиндрического проводника длиной 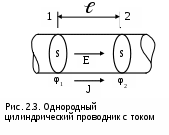 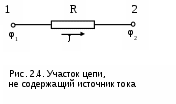 Для того чтобы в этом проводнике шел постоянный ток Сопротивление этого участка проводника определяется по формуле Используя закон Ома в дифференциальной форме (2.10) и соотношение (2.14), выразим силу тока, протекающего по проводнику, Полученное выражение Количество теплоты, выделяющееся в единицу времени на сопротивлении Используя закон Ома для участка цепи, формулу для мощности За конечный промежуток времени Формулы (2.18) и (2.19) являются математическим выражением закона Джоуля-Ленца в интегральной форме для мощности и количества теплоты соответственно. В замкнутой электрической цепи различают внешний  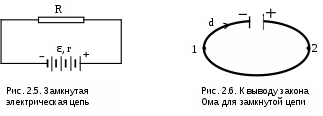 Основное назначение источника тока заключается в создании и поддержании разности потенциалов на его полюсах. Эта разность потенциалов возникает в результате действия сторонних сил Получим интегральную формулу закона Ома для замкнутой цепи. Обозначим через Перейдем от дифференциальных соотношений к интегральным. Рассмотрим замкнутую цепь, на участке 1-2 которой включен сторонний источник тока, как показано на рис. 2.6. Выделим мысленно малый элемент тока длиной Умножив обе части равенства на |
| | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
| | 0,6 | 0,72 | 0,9 | 1,02 | 1,14 | 1,26 | 1,38 | 1,5 | 1,62 | 1,8 | 1,92 | 2,04 |
| | | | | | | | | | | | | |
| | | | | | | | | | | | | |
КОНТРОЛЬНЫЕ ВОПРОСЫ
Что такое ток и плотность тока?
Закон Ома в дифференциальной форме.
Закон Джоуля-Ленца в дифференциальной форме.
Физический смысл ЭДС.
Дайте определение полной, полезной и потерь мощности.
При каком условии полезная мощность максимальна? Докажите.
Коэффициент полезного действия источника тока. Рассчитайте КПД при максимальной полезной мощности.
ПРИЛОЖЕНИЕ
7.1. Химические источники тока
К химическим источникам тока относятся гальванические элементы и аккумуляторы.
Рассмотрим ЭДС в гальваническом элементе. При погружении металлического электрода в электролит (водный раствор кислоты, щелочи или соли) часть атомов металла переходит в раствор в виде положительных ионов (рис. 7.1, а) сам же электрод оказывается при этом отрицательно заряженным. Между ним и электролитом возникает скачок потенциала. Но при этом усиливается и обратный процесс – переход положительных ионов из раствора. Нарастание потенциала прекратится, когда эти два процесса уравновесят друг друга, (рис. 7.1, а).
Если в электролит опустить еще один электрод, причем такой, который либо вообще не растворяется (уголь), либо растворяется слабо (медь), то около него скачок потенциала будет малым (рис.7.1, б) и между такими электродами образуется разность потенциалов, равная электродвижущей силе
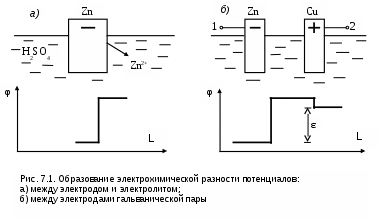
Если замкнуть цепь на нагрузку (соединить точки 1 и 2, рис.7.1, б), то возникнет ток как на внешнем, так и на внутреннем участках и падения напряжения на них
Однако для такого элемента не будет выполняться условие независимости
На рис. 7.2, а приведен распространенный гальванический элемент с деполяризатором – оксидом марганца, кристаллы которого насыпаны в пористый мешочек, окружающий угольный анод. В качестве электролита используется водный раствор хлорида аммония NH4СI, ионы NH4+ которого движутся к угольному, а ионы СI- – к цинковому электроду. Если специальной добавкой загустить электролит, а сам элемент плотно закрыть, получается так называемый сухой элемент. В качестве эталонной меры разности потенциалов используется нормальный элемент, (рис 7.2, б). Он дает
О


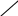
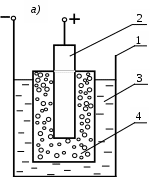
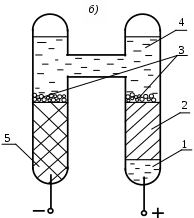
Рис. 7.2. Химические источники тока: а) гальванический элемент с деполяризатором (1 – цинковая оболочка (катод), 2 – угольный стержень (анод), 3 – электролит, 4 – деполяризатор); б) нормальный элемент (1 – ртуть, 2 – смесь серной кислоты H2SO4 и сульфата кадмия CdSO4, 3 – кристаллы той же соли CdSO4, 4 – насыщенный раствор того же сульфата CdSO4, 5 – амальгама кадмия, то есть сплав кадмия с ртутью).
писанные гальванические элементы – источники тока разового пользования. После того как их емкость израсходована, они не подлежат восстановлению. Если же в гальваническом элементе можно осуществить все химические реакции в обратном направлении, таким образом снова зарядив элемент, то получится устройство многоразового пользования, называемое аккумулятором. Классификация гальванических элементов и аккумуляторов осуществляется по химическому составу электродов и электролитов, по конструкции и форме. Химические источники имеют различную продолжительность работы, режим разряда и массу, широко используются в быту и в технике.
СПИСОК ЛИТЕРАТУРЫ
Калашников, С.Г. Электричество / С.Г. Калашников. – М. : Наука, 1982. – (с. 71–76)
Савельев, И.В. Курс общей физики / И.В. Савельев. – М. : Астрель, 2002. – Кн. 2 (с. 34–38).
Зисман, Г.А. Курс общей физики / Г.А. Зисман, О.М. Тодес. – М. : Наука, 1994. – Т. 2 (с. 20–24).
СОДЕРЖАНИЕ
1. ЦЕЛЬ РАБОТЫ ………………………… 3
2. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ ………………………… 3
2.1. Характеристики электрического тока ………………………….3
2.2. Дифференциальная форма законов постоянного тока………. 4
2.3. Интегральная форма законов постоянного тона………………..6
2.4. Нагрузочная способность источника тока ………..…………….. 9
3. МЕТОД РАБОТЫ ………………………...10
4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ ………………………. 12
5. ЗАДАНИЯ ПО УИРС …………………………12
6. КОНТРОЛЬНЫЕ ВОПРОСЫ …………………………13
7. ПРИЛОЖЕНИЕ …………………………13
7.1. Химические источники тока …………………………13
СПИСОК ЛИТЕРАТУРЫ …………………………15

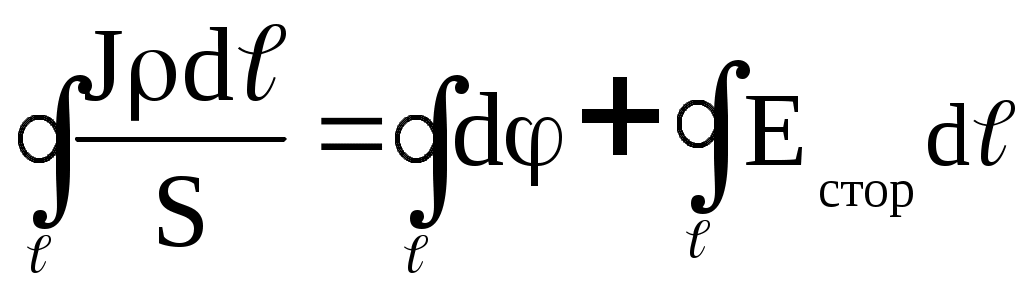 . (2.23)
. (2.23)
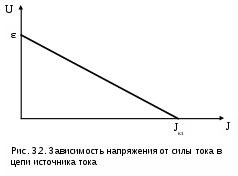 (рис. 3.2). Точки пересечения графика с осями координат определяют значения
(рис. 3.2). Точки пересечения графика с осями координат определяют значения