ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТВЁРДЫХ ТЕЛ ». Херовая лаба №18 (Мое исполенение). определение коэффициента теплопроводности твёрдых тел
 Скачать 178.45 Kb. Скачать 178.45 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра общей и технической физики Отчет по ЛАБОРАТОРНОЙ РАБОТЕ № 18 Тема: «ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ТВЁРДЫХ ТЕЛ » Выполнил: студент гр. ПЭ-21 _________ Тимофеев И.В. (шифр группы) (подпись) (Ф.И.О.) Проверил: руководитель работы: (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2021 Цель работы – определить коэффициент теплопроводности твердого тела методом сравнения с теплопроводностью эталонного образца из известного материала. Явление, изучаемое в работе: Теплопроводность. Определения основных физических понятий, процессов, величин: Если в термодинамической системе нарушить равновесие, например, нагревать одну из поверхностей пластины из теплопроводящего материала, то возникают необратимые (с точки зрения термодинамики) процессы. Если после прекращения внешнего воздействия предоставить систему самой себе, то возникает процесс релаксации, в результате которого система приходит в равновесное состояние. В случае, когда воздействие извне постоянно, неравновесное состояние сохраняется во времени, а возникшие процессы будут стационарны, т. е не зависящими от времени. К явлениям переноса: Нарушение равновесия приводит к переносу из одних мест среды в другие вещества (диффузия), импульса (вязкость), энергии или тепла (теплопроводность). Интенсивность процесса переноса характеризуется потоком той или иной величины. Поток любой физической величины это её количество, переносимое в единицу времени через воображаемую поверхность, перпендикулярно направлению переноса. Поток это скалярная физическая величина. Плотностью потокафизической величины называется ее количество, переносимое в единицу времени через единичную площадку, перпендикулярно направлению переноса. Законы и соотношения, описывающие изучаемые процессы, на основании которых получены расчетные формулы. Пояснения к физическим величинам и их единицам измерений: Теплопроводность. Для описания количества и направления переноса тепла вводится вектор плотности теплового потока (плотности потока энергии) 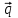 . Его направление совпадает с направлением переноса тепла (энергии), а величина определяется, как элементарное количество тепла dQ,переносимое в единицу времени через единицу поверхности . Его направление совпадает с направлением переноса тепла (энергии), а величина определяется, как элементарное количество тепла dQ,переносимое в единицу времени через единицу поверхности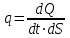 (1) (1)где dS - элемент площади, dt - интервал времени. Выравнивание температуры в системе сопровождается потоком тепла, плотность которого пропорциональна градиенту температуры в данной точке и определяется эмпирическим законом теплопроводности Фурье (Жан Батист Жозеф Фурье (1768 - 1830) – французский математик и физик). 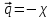 grad T или grad T или 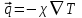 (2) (2)где 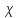 - коэффициент теплопроводности, grad T - градиент температуры, определяемый по формуле - коэффициент теплопроводности, grad T - градиент температуры, определяемый по формулеgrad T = 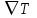 = = 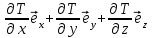 . (3) . (3) Проекции градиента температуры 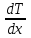 , ,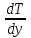 , ,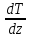 характеризуют изменение температуры по направлениям x, y, z. характеризуют изменение температуры по направлениям x, y, z.Направление градиента совпадает с направлением, вдоль которого температура растёт быстрее всего, т. е. с направлением, перпендикулярным к изотермам (линиям равной температуры). Коэффициент теплопроводности - физическая величина, характеризующая и численно равная плотности потока энергии при градиенте температуры равном единице. В случае одномерных явлений переноса, физические величины, определяющие эти явления, зависят только от одной координаты. В одномерном случае переноса тепла, например, вдоль координаты z, плотность потока тепла (энергии) определяется по формуле 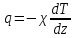 (4) (4)Поток тепла Q, переносимый через плоскую поверхность S 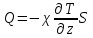 (5) (5)При цилиндрической симметрии, когда поток тепла направлен, например, перпендикулярно боковой поверхности цилиндра 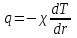 (6) (6)Плотность потока тепла и проекция градиента имеют противоположные знаки, так как энергия переносится в направлении убывания температуры. Температурное поле в плоском слое. Однородная плоская пластина толщиной d имеет температуру на одной поверхности Т1, на другой – Т2. Необходимо вывести зависимость для распределения температуры по толщине пластины в одномерном случае теплопереноса, т. е. получить формулу определяющую температурное поле в плоском слое. Градиент температуры внутри пластины (рис. 1) направлен перпендикулярно к ее свободным поверхностям, поскольку они являются поверхностями постоянной температуры. В том же направлении происходит перенос тепла. 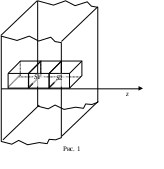 В установившемся стационарном режиме, т.е. при температуре, не изменяющейся со временем, через произвольные единичные поверхности S1 и S2 переносится одинаковое количество тепла в единицу времени, следовательно (в соответствии с (5)) получим 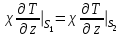 (7) (7)Поскольку пластина однородна, коэффициент теплопроводности величина постоянная для материала пластины 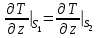 . .Поверхности S1 и S2 выбраны на произвольном расстоянии по глубине (по z), градиент температуры в данном случае не меняется по всей глубине т. е. 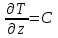 . . Интегрируя это равенство, получим, что температура изменяется линейно с глубиной 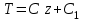 . (8) . (8)К 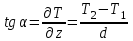 онстанты 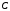 и и 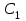 вычисляются используя граничные условия (условия на границах исследуемой области) на поверхностях пластины. По условию задачи и, учитывая полученное выражение (8), при z = 0 (на поверхности пластины), вычисляются используя граничные условия (условия на границах исследуемой области) на поверхностях пластины. По условию задачи и, учитывая полученное выражение (8), при z = 0 (на поверхности пластины), 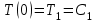 . Далее, поскольку градиент температуры постоянен, и при z = d температура второй поверхности пластины по условию . Далее, поскольку градиент температуры постоянен, и при z = d температура второй поверхности пластины по условию 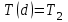 , следует, что , следует, что 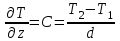 . . Окончательно распределение температуры внутри пластины 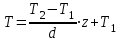 (9) (9)График изменения температуры приведен на рис.2. Основные расчетные формулы: Перепад температур на исследуемой пластине: dT2 = (T2- T3), где T3- температура холодильника , T2-температура между пластинами Перепад температур на эталонной пластине: dT1 = (T1 - T2), где T1 - температура нагревателя , T2-температура между пластинами Коэффициент теплопроводности исследуемой пластины : 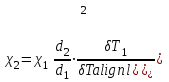 , где dT1 и dT2 - перепады температур на пластинках, dT1 = (T1 - T2) - перепад температур на эталонной пластине, dT2 = (T2- T3) -перепад температур на исследуемой пластине, d1 и d2 – толщины пластин. , где dT1 и dT2 - перепады температур на пластинках, dT1 = (T1 - T2) - перепад температур на эталонной пластине, dT2 = (T2- T3) -перепад температур на исследуемой пластине, d1 и d2 – толщины пластин.Исходные данные: Материал эталонной пластины: свинец Материал исследуемой пластины: алюминий d1= 4 мм=0.004 м d2= 7 мм=0.007 м χ1= 34.9 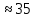 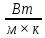 Погрешности прямых измерений: 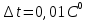 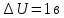 Погрешность косвенных измерений : 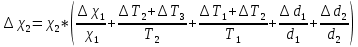 = =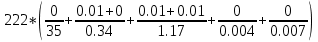 =10 =10 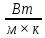   = =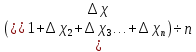 = ==(60+70+21+15+10+7+5+4) 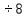 =20 =20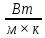 Таблица 1. Результаты измерений и вычислений
dT2 = (T2- T3) =20.01-20=0.01 dT1 = (T1 - T2) =20.06-20.01=0.05 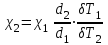 =35 =35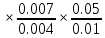 =306 =306 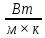  = =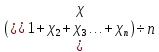 =(306+232+209+203+205+210+207+208) =(306+232+209+203+205+210+207+208)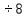 =222 =222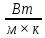 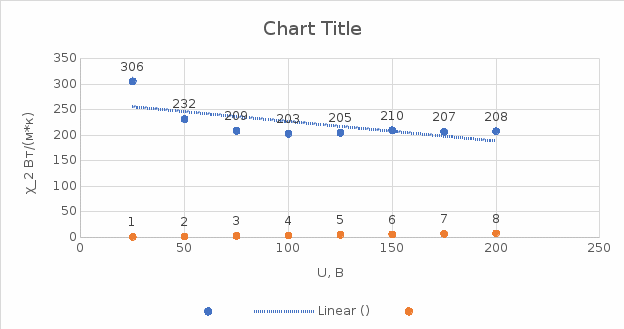 Результат Коэффициент теплопроводностиэкспирементальный с учетом погрешности вычмслений: 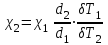 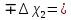 232 232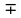 10.04 10.04 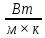 Коэффициент теплопроводностиэкспирементальный средний с учетом погрешности вычмслений: 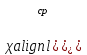 = =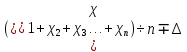 =222 =222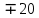 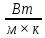 Сравнительная оценка результатов %= 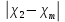 / /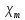 *100% = |222-209|/209*100% *100% = |222-209|/209*100% 6% 6%Вывод Из графика следует, что среднее значение коэффициента теплопроводности свинца равно 222 (Втм∗К). В справочниках это значение 209 Вт/(м*К). Способом, который мы применили в данной лабораторной работе, можно определить коэффициент теплопроводности вещества с относительной погрешностью около 6%. Это можно исправить, проведя большее количество измерений или взяв более точное оборудование . |