Определение коэффициента внутреннего трения в жидкости по методу стокса

• Название: Определение коэффициента внутреннего трения в жидкости по методу стокса
• Дата: 15.10.2022
• Размер: 147.5 Kb.
• Имя файла: umm_8.doc
• Тип: Методические указания; #735479

Министерство образования и науки Российской Федерации

Волгоградский государственный технический университет

Институт архитектуры и строительства

Кафедра физики


ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ В ЖИДКОСТИ ПО МЕТОДУ СТОКСА


Методические указания к лабораторной работе №8


Волгоград 2013
УДК 537.21 (076.5)

Определение коэффициента внутреннего трения в жидкости методом Стокса: Метод. указания к лабораторной работе / Сост. Л.И. Черкасова; ВолгГАСА. -Волгоград, 2002, 10 с.

Целью работы является определение внутреннего трения в жидкости методом Стокса. Приводится краткая теория явления стационарной теплопроводности. Дано описание экспериментальной установки, описан порядок выполнения работы, расчета и графического представления результатов, сформулировано задание для учебно-исследовательской работы. Даны правила техники безопасности и приведены контрольные вопросы.

Для студентов всех специальностей по дисциплине «Физика».

Ил. 1. Табл. 1. Библиогр. 1 назв.


© Волгоградская государственная архитектурно-строительная академия, 2002

© Составление Черкасова Л.И., Жога Л.В., 2002





Цель работы: Определить коэффициент внутреннего трения в исследуемой жидкости по измеренной скорости падения шарика в ней.
Приборы и принадлежности: Стеклянный цилиндр с исследуемой жидкостью, микрометр, секундомер, масштабная линейка, свинцовые шарики.
Теоретическое введение

Явлением внутреннего трения (вязкостью) называется появление сил трения f_тр между слоями газа или жидкости, движущимися относительно друг друга параллельно с различными по величине скоростями. Вследствие обмена молекулами за счет их хаотического теплового движения более быстрый слой ускоряет соседний с ним медленный слой, и, наоборот, медленный слой задерживает более быстрый. Силы внутреннего трения направлены по касательным к слоям газа или жидкости.

Скорость беспорядочного теплового движения молекул V в текущем газе (или жидкости) в среднем одинакова во всех точках рассматриваемого пространства, но скорость направленного движения одинакова только для молекул данного слоя газа (или жидкости) и различна для различных слоев. Молекулы, перелетая, благодаря тепловому движению, из более быстрого слоя в медленный, приносят с собой большую, чем в медленном слое, составляющую импульса направленного движения mU₂ и тем самым ускоряют медленный слой. Наоборот, молекулы, попадающие из медленного слоя в более быстрый, имеют меньшую составляющую импульса mU₁, в результате чего они уменьшают скорость более быстрого слоя.

Мысленно выделим в газе площадку 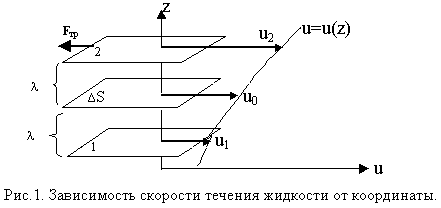(рис.1), параллельную слоям, текущим с различными скоростями U.







Пусть слой 1 лежит под площадкой ΔS на расстоянии средней длины свободного пробега молекул . Тогда молекулы, летящие из слоя 1 по направлению к площадке ΔS, достигнут ее без столкновений. Число молекул Δn, пролетающих через площадку ΔS за время t из слоя 1:

, (1)

где V - средняя скорость теплового движения молекул, n₀ – число молекул в единице объема. Множитель 1/6 учитывает равновероятность движения молекул обоих направлений каждой из координатных осей.

Такое же количество молекул из слоя 2 пересекает площадку S в противоположном направлении. Но, поскольку скорости U₁ и U₂ слоев 1 и 2 различны, то в прямом и обратном направлениях будут перенесены различные импульсы К₁ и К₂направленного движения:

, (2)

, (3)

где m- масса молекулы.

В результате этих двух переносов импульса, происходящих в противоположных направлениях, через площадку ΔS будет перенесен от слоя 2 к слою I импульс

. (4)

Разность абсолютных величин скоростей U₂ -U₁, можно выразить через градиент скорости U. Градиент скорости есть величина, численно равная изменению величины скорости движения слоев на единицу длины в направлении, перпендикулярном поверхности слоя. Для нашего случая градиент скорости равен , где dZ=2 (см. рис.1).

Тогда разность U₂-U₁ равна градиенту скорости, умноженному на расстояние между слоями I и 2, т.е. на 2.

, (5)

следовательно (4) принимает вид

. (6)

Замечая, что n₀m есть плотность газа , получим

. (7)

Сила внутреннего трения f_тр (рис.1), действующая со стороны более медленного слоя 1 на более быстрый слой 2, согласно второму закону Ньютона равна приращению импульса слоя 2 в единицу времени

. (8)

Введем обозначение

. (8а)

Тогда

. (9)

Сила внутреннего трения, возникающего при макроскопических движениях в газе или жидкости, прямо пропорциональна градиенту скорости. Коэффициент пропорциональности  носит название коэффициента внутреннего трения, или динамического коэффициента вязкости.

Коэффициент вязкости (или динамическая вязкость) численно равен силе внутреннего трения, действующей на единицу площади границы раздела параллельно движущихся слоев газа или жидкости, когда скорость их движения изменяется на единицу при перемещении на единицу длины в направлении, перпендикулярном к границе раздела.

Закон (9) был получен Ньютоном из анализа экспериментальных данных и явился основой для изучения движения вязкой жидкости и газа.

Коэффициент вязкости зависит от температуры. Кинетическая теория идеального газа дает следующие выражения для входящих в формулу (8a) величин:

- средняя длина свободного пробега молекулы,

где n₀ - число молекул в единице объема, - эффективное сечение молекулы.

- средняя квадратичная скорость движения молекулы,

где К - постоянная Больцмана, Т - абсолютная температура,m - масса молекулы.

Кроме того, плотность =mn₀.

Подставив все эти выражения в (8a), получим

, (10)

т.е. вязкость идеального газа возрастает с ростом температуры.

В жидкости сила трения между слоями описывается тем же уравнением (9), что и в газе, но коэффициент вязкости уменьшается при повышении температуры. Это объясняется тем, что в отличие от идеального газа между молекулами жидкости имеются значительные силы притяжения. Вследствие этого молекулы жидкости большую часть времени находятся около положений равновесия, и перескок молекулы становится возможным при разрыве межмолекулярной связи. С ростом температуры доля молекул, имеющих связи, уменьшается, в результате чего текучесть жидкости возрастает, а вязкость падает.

Зависимость коэффициента вязкости жидкости от температуры описывается формулой Френкеля

, (1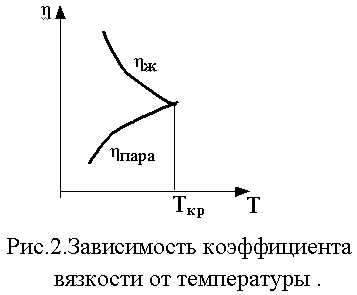1)

г

де W– энергия, которую нужно сообщить молекуле жидкости, чтобы она могла перескочить из одного положе-ния равновесия в соседнее. Величина W имеет порядок (2 3)10^-20Дж, причем W>0. Вязкость жидкости обычно во много раз больше, чем у газа. С ростом температуры вязкость жидкости экспоненциально уменьшается, а вязкость пара возрастает пропор-ционально , и при критической температуре T_кр они становятся одинаковыми (рис. 2).

Таблица 1

Вязкость некоторых жидкостей при различных температурах

Вещество	Температура, 0С	Вязкость, Нсм-2
Вода	0 20 50 100	1,1910-3 1,0510-3 0,5510-3 0,2810-3
Ртуть	0 20 100	1,6810-3 1,5510-3 1,2410-3
Глицерин	0 20 50 100	13,40 12,1 1,49 0,629

Тела, движущиеся в вязкой жидкости или газе, испытывают сопротивление. Сила сопротивления, испытываемая шаром, прямо пропорциональна вязкости газа (жидкости) , радиусу шара r и скорости его движения V.

. (12)

Формула (12) носит название закона Стокса и применима лишь для тел достаточно малых размеров и малой скорости движения относительно жидкости. Сила сопротивления движению шара в жидкости возникает из-за сил внутреннего трения при течении слоев жидкости, движущихся вместе с шаром, относительно слоев, остающихся неподвижными. Закон Стокса, как и закон Ньютона для вязкости, применим, если течение жидкости ламинарное, т.е. такое, при котором каждый выделенный слой скользит параллельно соседним, не перемешиваясь с ними. Ламинарное течение наблюдается при малых скоростях.

При возрастании скорости в жидкости возникает интенсивное вихреобразование и перемешивание. Такое течение называется турбулентным или вихревым. В этом случае сила сопротивления становится пропорциональной квадрату скорости.

Характер течения жидкости определяется безразмерным числом Рейнольдса:

, (13)

где r- величина, характеризующая линейные размеры тела, обтекаемого жидкостью (газом),V - скорость течения, ρ - плотность жидкости (газа), - динамическая вязкость.

Если при данных условиях число Re превышает определенное критическое значение, то поток становится турбулентным; при значениях Reменьших критического - ламинарным. Таким образом, число Рейнольдса можно использовать в качестве критерия применимости закона Стокса. Для шарика критическим является Re =0,5.

Рассчитаем по формуле (13) число Рейнольдса для движения шарика в глицерине при условии: = 1200 кг/м³ , r =1мм = 10 ^-3м , V = 0,2 м/с , η =0,8 кг/м.с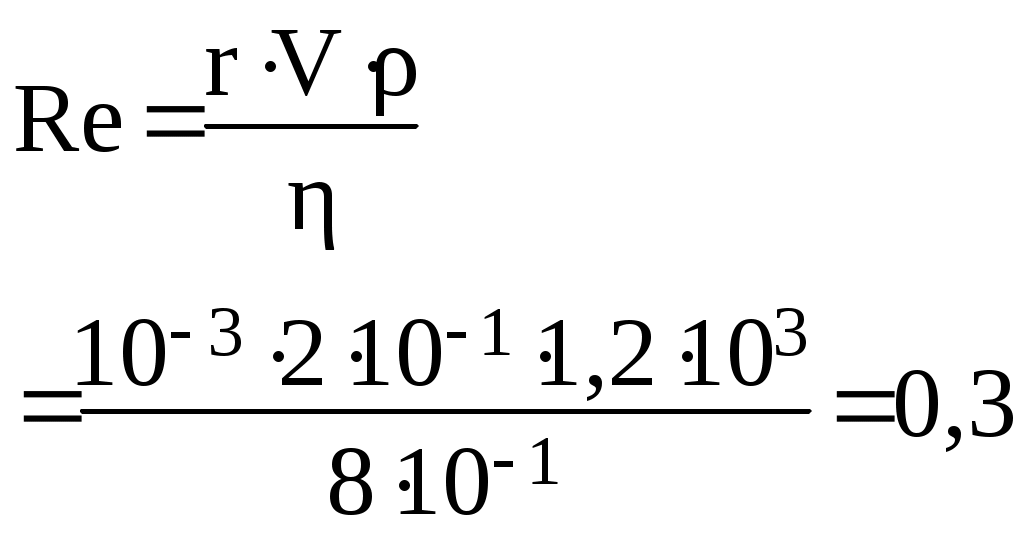


,
Re


Так как числоRe оказалось меньше 0,5, то закон Стокса в этих условиях применим. Подобные условия должны осуществляться в нашем опыте.

Метод измерения

Коэффициент вязкости в работе определяется с помощью наполненного исследуемой жидкостью вертикального стеклянного цилиндра с двумя горизонтальными метками А и А₁, расположенными друг от друг расстоянии l (рис. 3). Если в исследуемой жидкости падает шарик небольших размеров, то на него действуют три силы: сила тяжести mg, выталкивающая сила F_арх и сила сопротивления, обусловленная вязкостью жидкости f_тр. Силу тяжести можно выразить через плотность шарика ρ и его радиус r

. (14)

Выталкивающая сила Архимеда равна

, (15)

где ₁ – плотность жидкости.

Сила сопротивления f_тр определяется по закону Стокса (12).

Все три силы направлены по вертикали: сила тяжести - вниз, выталкивающая сила и сила сопротивления (трения) - вверх (см. рис. 3).

П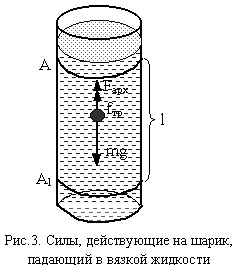

усть в начальный момент времени скорость шарика равна нулю и, следовательно, равна нулю сила трения. Так как сила тяжести больше выталкивающей силы, шарик будет падать ускоренно до тех пор, пока с увеличением скорости сила трения не возрастает настолько, что в сумме с выталкивающей силой станет равной силе тяжести. Равнодействующая трех сил станет равной нулю.

     (16)

Шарик при этом начнет двигаться с постоянной скоростью V .
Учитывая (3), (4), (5), получим

. (17)

Решая это уравнение относительно :


или
, (18)

где скорость установившегося движения; l - расстояние, пройденное шариком;t - время падения шарика; D – диаметр шарика.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. 
   Установите верхнюю метку на трубке с исследуемой жидкостью на 3-6 см ниже уровня жидкости, чтобы шарик при падении проходил ее с установившейся скоростью. Нижнюю метку установите на расстоянии 3-6 см от дна трубки и измерьте расстояние между метками по масштабной линейке, укрепленной на трубке.
   
2. 
   Измерьте 3 раза диаметр шарика микрометром и найдите его среднее значение.
   
3. 
   Опустите шарик в жидкость и секундомером измерьте время прохождения шариком расстояния l между метками.
   
4. 
   По формуле (18) определите коэффициент вязкости. Вычисления необходимо проводить в системе СИ. Опыт повторите 8 раз, найдите среднее значение _ср.
   
5. 
   По методу Стьюдента вычислите ошибку  при W = 0,95. Все результаты запишите в таблицу 2.
   

Таблица 2

Реультаты имерений

N

D1 мм

D2 мм

D3 мм

Dср мм

l i см

ti с

i Нс/м2

ср Нс/м2

i Нс/м2

(i)2 Нс/м2

(i)2 Нс/м2

 Нс/м2

ср Нс/м2

1

…

8

Задание к УИРС. Исследуйте зависимость коэффициента вязкости жидкости от температуры.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. 
   Чему равна и как направлена сила внутреннего трения двух слоев жидкости?
   
2. 
   Каков физический смысл коэффициента вязкости? Размерность его.
   
3. 
   Объясните возникновение сил внутреннего трения с точки зрения молекулярно-кинетической теории. Дайте вывод формулы для силы внутреннего трения.
   
4. 
   Как зависит от температуры коэффициент вязкости для газа и жидкости? Объясните разницу.
   
5. 
   Запишите формулу Стокса и объясните, при каких условиях ею можно пользоваться.
   
6. 
   Дайте понятия ламинарного и турбулентного течений.
   
7. 
   Оцените число Рейнольдса по вашим данным, используя измерения для самого большого и самого маленького шариков и среднее значение найденного коэффициента вязкости.
   

лИТЕРАТУРА

Трофимова Т. И. Курс общей физики . М.: Высш.шк. 1994

План учеб.-метод. Документ. 2002 г., поз.30

Подписано в печать .10.02. Формат 60х48/16.

Бумага офсетная. Гарнитура Таймс.

Усл. печ. л. 0,65. Уч. изд. л. 0,7. Тираж 100 экз. Заказ № .
Волгоградская государственная архитектурно-строительная академия

Редакционно-издательский отдел

Сектор оперативной полиграфии ЦИТ

400074, Волгоград, ул. Академическая, 1