Ответы на экзаменационные вопросы. вопросы экзамен тепломас обмен. Закон Фурье. Температурным полем называют совокупность мгновенных значений температуры во всех точках рассматриваемого пространства
 Скачать 4.69 Mb. Скачать 4.69 Mb.
|
1 2 1)Температурное поле. Температурный градиент. Тепловой поток. Плотность теплового потока. Закон Фурье. Температурным полем называют совокупность мгновенных значений температуры во всех точках рассматриваемого пространства. Градиент температуры. Производная температуры по нормали к изотермической поверхности называется градиентом температуры: Тепловой поток – это поток энергии (в форме теплоты), обусловленный ее самопроизвольным, необратимым переносом в пространстве от более нагретых тел (участков тела) к менее нагретым. Плотность теплового потока:  Закон Фурье  2)Коэффициент теплопроводности. Условия однозначности для процессов теплопроводности. Коэффициент теплопроводности– это физический параметр вещества, который в общем случае зависит от температуры, давления и природы вещества.  3)Передача теплоты через однослойную плоскую стенку при граничных условиях I и III рода (теплопередача). Граничные условия первого рода, в которых задается распределение температуры на поверхности тела для каждого момента времени: tc = f(x, y, z, ); частный случай tc = const Граничные условия третьего рода, в которых задается температура окружающей среды tж и закон теплообмена между поверхностью тела и окружающей средой в процессе охлаждения и нагревания. Для его описания используется закон Ньютона – Рихмана: плотность теплового потока пропорциональна разности температур поверхности тела tc и окружающей среды tж: q = (tc – tж). Здесь – коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой. Численно равен количеству тепла, отдаваемому (воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью и средой в один градус. Теплопередачей называется передача теплоты от горячего теплоносителя к холодному теплоносителю через стенку, разделяющую эти теплоносители. Примерами теплопередачи являются: передача теплоты от греющей воды нагревательных элементов (отопительных систем) к воздуху помещения; передача теплоты от дымовых газов к воде через стенки кипятильных труб в паровых котлах; передача теплоты от раскаленных газов к охлаждающей воде (жидкости) через стенку цилиндра двигателя внутреннего сгорания; передача теплоты от внутреннего воздуха помещения к наружному воздуху и т. д. При этом ограждающая стенка является проводником теплоты, через которую теплота передается теплопроводностью, а от стенки к окружающей среде конвекцией и излучением. Поэтому процесс теплопередачи является сложным процессом теплообмена. П 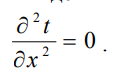 ри установившемся, или стационарном, тепловом режиме температура тела не зависит от времени. Рассмотрим однородную и изотропную стенку толщиной с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживаются постоянными температуры tc1 и tc2. Дифференциальное уравнение теплопроводности для рассматриваемого случая запишется в виде ри установившемся, или стационарном, тепловом режиме температура тела не зависит от времени. Рассмотрим однородную и изотропную стенку толщиной с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживаются постоянными температуры tc1 и tc2. Дифференциальное уравнение теплопроводности для рассматриваемого случая запишется в виде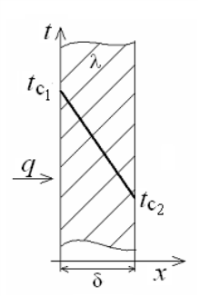 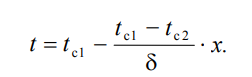 Граничные условия в данной задаче зададим следующим образом: при х = 0 t = tc1; при х = t = tc2. Закон распределения температуры по толщине стенки найдем, дважды проинтегрировав уравнение и найдя константы интегрирования из граничных условий, заданных уравнениями Граничные условия в данной задаче зададим следующим образом: при х = 0 t = tc1; при х = t = tc2. Закон распределения температуры по толщине стенки найдем, дважды проинтегрировав уравнение и найдя константы интегрирования из граничных условий, заданных уравнениями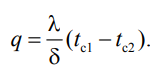 Для определения количества тепла, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, воспользуемся законом Фурье, согласно которому / xtq . Для определения количества тепла, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, воспользуемся законом Фурье, согласно которому / xtq . Из уравнения следует, что количество тепла, проходящее через единицу поверхности в единицу времени прямо пропорционально коэффициенту теплопроводности и температурному напору и обратно пропорционально толщине стенки. Отношение / называется тепловой проводимостью стенки, а обратная величина / – тепловым или термическим сопротивлением стенки. Последнее представляет собой падение температуры в стенке на единицу плотности теплового потока. Зная удельный тепловой поток, легко вычислить общее количество тепла, которое передается через поверхность стенки величиной F за промежуток времени : Из уравнения следует, что при прочих равных условиях температура в стенке убывает тем быстрее, чем больше плотность теплового потока. Если отсчет избыточной температуры в стенке вести от наименьшей заданной температуры tc2, то уравнение можно привести к безразмерному виду Уравнение температурного поля является универсальным, так как распределение температуры в стенке можно представить единой прямой для любых заданных значений температур стенки tc1, tc2 и ее толщины Выражения и получены в предположении, что коэффициент теплопроводности является постоянной величиной. В действительности это не всегда бывает так. Рассмотрим зависимость коэффициента теплопроводности только от температуры, которая для многих материалов близка к линейной 0 (1 ) bt , где 0 – значение коэффициента теплопроводности при 0о С. Тогда плотность теплового потока на поверхности пластины Из этого уравнения следует, что температура в стенке изменяется не линейно, а по кривой. Характер температурной кривой определяется знаком и численным значением коэффициента b В  опрос 4. Передача теплоты через многослойную плоскую стенку при граничных условиях 1 и 3 рода (теплопередача) опрос 4. Передача теплоты через многослойную плоскую стенку при граничных условиях 1 и 3 рода (теплопередача)Рассмотрим теплопроводность многослойной стенки состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях двух слоев одинакова. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки П 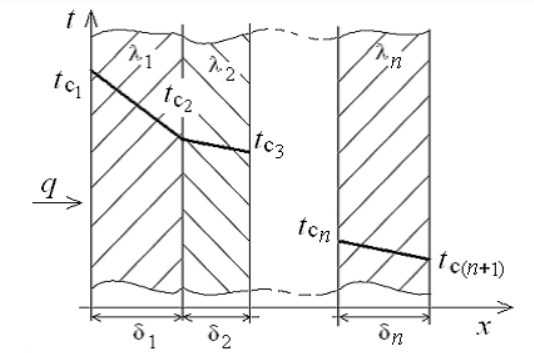 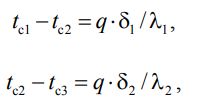 ри заданных температурах внешних поверхностей такой стенки, размерах слоев и, соответственно, коэффициентах теплопроводности можно составить систему уравнений для плотности теплового потока каждого из слоев, из которых выразим температурные напоры ри заданных температурах внешних поверхностей такой стенки, размерах слоев и, соответственно, коэффициентах теплопроводности можно составить систему уравнений для плотности теплового потока каждого из слоев, из которых выразим температурные напорыО 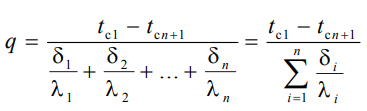 тсюда плотность теплового потока тсюда плотность теплового потокав 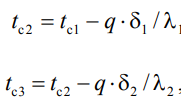 еличина , равная сумме тепловых сопротивлений всех n слоев, называется полным тепловым или термическим сопротивлением теплопроводности многослойной стенки. Температуры на границе соприкосновения двух соседних слоев равны еличина , равная сумме тепловых сопротивлений всех n слоев, называется полным тепловым или термическим сопротивлением теплопроводности многослойной стенки. Температуры на границе соприкосновения двух соседних слоев равныТемпературы на границе соприкосновения двух соседних слоев равны Внутри каждого из слоев температура изменяется согласно уравнениям или для многослойной стенки в целом температурная кривая представляет ломаную линию. При сравнении переноса тепла через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности для многослойной стенки экв. Он равен коэффициенту теплопроводности однородной стенки, толщина которой равна толщине многослойной стенки Т 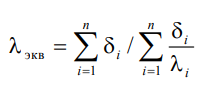 аким образом, эквивалентный коэффициент теплопроводности экв зависит не только от теплофизических свойств слоев, но и от их толщины. аким образом, эквивалентный коэффициент теплопроводности экв зависит не только от теплофизических свойств слоев, но и от их толщины.П 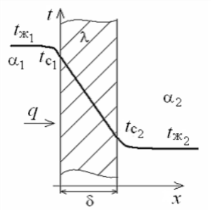 ередача тепла от одной жидкой среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде ередача тепла от одной жидкой среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной подвижной среде Пусть плоская однородная стенка имеет толщину Заданы коэффициент теплопроводности , температуры окружающей среды tж1 и tж2, а также коэффициенты теплоотдачи 1 и 2. Будем считать, что tж1, tж2, 1 и 2 постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки. При заданных условиях необходимо найти тепловой поток от горячей жидкости к холодной, а также температуры на поверхностях стенки. Удельный тепловой поток от горячей жидкости к стенке определяется из закона Ньютона – Рихмана уравнением П Э А 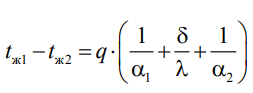 налогично решению для многослойной плоской стенки выразим температурные напоры и почленно сложим правые и левые части, тогда налогично решению для многослойной плоской стенки выразим температурные напоры и почленно сложим правые и левые части, тогдаВ 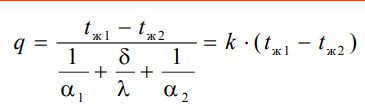 ыразим плотность теплового потока ыразим плотность теплового потока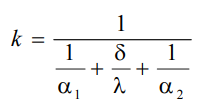 Здесь коэффициент теплопередачи, характеризующий интенсивность передачи тепла от одной жидкости к другой через разделяющую их стенку, имеет ту же размерность, что и коэффициент теплоотдачи, численно равен количеству тепла, которое передается через единицу поверхности стенки в единицу времени при разности температур между жидкостями в один градус. Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением теплопередачи и для однослойной стенки запишется как  Вопрос 5. Передача теплоты через однослойную цилиндрическую стенку при граничных условиях 1 и 3 рода. Критический диаметр цилиндрической стенки Р 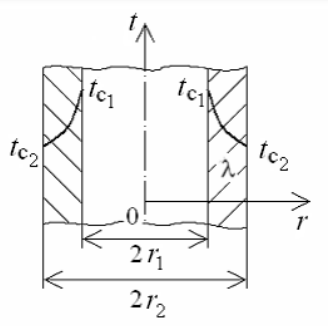 у Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. В случае плоской стенки удельный тепловой поток q остается одинаковым для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянную величину. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность будет величиной переменной, так как величина поверхности зависит от радиуса Д 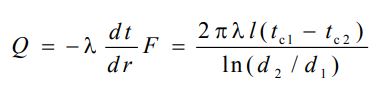 ля определения количества теплоты, проходящего через цилиндрическую поверхность величиной F 2 r l в единицу времени, следует воспользоваться законом Фурье ля определения количества теплоты, проходящего через цилиндрическую поверхность величиной F 2 r l в единицу времени, следует воспользоваться законом ФурьеТепловой поток через единицу внутренней поверхности Т Т 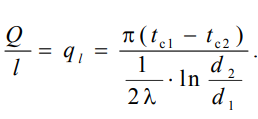 епловой поток на единицу длины трубы епловой поток на единицу длины трубы Тепловой поток, отнесенный к единице длины трубы, имеет размерность Вт/м и называется линейной плотностью теплового потока Критический диаметр цилиндрической стенки Рассмотрим влияние изменения наружного диаметра d2 на термическое сопротивление однородной цилиндрической стенки. При постоянных значениях 1, 2, и d1 полное термическое сопротивление теплопередачи цилиндрической стенки будет зависеть только от внешнего диаметра. При этих условиях термическое сопротивление теплоотдачи на внутренней поверхности цилиндра Термическое сопротивление теплопроводности термическое сопротивление теплоотдачи на наружной поверхности цилиндра О З П 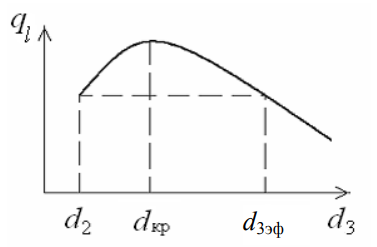 ри d2 < dкр с увеличением d2 полное термическое сопротивление теплопередачи падает, так как увеличение наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки. ри d2 < dкр с увеличением d2 полное термическое сопротивление теплопередачи падает, так как увеличение наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки. При d2 > dкр с увеличением d2 термическое сопротивление теплопередачи возрастает, что указывает на доминирующее влияние толщины стенки. Изложенные соображения необходимо учитывать при выборе тепловой изоляции различных цилиндрических аппаратов и трубопроводов. Рассмотрим критический диаметр изоляции, наложенной на трубу. Термическое сопротивление теплопередачи для такой трубы 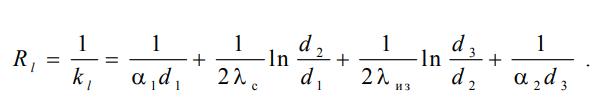 В Е 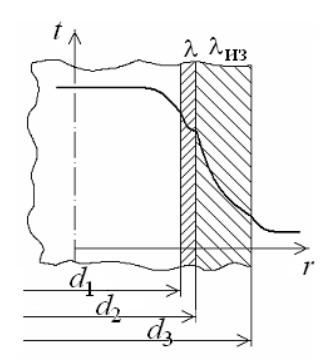 сли окажется, что величина dкр.из больше наружного диаметра трубы d2, то применение выбранного материала в качестве тепловой изоляции в области d2 < d3 < dкр.из приведет к тому, что при увеличении толщины изоляции будет наблюдаться увеличение потерь тепла. Только при d3 = dэф потери тепла вновь станут такими же, как для первоначального, неизолированного трубопровода сли окажется, что величина dкр.из больше наружного диаметра трубы d2, то применение выбранного материала в качестве тепловой изоляции в области d2 < d3 < dкр.из приведет к тому, что при увеличении толщины изоляции будет наблюдаться увеличение потерь тепла. Только при d3 = dэф потери тепла вновь станут такими же, как для первоначального, неизолированного трубопровода Следовательно, некоторый слой тепловой изоляции не будет оправдывать своего назначения. Таким образом, для эффективной работы тепловой изоляции необходимо, чтобы dкр.из d2 Вопрос 6. Передача теплоты через многослойную цилиндрическую стенку при граничных условиях 1 и 3 рода. Р 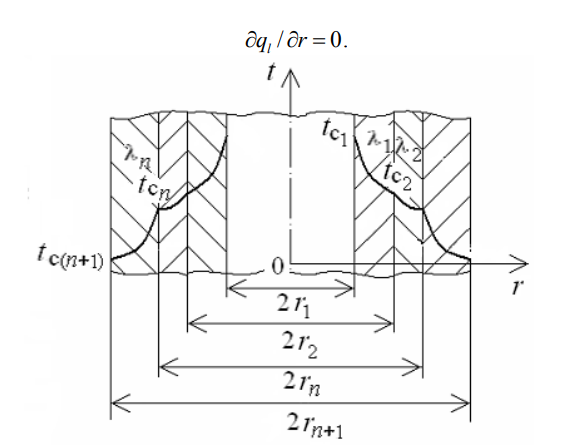 ассмотрим теплопроводность многослойной цилиндрической стенки, состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях соседних слоев одинакова. Заданы температуры на внешних поверхностях стенки, коэффициенты теплопроводности и толщины слоев (рис. 4.2). Метод решения аналогичен методу для плоской многослойной стенки. При стационарном тепловом режиме линейная плотность теплового потока не меняется по толщине стенки ассмотрим теплопроводность многослойной цилиндрической стенки, состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях соседних слоев одинакова. Заданы температуры на внешних поверхностях стенки, коэффициенты теплопроводности и толщины слоев (рис. 4.2). Метод решения аналогичен методу для плоской многослойной стенки. При стационарном тепловом режиме линейная плотность теплового потока не меняется по толщине стенки  Составим систему уравнений линейных плотностей теплового потока для каждого из слоев. Выразим из них температурные напоры и почленно сложим уравнения, тогда Составим систему уравнений линейных плотностей теплового потока для каждого из слоев. Выразим из них температурные напоры и почленно сложим уравнения, тогда Отсюда линейная плотность теплового потока Отсюда линейная плотность теплового потока  В 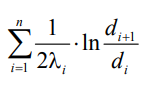 еличина называется линейным термическим сопротивлением теплопроводности отдельного слоя, а величина еличина называется линейным термическим сопротивлением теплопроводности отдельного слоя, а величина п 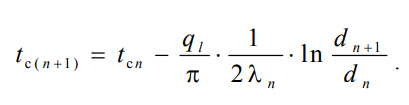 редставляет собой термическое сопротивление всех слоев и называется полным линейным термическим сопротивлением теплопроводности многослойной цилиндрической стенки. Температура на границе соприкосновения любых слоев редставляет собой термическое сопротивление всех слоев и называется полным линейным термическим сопротивлением теплопроводности многослойной цилиндрической стенки. Температура на границе соприкосновения любых слоев Внутри любого слоя температура изменяется по логарифмической кривой П 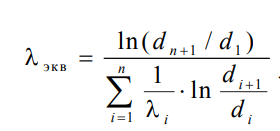 Отсюда эквивалентный коэффициент теплопроводности Рассмотрим однородную цилиндрическую стенку (трубу) с внутренним диаметром d1 и наружным диаметром d2 с постоянным коэффициентом теплопроводности . Заданы постоянные температуры подвижных сред tж1 и tж2, а также постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы 1 и 2. Необходимо найти температуры поверхностей цилиндрической стенки tс1 и tс2 и тепловой поток через нее 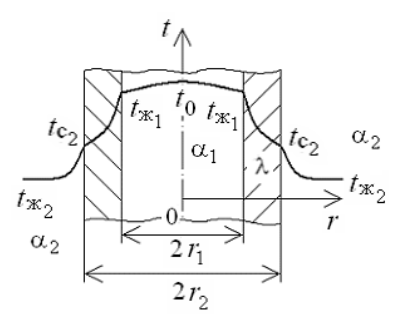 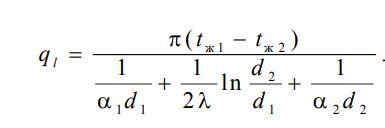 Тогда линейная плотность теплового потока определяется как Тогда линейная плотность теплового потока определяется как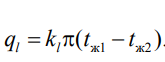 Величина k называется линейным коэффициентом теплопередачи. Она характеризует интенсивность передачи тепла от одной подвижной среды к другой через разделяющую их стенку. Значение k численно равно количеству тепла, которое проходит через стенку трубы длиной один метр в единицу времени от одной жидкой среды к другой при разности температур между ними в один градус. Величина Rl /1 kR , обратная коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи: В 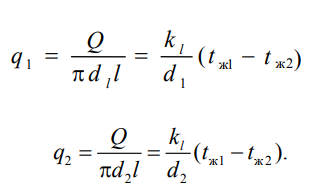 отличие от термических сопротивлений теплоотдачи для плоской стенки здесь термические сопротивления теплоотдачи зависят не только от коэффициента теплоотдачи, но и от диаметра стенки. Если тепловой поток через цилиндрическую стенку отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, отнесенную к единице соответствующей поверхности трубы отличие от термических сопротивлений теплоотдачи для плоской стенки здесь термические сопротивления теплоотдачи зависят не только от коэффициента теплоотдачи, но и от диаметра стенки. Если тепловой поток через цилиндрическую стенку отнести к внутренней или наружной поверхности стенки, то получим плотность теплового потока, отнесенную к единице соответствующей поверхности трубы Т 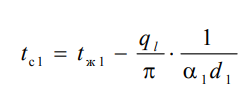 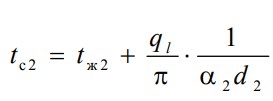 емпературы поверхностей цилиндра емпературы поверхностей цилиндра В В 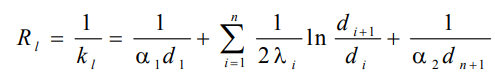 еличина Rl называется полным термическим сопротивлением теплопередачи многослойной цилиндрической стенки и равна еличина Rl называется полным термическим сопротивлением теплопередачи многослойной цилиндрической стенки и равна 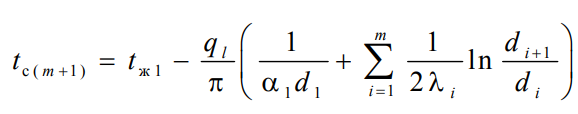 Температуры стенок Вопрос 7. Теплопроводность при наличии внутренних источников теплоты (однородная пластина) В П 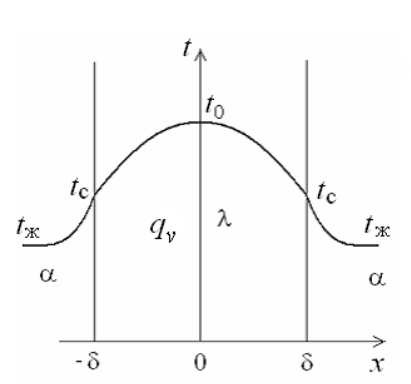 остоянные интегрирования определяются в зависимости от условий охлаждения на поверхности пластины. остоянные интегрирования определяются в зависимости от условий охлаждения на поверхности пластины. Рассмотрим длинную пластину, толщина которой 2 – величина малая по сравнению с двумя другими размерами Источники равномерно распределены по всему объему и равны qv = const. Заданы постоянные коэффициенты теплоотдачи = = const и температура жидкости вдали от пластины tж = const. Благодаря симметричному отводу теплоты температуры обеих поверхностей пластины одинаковы. При указанных условиях температура пластины будет изменяться только вдоль оси х, направленной нормально к поверхности тела Граничные условия на поверхностях пластины определяются из уравнения теплоотдачи П В перепад температур между осью симметрии стенки и ее поверхностью уравнение температурной кривой определяется выражением 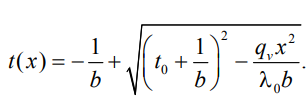 Вопрос 8. Теплопроводность при наличии внутренних источников теплоты (однородный цилиндрический стержень) Рассмотрим однородную цилиндрическую стенку (трубу) с внутренним диаметром d1 и наружным диаметром d2 с постоянным коэффициентом теплопроводности . Внутренние источники тепла qv = const равномерно распределены по объему тела. Заданы постоянные температуры подвижных сред tж1 и tж2, а также постоянные значения коэффициентов теплоотдачи 1 и 2 на внутренней и наружной поверхностях трубы. Необходимо найти распределение температуры в цилиндрической стенке, температуры ее поверхностей tс1 и tс2 и тепловой поток через нее 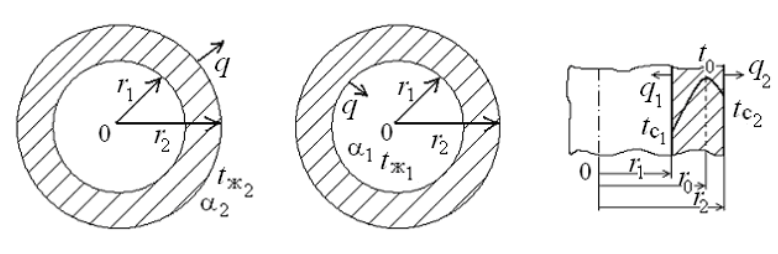 Е р 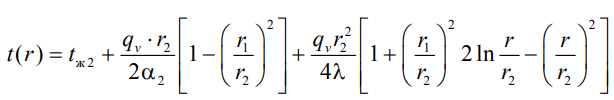 аспределение температуры в цилиндрической стенке аспределение температуры в цилиндрической стенке 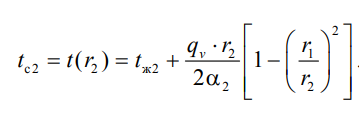 Температура наружной поверхности цилиндрической стенки Температура внутренней поверхности цилиндрической стенки У 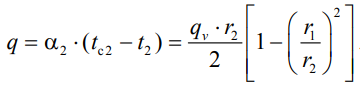 дельный тепловой поток с единицы теплоотдающей поверхности дельный тепловой поток с единицы теплоотдающей поверхности Е п 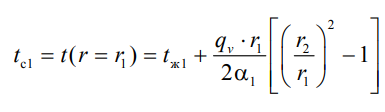 олучаем распределение температуры в цилиндрической стенке при отводе тепла только через внутреннюю поверхность олучаем распределение температуры в цилиндрической стенке при отводе тепла только через внутреннюю поверхность 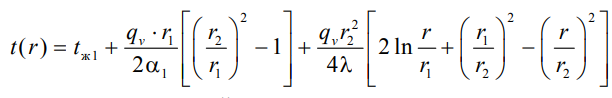 Температура внутренней поверхности Т 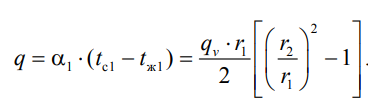 огда температура наружной поверхности будет определяться как огда температура наружной поверхности будет определяться как 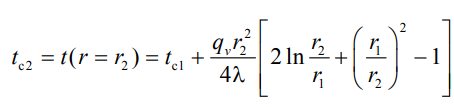 Удельный тепловой поток с единицы теплоотдающей поверхности В случае, если тепло отдается окружающей среде как с внутренней, так и с внешней поверхностей, должен существовать максимум температур внутри стенки. Изотермическая поверхность с r = r0, соответствующая максимальной температуре t0, разделяет цилиндрическую стенку на два слоя. Во внутреннем слое тепло передается внутрь трубы, во внешнем – наружу. Максимальное значение температуры соответствует условию dt/dr = 0 и, следовательно, q = 0. Таким образом, для решения данной задачи можно использовать уже полученные выше соотношения в которых следует заменить на r0 внутренний и наружный радиусы соответственно 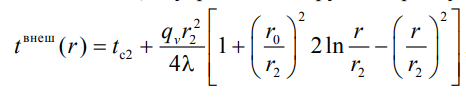 9. Теплопроводность при наличии внутренних источников теплоты (теплообмен в условиях электрического нагрева). теплообмен тел в условиях электрического нагрева Широкое использование электрического тока в процессах нагрева требует учета условий теплообмена для расчета электронагревателей. Теплота, которая выделяется во время прохождения электрического тока через нагреватель, расходуется на его нагрев, а также выделяется в окружающую среду. Если сила тока І, напряжение U, электрическое сопротивление проводника R, то количество теплоты, которое определяется по закону Джоуля-Ленца 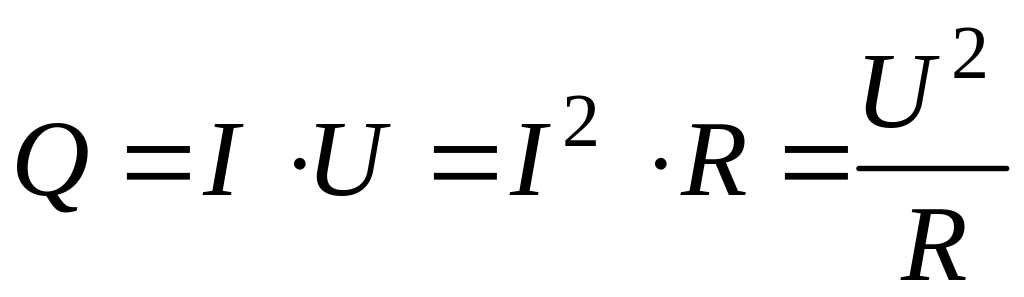 . .Для проводника с постоянным поперечным сечением электрическое сопротивление определяют 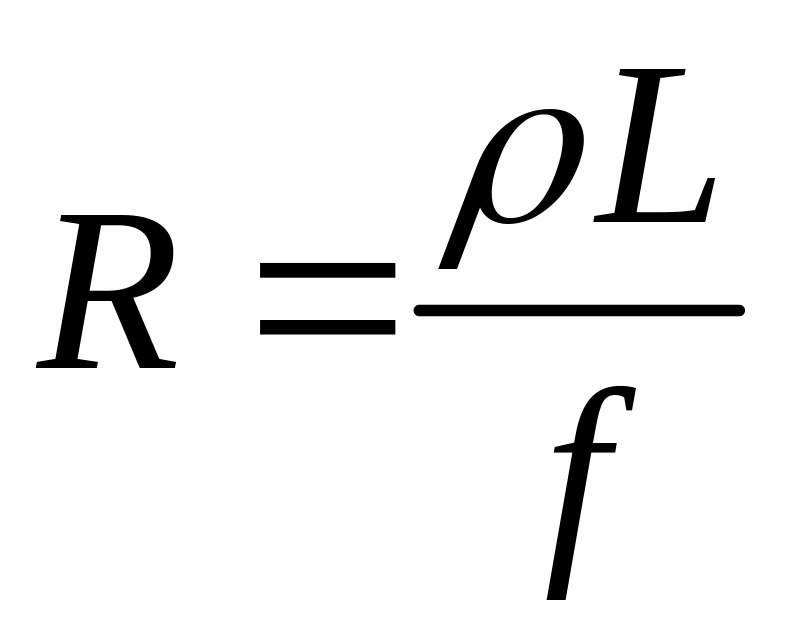 , ,где L – длина проводника, м; f – площадь поперечного сечения проводника, м2; С повышением температуры электрическое сопротивление тел увеличивается и его определяют где Количество теплоты, переданное нагревателем в окружающую среду при стационарном режиме, определяется где - коэффициент теплоотдачи, Вт/(м2К); F – поверхность проводника, м2; Тс и То.с. – температуры поверхности нагревателя и окружающей среды соответственно, К. В случае нагрева жидкости необходимо определить ее температуру. Принимая, что вся теплота, которую выделяет проводник, расходуется на нагрев жидкости, и что теплоемкость нагревателя очень мала по сравнению с теплоемкостью жидкости, которая нагревается, тепловой баланс системы за время где т1– масса жидкости, которая нагревается, кг; с1 – ее удельная теплоемкость, кДж/(кг∙К); Т1 – температура жидкости, которая нагревается, К; То.с. – температура окружающей среды, К; Время, необходимое для нагрева жидкости до температуры Т1, определяют 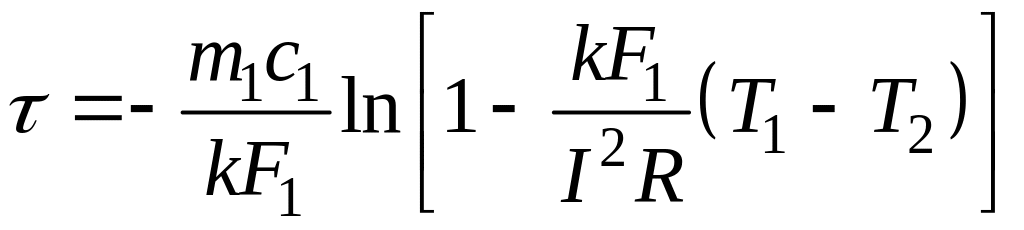 . .10)Нестационарная теплопроводность. Регулярный режим охлаждения (нагревания) тел. Темп охлаждения. Графический способ нахождения темпа охлаждения     11)Конвективный теплообмен в однородной среде. Основные понятия и определения (закон теплоотдачи Ньютона-Рихмана, коэффициент теплоотдачи, вынужденная и свободная конвекция). Понятие конвективного теплообмена охватывает процесс теплообмена при движении жидкости или газа. При этом перенос тепла осуществляется одновременно конвекцией и теплопроводностью. Конвекция тепла всегда сопровождается теплопроводностью, так как при движении жидкости или газа неизбежно соприкосновение отдельных частиц, имеющих различные температуры При практических расчетах используют закон Ньютона – Рихмана: Тогда для элемента поверхности dF Таким образом, коэффициент теплоотдачи есть плотность теплового потока на поверхности тела, отнесенная к разности температур между стенкой и жидкостью, и численно равен плотности теплового потока при температурном напоре, равном единице. Различают вынужденную и естественную конвекцию. В первом случае жидкость или газ движутся за счет внешних для данного процесса сил (насос, вентилятор, ветер), во втором случае – за счет разности плотностей нагретых и холодных частиц жидкости. 12) Физические свойства жидкости (коэффициент теплопроводности, удельная теплоемкость, плотность, коэффициент температуропроводности, динамический коэффициент вязкости, кинематический коэффициент вязкости, сжимаемость жидкости, тепловое расширение жидкости). Особенно большое влияние на теплоотдачу оказывают следующие физические параметры: коэффициент теплопроводности λ ,удельная теплоемкость ϲ, плотность ρ, коэффициент температуропроводности a и коэф-µ Кинематическая вязкость капельных жидкостей пропорциональна динамической вязкости, так как их плотность слабо зависит от температуры. Напротив, у газов кинематический коэффициент вязкости сильно растет, так как с ростом температуры падает их плотность. коэффициентом кинематической вязкости 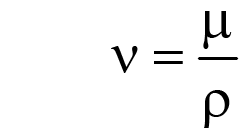 На теплоотдачу оказывает влияние сжимаемость жидкости. Изотермической сжимаемостью или коэффициентом сжатия тела при постоянной температуре называют положительную величину представляющую собой относительное изменение удельного объема при изменении давления на единицу 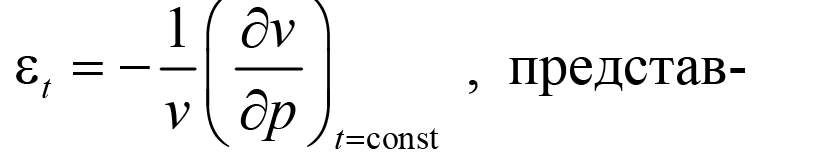 На конвективный теплообмен также оказывает влияние тепловое расширение жидкости, которое характеризуется температурным коэффициентом объемного расширения, определяемым уравнением. 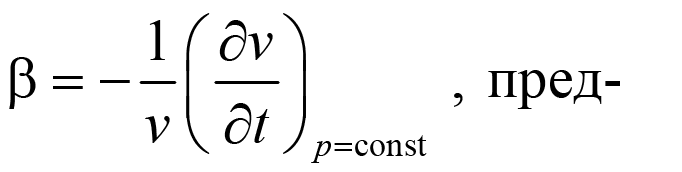 13) Теория подобия применительно к тепловым процессам. Числа теплового и гидромеханического подобия процессов (Nu, Re, Pr, Pe, Gr). Условия подобия физических процессов. Общие условия подобия физических процессов составляют содержание теоремы Кирпичева – Гухмана. 1. Подобные процессы должны быть качественно одинаковыми, т. е. они должны иметь одинаковую физическую природу и описываться одинаковыми по форме записи дифференциальными уравнениями. 2. Условия однозначности подобных процессов должны быть одинаковы во всем, кроме численных значений постоянных, содержащихся в этих условиях. 3. Одноименные определяющие критерии подобных процессов должны иметь одинаковую численную величину  14) Теплоотдача при вынужденном продольном омывании плоской поверхности.         1 2 |
