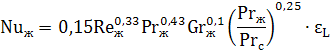Ответы на экзаменационные вопросы. вопросы экзамен тепломас обмен. Закон Фурье. Температурным полем называют совокупность мгновенных значений температуры во всех точках рассматриваемого пространства

Название	Закон Фурье. Температурным полем называют совокупность мгновенных значений температуры во всех точках рассматриваемого пространства
Анкор	Ответы на экзаменационные вопросы
Дата	01.04.2023
Размер	4.69 Mb.
Формат файла
Имя файла	вопросы экзамен тепломас обмен.docx
Тип	Закон #1029327
страница	2 из 2

1 2

теплопроводности, кинематической вязкости и температуропроводности, – которые, в свою очередь, являются функцией температуры .

15)Теплоотдача при вынужденном течении жидкости в трубах. Зависимость Nu от Re и Pr для турбулентного режима течения жидкости.
Теплоотдача при вынужденном течении жидкости в трубах и каналах

Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).

При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.

Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).

Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м²·град), который определяется по формуле:

Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, равный

F – площадь сечения канала, м²; П – периметр канала, м.

Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.

В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.

Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.

Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
Турбулентный режим течения в трубах наблюдается при числах Re более 10000.

Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).

Число Re определяется по формуле:

w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м²/с.

Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.

Теплоотдача при ламинарном течении в трубах и каналах

Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.

Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.

g – ускорение свободного падения, м/с²;

β – температурный коэффициент объемного расширения, град^-1;

d – эквивалентный диаметр канала, м;

ν — кинематическая вязкость жидкости при средней температуре, м²/с;

Δt – средняя разность температур жидкости и стенки, °С.

Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10⁵, то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:

Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.

Число Прандтля с индексом «с» Pr_с берется для жидкости при температуре стенки.

ε_L – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:

L/d	1	2	5	10	15	20	30	40	50
ε_L	1,9	1,7	1,44	1,28	1,18	1,13	1,05	1,02	1
Значения коэффициента ε_L при ламинарном режиме

Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr<8·10⁵, влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:

d – эквивалентный диаметр канала, м;

L – длина трубы (канала), м.

Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:

λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);

d – эквивалентный диаметр, м.

Теплоотдача в трубах и каналах при турбулентном режиме

Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:

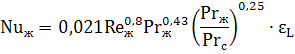
Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Pr_с берется при температуре стенки.

Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10⁴ до 5·10⁶ и Pr от 0,6 до 2500.

ε_L – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения ε_L приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:

Re_ж	L/d
Re_ж	1	2	5	10	15	20	30	40	50
1·10⁴	1,65	1,5	1,34	1,23	1,17	1,13	1,07	1,03	1
2·10⁴	1,51	1,4	1,27	1,18	1,13	1,1	1,05	1,02	1
5·10⁴	1,34	1,27	1,18	1,13	1,1	1,08	1,04	1,02	1
1·10⁵	1,28	1,22	1,15	1,1	1,08	1,06	1,03	1,02	1
1·10⁶	1,14	1,11	1,08	1,05	1,04	1,03	1,02	1,01	1
Значения коэффициента ε_L при турбулентном режиме

Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:

R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.

Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.

Расчет теплоотдачи при вынужденной конвекции

Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды t_ж=50°С, температура стенки трубы t_с=10°С.

1. Определим физические свойства воды при температуре 50°С:

Теплопроводность воды λ_ж= 0,648 Вт/(м·град);
Плотность воды ρ_ж=988 кг/м³;
Кинематическая вязкость воды ν_ж=0,556·10^-6, м²/с;
Число Прандтля при температуре жидкости Pr_ж=3,54;
Число Прандтля при температуре стенки Pr_с=9,52.

2. Рассчитаем среднюю скорость течения воды w по трубе:

3. Определим число Рейнольдса Re:

4. Поскольку число Рейнольдса имеет значение больше 1·10⁴, то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:

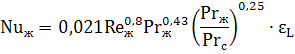
Определим коэффициент ε_L по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент ε_L=1_.

Выполним расчет числа Нуссельта по приведенному критериальному уравнению:

5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:

Выполним расчет:

Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м²·град).

16. Гидродинамический и тепловой пограничные слои при течении жидкости в круглой трубе. Участки гидродинамической и тепловой стабилизации

1 2