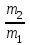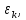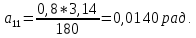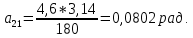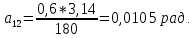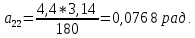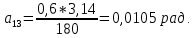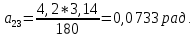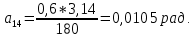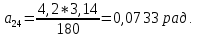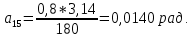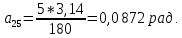лр 1-16. КЗИ-211.1 Богданович Милана_Ф_ЛР1-16.done. Определение коэффициента восстановления скорости при соударении шаров
 Скачать 274.44 Kb. Скачать 274.44 Kb.
|
|
Федеральное государственное бюджетное образовательное учреждение высшего образования «Омский государственный технический университет» Кафедра физики Отчёт по лабораторной работе № 1-16 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВОССТАНОВЛЕНИЯ СКОРОСТИ ПРИ СОУДАРЕНИИ ШАРОВ Выполнила: Студентка группы КЗИ-211 Богданович М.И. Проверил: Суриков В.И. Омск-2021 Лабораторная работа №1-16. Определение коэффициента восстановления скорости при соударении шаров. Краткая теория Ударом называется относительно кратковременное взаимодействие двух или более тел (время взаимодействия значительно меньше времени движения тел). Различают два предельных случая ударов: 1) абсолютно упругий удар, когда в процессе соударения между телами действуют силы упругости и после удара тела восстанавливают свою форму. 2) абсолютно неупругий удар, когда в процессе соударения тела необратимо деформируются и силы внутреннего трения, совершая работу, переводят механическую энергию тел частично или полностью в их внутреннюю энергию. После абсолютно неупругого удара тела движутся с одинаковыми скоростями (как одно целое) или покоятся. Исследуем некоторые вопросы, связанные с ударом двух тел на следующей лабораторной установке.   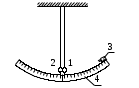 О 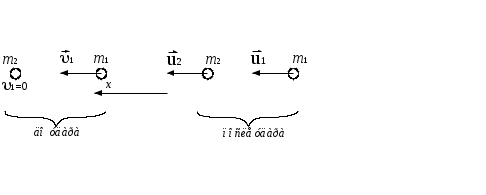 пыты по удару проводятся с помощью шаров, подвешенных на бифилярных подвесах, исключающих возможность их вращения. Отсчет отклонения шаров 1 и 2 от вертикали ведется по шкалам 4. Шар 1 можно удерживать в отклоненном положении с помощью электромагнита 3. пыты по удару проводятся с помощью шаров, подвешенных на бифилярных подвесах, исключающих возможность их вращения. Отсчет отклонения шаров 1 и 2 от вертикали ведется по шкалам 4. Шар 1 можно удерживать в отклоненном положении с помощью электромагнита 3.  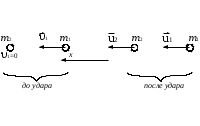 Рассмотрим процесс соударения. 1) Удар абсолютно упругий. В момент удара система, состоящая из двух шаров, не является замкнутой, так как на шары действуют внешние силы тяжести и реакции подвесов, причем их сумма не равна нулю, так как шары движутся по дуге окружности и обладают нормальным ускорением. В таком случае, как известно, закон сохранения импульса может быть записан для проекций импульсов тел на координатную ось, на которую внешние силы дают нулевые проекции. У нас в момент удара это горизонтальная ось Х. Тогда 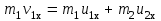 (1) (1)Так как силы, действующие на шары в момент удара, являются консервативными (силы тяжести и упругости), то полная механическая энергия системы до и после удара остается постоянной. Учтем при этом, что потенциальная энергия шаров до и после удара одинакова. Кроме того, в момент удара скорости шаров имеют отличную от нуля проекцию только на горизонтальную ось Х, поэтому при нахождении кинетических энергий можно заменить квадраты модулей скоростей квадратами проекций скоростей на ось Х Тогда 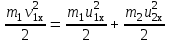 (2) (2)Решая совместно уравнения (1) и (2), легко найти 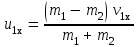 (3) (3)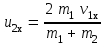 (4) (4) 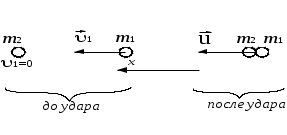 В уравнениях (3) и (4) знаки у проекций скоростей зависят от направления движения шаров до и после удара относительно оси Х. 2) Удар абсолютно неупругий. В данном случае система шаров также не является замкнутой и закон сохранения импульса следует записывать для проекций импульсов шаров на горизонтальную ось Х, на которую внешние силы тяжести и реакции подвеса дают нулевые проекции в момент удара. 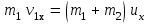 (5) (5)Отсюда получаем проекцию на ось Х общей скорости шаров после удара 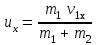 (6) (6)Закон сохранения механической энергии в данном случае не выполняется. В реальных опытах удар не бывает ни абсолютно упругим ни абсолютно неупругим. Величина, характеризующая упругие свойства материала тел при их соударении называется коэффициентом восстановления скорости и обозначается k. Он равен отношению модулей относительных скоростей тел после и до удара 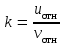 (7) (7)Значения величины k лежат в пределах от 0 (абсолютно неупругий удар) до 1 (абсолютно упругий удар). Из классического закона сложения скоростей следует, что в нашем случае 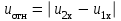 , , 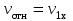 . .Тогда 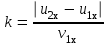 (8) (8) 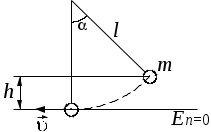 Непосредственное измерение скоростей шаров довольно сложно. Их можно вычислить, измеряя, например, углы отклонения подвесов шаров от вертикали до и после удара. На основании закона сохранения механической энергии можно приравнять полные энергии шаров в момент наибольшего отклонения (v = 0) и в нижней точке траектории (h = 0). При этом нулевой уровень потенциальной энергии проходит через положение равновесия шаров. 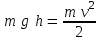 (9) (9)Высота подъема шара может быть найдена по углу его отклонения (см. рис.). 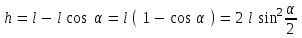 (10) (10)Подставляя (10) в (9), получим 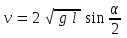 (11) (11)Учтем, что в нашем случае модули скоростей шаров до и после удара равны модулям их проекций на горизонтальную ось Х. Тогда 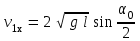 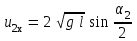 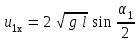  , ,где α0 – угол отклонения налетающего (первого) шара перед ударом, α2 – угол отклонения второго шара после удара, α1 – угол отклонения первого шара после удара. Подставим полученные выражения для проекций скоростей в формулу(8). После сокращений получим 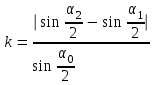 . .Известно, что для малых углов их синусы равны значениям самих углов в радианах. Если при проведении опытов использовать малые углы отклонения шаров (не более 10о), то в последнем выражении можно заменить синусы углов на значения углов, измеренные в радианах. Тогда для коэффициента восстановления k получим окончательную расчетную формулу 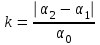 (12) (12)Экспериментальная часть В процессе выполнения работы необходимо задать массу маятника и пули. С помощью кнопок «огонь» и «зарядить» провести пять экспериментов с выбранными параметрами. Все результаты заносятся в таблицу. Таблица 1
Студентка гр. КЗИ-211 Богданович М.И. Дата выполнения 17.11.2021 Преподаватель Суриков В.И. Обработка результатов измерений Переведём значения углов aиз градусов в радианы по формуле: 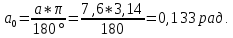
Найдём среднее значение углов отклонения первого и второго шара после удара: 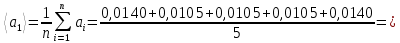 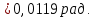 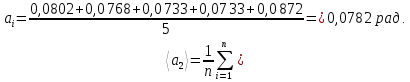 Найдём среднее значение коэффициента восстановления скорости: 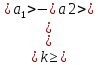 Произведём расчёты для a1 : Определим абсолютную погрешность величины 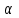 по правилам обработки результатов прямых измерений по правилам обработки результатов прямых измерений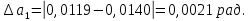 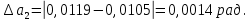 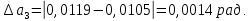 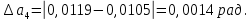 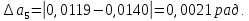 Рассчитаем среднеквадратическую погрешность 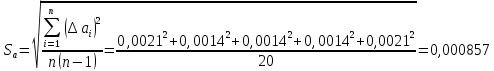 Задать величину надежности измерений а и по таблице найти значение коэффициента Стьюдента 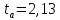 Найти случайную погрешность измерений 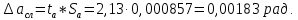 Найти приборную погрешность 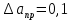 = 0,0017 рад. = 0,0017 рад.Вычислить абсолютную погрешность измерений 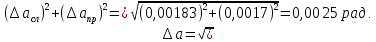 Вычислить значение относительной погрешности измерений 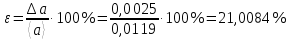 Записать результат обработки данных в виде: 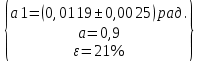 Произведём расчёты для a2: Определим абсолютную погрешность величины 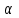 по правилам обработки результатов прямых измерений по правилам обработки результатов прямых измерений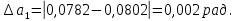 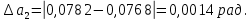 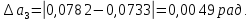 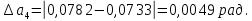 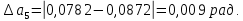 Рассчитаем среднеквадратическую погрешность 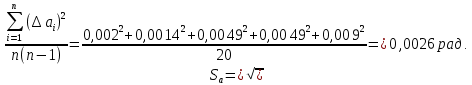 Задать величину надежности измерений а и по таблице найти значение коэффициента Стьюдента 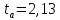 Найти случайную погрешность измерений 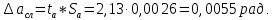 Найти приборную погрешность 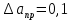 = 0,0017 рад. = 0,0017 рад.Вычислить абсолютную погрешность измерений 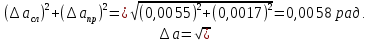 Вычислить значение относительной погрешности измерений 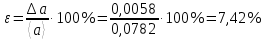 Записать результат обработки данных в виде: 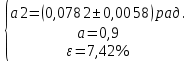 Найдём погрешность величины k по правилам обработки результатов косвенных воспроизводимых измерений: 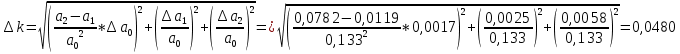 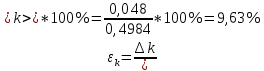 Выводы Изучен метод определение коэффициента восстановления скорости при соударении шаров, подвешенных на тонких параллельных нитях одинаковой длины, который равен отношению модулей относительных скоростей тел после и до удара В процессе выполнения работы были измерены угол отклонения второго шара после удара и угол отклонения первого шара после удара. Рассчитано экспериментальное значение коэффициента восстановления скорости при соударении шаров и погрешность коэффициента восстановления скорости: 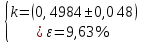 |