Линейные представления конечных групп( начало). Курсовая работа Заметки. Определение Моноид G, все элементы которого обратимы, называется группой. Другими словами, предполагаются выполненными следующие аксиомы.
 Скачать 21.78 Kb. Скачать 21.78 Kb.
|
|
Определение 1. Моноид G, все элементы которого обратимы, называется группой. Другими словами, предполагаются выполненными следующие аксиомы. 1) На множестве G определена бинарная операция (x, у) => ху. 2) Операция ассоциативна: (ху)z= x(уz) для всех x, у, z 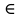 G. G.3) С обладает нейтральным (единичным) элементом е: хе = еx = х для всех x 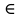 G. G.4) Для каждого элемента x 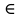 G существует обратный x⁻¹ : x x⁻¹= x⁻¹x=e. G существует обратный x⁻¹ : x x⁻¹= x⁻¹x=e.Несколько примеров групп: В полной линейной группе GLn (R) рассмотрим подмножество SLn(R) матриц с определителем 1: SLn(R) = {А 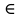 GLn (R) | det А = 1}. GLn (R) | det А = 1}.Очевидно, что Е 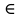 SLn(R) . SLn(R) . det A=1, det B=1 => det AB=1 det A⁻¹= (det A)⁻¹= 1 Поэтому SLn(R) — подгруппа в GLn (R); она носит название специальной линейной группы степени n над R. Её называют ещё и унимодулярной группой. Используя рациональные числа вместо вещественных, мы придём к полной линейной группе GLn (Q) степени n над Q и к её подгруппе SLn (Q). В свою очередь GLn (Q) содержит интересную подгруппу GLn (Z) Положив в примерах 1 и 2 n = 1, мы придём, во-первых, к мультипликативным группам R*=R\ {0} =G L1(R), Q* =Q\ {0} =G L1(Q) вещественных и рациональных чисел. Теорема 1. Число неприводимых попарно неэквивалентных представлений конечной группы G над C равно числу её классов сопряжённых элементов. Неприводимые представления Определение 2. Пусть р: G 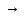 GL (V)- некоторое линейное представление группы G. Представление р называется неприводимым, если пространство V отлично от нуля и не имеет G-инвариантных подпространств, кроме 0 и V. Это эквивалентно утверждению, что V не разлагается в прямую сумму двух представлений. GL (V)- некоторое линейное представление группы G. Представление р называется неприводимым, если пространство V отлично от нуля и не имеет G-инвариантных подпространств, кроме 0 и V. Это эквивалентно утверждению, что V не разлагается в прямую сумму двух представлений.Определение 3.Пусть Р и Р'— два представления группы G; V и V' — соответствующие пространства представлений. Представления Р и Р' считаются эквивалентными, если существует изоморфизм J пространства V и V', такой, что Р' (s)( J)=J(Р (s)) для всех S 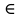 G; эквивалентность может иметь место только в том случае, если основные поля пространств V и V'совпадают. G; эквивалентность может иметь место только в том случае, если основные поля пространств V и V'совпадают. Определение 4. Конечная группа- алгебраическая группа, содержащая конечное число элементов (это число называется её порядком). Далее группа предполагается мультипликативной, то есть операция в ней обозначается как умножение; аддитивные группы с операцией сложения оговариваются особо. Единицу мультипликативной группы будем обозначать символом 1. Определение 5. Пусть G — произвольная (для определенности, мультипликативная) группа и а — один из ее элементов. Каждый элемент b вида g⁻'ag, гдеg 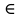 G, называется сопряженным с а. (Условимся писать в этом случае b G, называется сопряженным с а. (Условимся писать в этом случае b 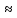 а.) Говорят еще, что элемент b получается трансформированием элемента а с помощью элемента g. а.) Говорят еще, что элемент b получается трансформированием элемента а с помощью элемента g.Отметим следующие свойства отношения сопряженности 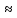 : : Каждый элемент сопряжен самому себе, а 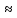 а (рефлексивность отношения а (рефлексивность отношения 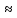 ),—так как а =e⁻¹ae. ),—так как а =e⁻¹ae.Если элемент b 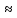 а, то а а, то а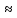 b (симметричность отношения b (симметричность отношения 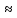 ) — так как из равенства b =g⁻¹ag вытекает, что а = gbg⁻¹=( g⁻¹)⁻¹bg⁻¹. ) — так как из равенства b =g⁻¹ag вытекает, что а = gbg⁻¹=( g⁻¹)⁻¹bg⁻¹.Если а 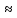 b и b b и b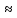 с; то a с; то a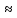 с (транзитивность отношения с (транзитивность отношения 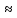 ). ). Таким образом, отношение сопряженности 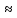 рефлексивно, симметрично и транзитивно, а значит, оно является отношением эквивалентности и определяет разбиение группы С на непересекающиеся классы сопряженных между собой элементов. рефлексивно, симметрично и транзитивно, а значит, оно является отношением эквивалентности и определяет разбиение группы С на непересекающиеся классы сопряженных между собой элементов. |
