НПК. НПК_Стусов_К_Павлинская_ВЭ. Умножение без таблицы
 Скачать 164.62 Kb. Скачать 164.62 Kb.
|
|
Государственное бюджетное образовательное учреждение республики Хакасия «Школа-интернат для детей с нарушениями зрения» «Умножение без таблицы» Выполнил: Стусов Кирилл ученик 5 а класса Руководитель: Павлинская В.Э. учитель математики г. Абакан 2022 Оглавление: Ведение……………………………………………………………………………….3 Способы умножения без таблицы умножения……………………………………..4 1. Русский способ умножения………………………………………………………4 2. Китайский способ умножения……………………………………………………5 3. Японский способ умножения…………………………………………………….7 Заключение…………………………………………………………………………...9 Список литературы…………………………………………………………………10 Ведение Умножение чисел — это казалось бы очень простая вычислительная операция, но вы не сможете выполнить умножение многозначных чисел, если не будете знать все результаты умножения однозначных чисел — таблицу умножения. В школе такую большую таблицу учат наизусть, а в дальнейшем — умножать числа в столбик. Но проблема в том, что эту таблицу хорошо знают далеко не все и поэтому возник вопрос: «А можно ли не учить ее вовсе и перемножать числа без таблицы умножения?» Так я выдвинул гипотезу: Существуют ли способы умножения без использования таблицы умножения? Объектом моего исследования стало само действие умножения, а предметом — различные способы умножения без таблицы умножения. Цель исследования: рассмотреть различные способы умножения без использования таблицы умножения и проверить их на практике. Задачи: 1. Изучить методическую литературу по теме исследования 2. Рассмотреть методы умножения при которых не нужно знать таблицу умножения и проверить на практике. 3. Развить навыки самостоятельной работы: поиск и отбор необходимой информации, оформление найденного материала. Для подтверждения актуальности нашей темы было проведено анкетирование учеников 5А и 5Б классов. Анализ результатов показал, что 36% обучающихся до сих пор ошибаются в результатах табличных произведений, четверть опрошенных выучили таблицу умножения за месяц, а вот всем остальным понадобилось не меньше полугода, при этом ни один из ребят не знает способов умножения чисел без таблицы умножения. Способы умножения без таблицы умножения За тысячелетия развития математики было придумано много способов умножения без таблицы умножения. Считалось, что для овладения искусством быстрого умножения нужно особое природное дарование. Простым людям, не обладающим особым математическим даром, это искусство недоступно. Например, в 15 веке итальянский математик Лука Пачоли приводит только 8 способов умножения, а в книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» (1914) изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще (способы), скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках». И все эти приемы умножения — «шахматный или органчиком», «загибанием», «по частям или в разрыв», «крестиком», «решеткой», «задом наперед», «ромбом», «треугольником», «кубком или чашей», «алмазом» и прочие соперничали друг с другом в громоздкости и сложности. Усваивались они с большим трудом и лишь после продолжительной практики. Рассмотрим некоторые, самые интересные на мой взгляд, из них. 1 Русский способ умножения Этот способ был в обиходе русских крестьян и унаследован ими с глубокой древности. Суть способа: умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом удваивают другое число. Последнее удвоенное число и есть искомый результат. Способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить, поэтому в результате многократного повторения этой операции получается искомое произведение. Пример 1: 16 х 32 = 512 16 | 32 8 | 64 4 | 128 2 | 256 1 | 512 Однако, если приходится делить пополам нечетное число, необходимо откинуть единицу и делим остаток пополам, при этом к последнему числу прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца — сумма будет искомых произведением. Пример 2: 17 х 37 = 37 + 592 = 629 17 | 37 8 | 74 4 | 148 2 | 296 1 | 592 Пример 3: 6 х 135 = 540 + 270 = 810 6 | 135 3 | 270 1 | 540 Очень простой и элегантный способ умножения. 2. Китайский способ умножения Данный способ умножения очень творческий, в виде замысловатых рисунков. Рассмотрим на примерах. Пример 1: 12 х 23 = 276  Рисуем первое число сверху вниз, второе число слева направо. Затем простым карандашом гуляя по рисунку и отмечаем все точки пересечения. Двигаясь справа налево собираем и считаем точки и получаем результат. Но и в этом способе есть ньюансы. Пример 2: 32 х 142 = 4544  Так же рисуем первое число сверху вниз, второе число слева направо. Затем так же гуляя по рисунку отмечаем точки пересечения. Двигаясь справа налево собираем и считаем точки. Первые точки посчитав получилось 4, это однозначное число, его оставляем. Вторая линейка складываем 6 точек и 8 точек, получаем 14 это двухзначное число. Оставляем число, записанное в разряде единиц — 4, число, находящиеся в разряде десятков, запоминаем — 1. Считаем следующую линейку: складываем 12 точек сверху, 2 снизу и 1, которую запомнили, получилось опять двухзначное число 15. Записываем число, записанное в разряде единиц — 5, а число из разряда десятков — 1, опять запоминаем. Считаем последнюю линейку: складываем 3 точки и 1, которую запомнили. Записываем результат. Данный способ подходит творческим людям. Он достаточно прост, но, конечно, занимает много места. 3. Японский способ умножения Данный способ умножения предполагает использование кругов и линий, чем-то похож на китайский. Рассмотрим на примере: Пример 1: 13 х 23 = 299 Первый множитель 13, значит один круг целый, а второй состоит из трех кругов наложенных друг на друга. Так как мы умножаем на двузначное число, то чертим два одинаковых столбца. 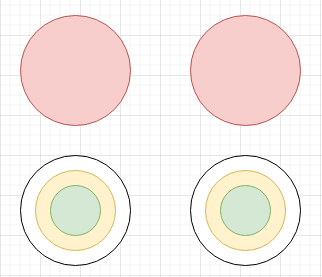 Второй множитель 23, поэтому круги в первом столбце делим на две части, а во втором — на три. 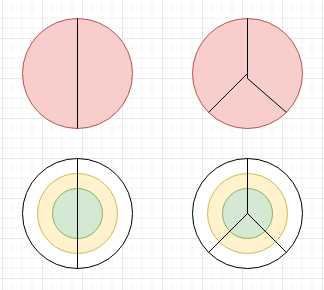 Затем проводим прямые и считаем точки как в китайском способе умножения. 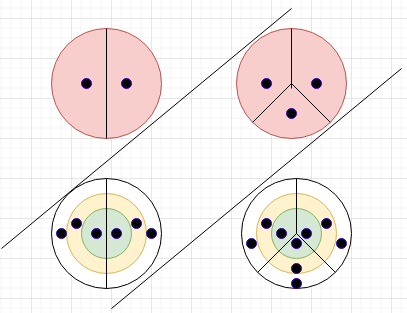 Справа налево: 9, далее по диагонали 6 точек в одном и 3 точки в другом круге — 9 точек, и 2 точки в последнем. Получаем 299. Если первый множитель трехзначное число, то строчек будет три, если второй множитель это трехзначное число, то столбцов будет три и так далее. Способ красочный, но так же посчитался мне громоздким. Заключение В истории математики есть много интересных событий и открытий, к сожалению не вся эта информация доходит до нас, современных учеников. В ходе роботы мы узнали о том, что раньше было не лёгким делом владеть этим действием, не существовало еще, как теперь, одного выработанного практикой приема. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения — приемы один другого запутаннее, твердо, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, восхвалял собственный способ выполнения этого действия. Признавалось даже, что для овладения искусством быстрого и безошибочного умножения многозначных чисел нужно особое природное дарование, исключительные способности; рядовым людям премудрость эта недоступна. Своей работой мы доказали, что наша гипотеза верна, действительно существует целое множество способов умножения не используя таблицу умножения: русский, китайский и японский. Несмотря на громоздкоть и необычность данные способы действительно работают, мы это проверили на примерах. А ещё мы научились подбирать материал, обрабатывать его, то есть выделять главное и систематизировать. Список литературы Буянов Е. Китайское и японское умножение, 2015. URL:https://4brain.ru/blog/китайское-или-японское-умножение/ (дата обращения: 4.02.2022г) Данилова А. История создания таблицы умножения. URL: https://www.timetoast.com/timelines/1000-3645448e-16f6-4a66-8908-e59cadf94cd7 (дата обращения: 21.12.21г) Депман И. Я., Виленкин Н. Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред.шк.-М.: Просвещение, 1989 Перельман Я. И. Занимательная арифметика. Издание:8, 1954 |
