лабораторная работа по информатике. лабораторная 1. Определение оптимального плана перевозок методом потенциалов

• Название: Определение оптимального плана перевозок методом потенциалов
• Анкор: лабораторная работа по информатике
• Дата: 20.05.2020
• Размер: 59.82 Kb.
• Имя файла: лабораторная 1.docx
• Тип: Отчет; #124123

Отчет о лабораторной работе № 1

по дисциплине: ИНФОРМАТИКА

на тему: Определение оптимального плана перевозок методом потенциалов.

Студент: : Тилилейкина Ирина Алксандовна

(фамилия, имя, отчество)

Группа: 17-ФАБ-СТ1

(шифр группы)

Вариант: 13( 3)

(номер варианта)

Преподаватель: к.т.н. Горовенко Л.А.

(фамилия, инициалы)

Цель работы: Изучить и применить на практике численные методы линейного программирования для задач транспортного типа.

Ход работы:

Задание : Три предприятия производят некоторую однородную продукцию в количествах, соответственно равных 50, 30 и 10 ед. Эту продукцию получают четыре потребителя в количествах, соответственно равных 30, 30 и 10 и 20 ед. Каждому потребителю продукция может завозиться с любого предприятия. Тарифы перевозок заданы матрицей. Требуется найти оптимальное решение доставки продукции от поставщиков к потребителям.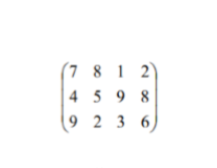


Решение:

	B1	B2	B3	B4	Запасы
A1	7	8	1	2	50
A2	4	5	9	8	30
A3	9	2	3	6	10
Потребности	30	30	10	20

Проверим необходимое и достаточное условие разрешимости задачи.
∑a = 50 + 30 + 10 = 90
∑b = 30 + 30 + 10 + 20 = 90
Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.
Поиск первого плана.
1. Используя метод наименьшей стоимости, построим первый опорный план
Искомый элемент равен c₁₃=1. Для этого элемента запасы равны 50, потребности 10. Поскольку минимальным является 10, то вычитаем его.
x₁₃ = min(50,10) = 10.
Искомый элемент равен c₁₄=2. Для этого элемента запасы равны 40, потребности 20. Поскольку минимальным является 20, то вычитаем его.
x₁₄ = min(40,20) = 20.
Искомый элемент равен c₃₂=2. Для этого элемента запасы равны 10, потребности 30. Поскольку минимальным является 10, то вычитаем его.
x₃₂ = min(10,30) = 10.
Искомый элемент равен c₂₁=4. Для этого элемента запасы равны 30, потребности 30. Поскольку минимальным является 30, то вычитаем его.
x₂₁ = min(30,30) = 30.
Искомый элемент равен c₁₂=8. Для этого элемента запасы равны 20, потребности 20. Поскольку минимальным является 20, то вычитаем его.
x₁₂ = min(20,20) = 20.


Далее, согласно алгоритму, ищем элементы среди не вычеркнутых.


Искомый элемент равен c₃₃=3, но т.к. ограничения выполнены, то x₃₃=0.

	B1	B2	B3	B4	Запасы
A1	7	8[20]	1[10]	2[20]	50
A2	4[30]	5	9	8	30
A3	9	2[10]	3[0]	6	10
Потребности	30	30	10	20

2. Значение целевой функции для этого опорного плана равно:
F(x) = 8*20 + 1*10 + 2*20 + 4*30 + 2*10 = 350
Улучшение опорного плана.
Проверим оптимальность опорного плана.

u₁ + v₂ = 8; 0 + v₂ = 8; v₂ = 8
u₃ + v₂ = 2; 8 + u₃ = 2; u₃ = -6
u₃ + v₃ = 3; -6 + v₃ = 3; v₃ = 9
u₁ + v₄ = 2; 0 + v₄ = 2; v₄ = 2
Для неизвестного потенциала u₂ нулевую поставку можно разместить в клетках:
(2;2), v₂=8
(2;3), v₃=9
(2;4), v₄=2
Для неизвестного потенциала v₁ нулевую поставку можно разместить в клетках:
(1;1), u₁=0
(3;1), u₃=-6
Среди этих клеток, в которых может быть размещена нулевая поставка, наименьший тариф имеет клетка (2, 2) с c₂₂ = 5. Следовательно, нулевую поставку размещаем в клетку (2, 2), и она становится условно занятой.
u₂ + v₂ = 5; -3 + v₂ = 5; v₂ = 8
Ранее поставленный псевдоноль из ячейки (3;3) убираем.
u₂ + v₁ = 4; -3 + v₁ = 4; v₁ = 7

	v1=7	v2=8	v3=9	v4=2
u1=0	7	8[20]	1[10]	2[20]
u2=-3	4[30]	5[0]	9	8
u3=-6	9	2[10]	3	6

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij
(1;3): 0 + 9 > 1; ∆₁₃ = 0 + 9 - 1 = 8 > 0
Выбираем максимальную оценку свободной клетки (1;3): 1
Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».


Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.
u₁ + v₂ = 8; 0 + v₂ = 8; v₂ = 8
u₂ + v₂ = 5; 8 + u₂ = 5; u₂ = -3
u₂ + v₁ = 4; -3 + v₁ = 4; v₁ = 7
u₃ + v₂ = 2; 8 + u₃ = 2; u₃ = -6
u₁ + v₃ = 1; 0 + v₃ = 1; v₃ = 1
u₁ + v₄ = 2; 0 + v₄ = 2; v₄ = 2

	v1=7	v2=8	v3=1	v4=2
u1=0	7	8[20]	1[10]	2[20]
u2=-3	4[30]	5[0]	9	8
u3=-6	9	2[10]	3	6

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.
Минимальные затраты составят: F(x) = 8*20 + 1*10 + 2*20 + 4*30 + 2*10 = 350
Из 1-го склада необходимо груз направить к 2-у потребителю (20), к 3-у потребителю (10), к 4-у потребителю (20)
Из 2-го склада необходимо весь груз направить к 1-у потребителю.
Из 3-го склада необходимо весь груз направить к 2-у потребителю.
Задача имеет множество оптимальных планов, поскольку оценка для (2;2) равна 0.

Выполнена _______________ подпись __________________

(число, месяц, год) (студента)

Проверил _______________ подпись __________________

(число, месяц, год) (преподавателя)