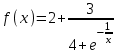ЛЕКЦИЯ 8. Определение предела функции в точке Предел функции на бесконечности. Односторонние пределы функции
 Скачать 174.25 Kb. Скачать 174.25 Kb.
|
|
ЛЕКЦИЯ 8. ПРЕДЕЛ ФУНКЦИИ. ОПРЕДЕЛЕНИЯ ПРЕДЕЛА ФУНКЦИИ План: Определение предела функции в точке Предел функции на бесконечности. Односторонние пределы функции Бесконечно большие функции 1. Определение предела функции в точке. Опр.4.4.1. Пусть а - предельная точка области определения Х функции f(x). Число b называется пределом функции при х, стремящемся к а, если для любого числа >0 существует такое число (вообще говоря, положительное и зависящее от ), что если хХ принадлежит также проколотой -окрестности 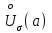 точки а, то значение функции f(x) принадлежит -окрестности числа b. точки а, то значение функции f(x) принадлежит -окрестности числа b. Обозначения: 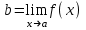 ; f(x)b при x а; ; f(x)b при x а; 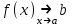 . .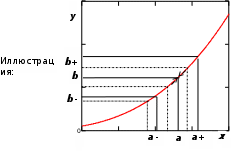 Краткая форма записи: Краткая форма записи: 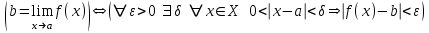 . .Неравенство 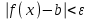 расписывается в виде двустороннего неравенства как расписывается в виде двустороннего неравенства как 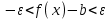 или или 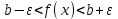 . Аналогично неравенство . Аналогично неравенство 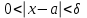 можно расписать как можно расписать как 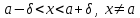 . Поэтому смысл определения предела таков: . Поэтому смысл определения предела таков: 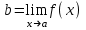 , если для любой наперед заданной степени близости значений f(x) к числу b мы в состоянии найти такую близость аргумента х к числу а, которая обеспечивает эту близость f(x) к b. Заметим, что в определении никак не участвует значение f(а) функции f(x) в точке а, в частности, f(а) не обязательно должно быть равным b; более того, f(x) может быть вообще не определена в точке а. , если для любой наперед заданной степени близости значений f(x) к числу b мы в состоянии найти такую близость аргумента х к числу а, которая обеспечивает эту близость f(x) к b. Заметим, что в определении никак не участвует значение f(а) функции f(x) в точке а, в частности, f(а) не обязательно должно быть равным b; более того, f(x) может быть вообще не определена в точке а.Рассмотрим два простых примера. Докажем, что 1. 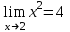 ; 2. ; 2. 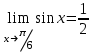 (дальше мы увидим, что предел любой элементарной функции при стремлении х к любой точке области определения этой функции равен значению функции в предельной точке). (дальше мы увидим, что предел любой элементарной функции при стремлении х к любой точке области определения этой функции равен значению функции в предельной точке).Возьмём >0. Требуется найти такое 0, что 0<| x-2 |<| x2-4 |<, т.е. | (x-2)(x+2) |<. Договоримся сразу брать <1, тогда из | x-2 |<2-<x<2+x<3x+2<5. Неравенство | (x-2)(x+2) |< будет обеспечено, если 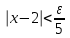 . Таким образом, если в качестве взять . Таким образом, если в качестве взять 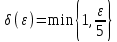 , то при | x-2 |<() получим |x+2|<5| (x-2)(x+2) |=| x-2 || x+2 |< , то при | x-2 |<() получим |x+2|<5| (x-2)(x+2) |=| x-2 || x+2 |<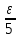 *5=, что и требовалось. *5=, что и требовалось. Возьмём >0. Требуется найти такое 0, что 0<| x-/6 |<| sin x-1/2 |< | sin x- sin(/6)|< 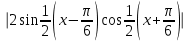 <.Так как <.Так как 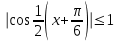 , |sin |<|| при 0, то требуемое неравенство будет выполнено, если взять ()= (Тогда из <| x-/6 |<= , |sin |<|| при 0, то требуемое неравенство будет выполнено, если взять ()= (Тогда из <| x-/6 |<= 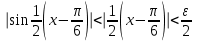 ; ; 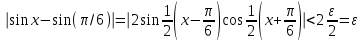 , что и требовалось. , что и требовалось.Более сложный пример-функция Дирихле В любой окрестности любого вещественного числа а имеются и рациональные, и иррациональные точки, обеспечить одновременное выполнение неравенств | b-1 |< и | b-0 |< при <1/2 невозможно ни при каком значении b, следовательно, функция Дирихле не имеет предела ни при каком стремлении аргумента. Рассмотрим ещё одно определение предела, эквивалентное предыдущему. Опр.4.4.2. Пусть {xn | xnX, xn a} - последовательность точек области определения функции f(x), сходящаяся к точке а. Если для любой такой последовательности {xn} последовательность значений функции {f(xn)} сходится к числу b, то b называется пределом f(x) при xа. (В МГТУ опр.3.4.1 принято называть определением Коши, опр.3.4.2 - определением Гейне). Докажем эквивалентность определений 4.4.1 и 4.4.2. Утв.1. Если 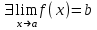 в смысле опр. 4.4.1, то число b - предел f(x) при xа и в смысле опр. 4.4.2. в смысле опр. 4.4.1, то число b - предел f(x) при xа и в смысле опр. 4.4.2.Док-во. Пусть {xn} сходится к а, требуется доказать, что {f(xn)} сходится к b, т.е. что для >0 N: n>N | f(xn)-b |< (в предположении, что выполняются условия опр. 4.4.1). Возьмём >0. : 0<| x-a |< | f(x)-b |<. Так как xnа при n , то N: n>N | xn-a |< |f(xn)-b |<. Нужное N найдено. Утв.2. Если 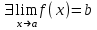 в смысле опр. 4.4.2, то число b - предел f(x) при xа и в смысле опр. 4.4.1. в смысле опр. 4.4.2, то число b - предел f(x) при xа и в смысле опр. 4.4.1.Док-во от противного. Мы предположим, что требования опр. 4.4.1 не выполняются, и построим последовательность {xn}, сходящуюся к а, для которой {f(xn)} не сходится к b. Если требования опр. 4.4.1 не выполняются, то >0, для которого в любой проколотой -окрестности точки а найдётся точка x, в которой | f(x)-b |>. Возьмём 1=1. x1а: 0<| x1-a |<1, но | f(x1)-b |>. Возьмём 2 |xn-1-a |}. xn: 0<| xn-a |<n, но |f(xn)-b |>, и т.д. Мы получили, что xnа при n (так как | xn-a |<1/n), но | f(xn)-b|>, т.е. {f(xn)} не сходится к b. Противоречие получено. Рассмотрим ещё два примера. 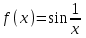 ( график этой функции приведен слева; х0). Докажем, что эта функция не имеет предела при х0. В каждой точке последовательности ( график этой функции приведен слева; х0). Докажем, что эта функция не имеет предела при х0. В каждой точке последовательности 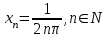 f(xn)=0, в к f(xn)=0, в к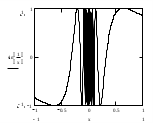 аждой точке последовательности аждой точке последовательности 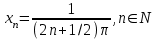 f(xn)=1, разные последовательности дают разные пределы f(xn)=1, разные последовательности дают разные пределы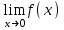 не существует. не существует.5. Функция Римана 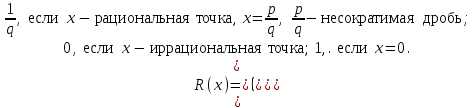 Как следует из графика, приведённого на стр.17, в любой -окрестности точки 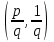 при < при <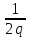 содержится не более чем конечное число значений функции, т.е. при рациональном значении аргумента х=а содержится не более чем конечное число значений функции, т.е. при рациональном значении аргумента х=а 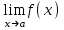 не существует. Если х=а иррационально, то вне любой -полосы |x|< лежит не более чем конечное число точек графика, т.е. не существует. Если х=а иррационально, то вне любой -полосы |x|< лежит не более чем конечное число точек графика, т.е. 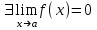 . .4.4.1.2. Предел функции на бесконечности. Опр.4.4.3. Пусть область определения Х функции f(x) неограничена. Число b называется пределом функции при х, стремящемся к , если для любого числа >0 существует такое число K, что если хХ удовлетворяет условию | x |>K, то значение функции f(x) принадлежит -окрестности числа b. Обозначения: 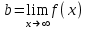 ; f(x)b при x ; ; f(x)b при x ; 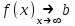 . . Краткая форма записи: Краткая форма записи: 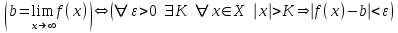 . . Пример: докажем, что 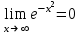 . . 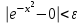 при при 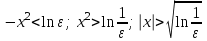 . Если взять K> . Если взять K>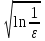 , то при | x |>K будет , то при | x |>K будет 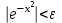 , что и требуется. , что и требуется.Задание. 1. Самостоятельно сформулировать определение 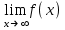 на языке последовательностей. 2.Сформулировать условие отсутствия на языке последовательностей. 2.Сформулировать условие отсутствия 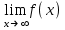 . .4.4.2. Односторонние пределы функции. Опр.4.4.4. Число b называется пределом функции f(x) при ха справа (или правым, правосторонним пределом), если для любого числа >0 существует такое число , что если хХ удовлетворяет неравенству a < x<а +, то | f(x)-b |<. Обозначения: 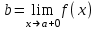 ; f(x)b при x а+0; ; f(x)b при x а+0; 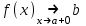 ; f(а+0). ; f(а+0).Опр.4.4.5. Число b называется пределом функции f(x) при ха слева (или левым, левосторонним пределом), если для любого числа >0 существует такое число , что если хХ удовлетворяет неравенству a- < x<а, то | f(x)-b |<. Обозначения: 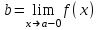 ; f(x)b при x а-0; ; f(x)b при x а-0; 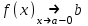 ; f(а-0). ; f(а-0).Односторонние пределы на бесконечности: Опр.4.4.6. Число b называется пределом функции f(x) при х+, если для любого числа >0 существует такое число K, что если хХ удовлетворяет неравенству x>K, то | f(x)-b |<. Обозначения: 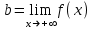 ; f(+). ; f(+).Опр.4.4.7. Число b называется пределом функции f(x) при х-, если для любого числа >0 существует такое число K, что если хХ удовлетворяет неравенству x<K, то | f(x)-b |<. Обозначения: 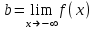 ; f(-). ; f(-).. Для примера рассмотрим функцию
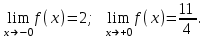 Найдем пределы этой функции при х. И при х-, и при х+ получим (-1/х) 0, е(-1/х)1, f(x) 2+3/5=13/5. Найдем пределы этой функции при х. И при х-, и при х+ получим (-1/х) 0, е(-1/х)1, f(x) 2+3/5=13/5. Связь между пределом функции и односторонними пределами устанавливает Теор. 4.4.1. Для того, чтобы существовал 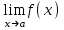 (или (или 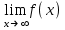 ), необходимо и достаточно, чтобы существовали и были равны односторонние пределы. ), необходимо и достаточно, чтобы существовали и были равны односторонние пределы.Док-во. Необходимость. Пусть 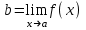 . Для 0 : 0<| x-a |< | f(x)-b |<. Но тогда | f(x)-b |< и при 0< x-a <(0< x<a +), и при -< x-a <0(a -< x<0), т.е. выполняются условия определений . Для 0 : 0<| x-a |< | f(x)-b |<. Но тогда | f(x)-b |< и при 0< x-a <(0< x<a +), и при -< x-a <0(a -< x<0), т.е. выполняются условия определений 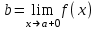 , , 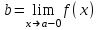 , следовательно, оба односторонние предела существуют и равны между собой. , следовательно, оба односторонние предела существуют и равны между собой.Достаточность. Пусть 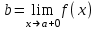 , , 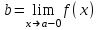 . Возьмём 0. Первый предел обеспечивает существование 1: a< x <a +1| f(x)-b |<. Аналогично второй предел обеспечивает существование 2: a -2< x<0| f(x)-b |<. Выберем . Возьмём 0. Первый предел обеспечивает существование 1: a< x <a +1| f(x)-b |<. Аналогично второй предел обеспечивает существование 2: a -2< x<0| f(x)-b |<. Выберем 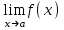 , и этот предел равен числу b. , и этот предел равен числу b. Задание 3. Самостоятельно сформулировать определение односторонних пределов на языке последовательностей. 4.Сформулировать условие отсутствия односторонних пределов. 4.4.3. Бесконечно большие функции. Опр.4.4.8. Функцияf(x) называется бесконечно большой при ха, если 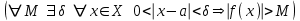 . .Обозначение: 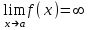 . .Опр.4.4.9. Функцияf(x) называется положительной бесконечно большой при ха, если 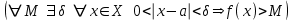 . .Опр.4.4.9. Функцияf(x) называется отрицательной бесконечно большой при ха, если 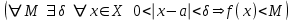 . .Такие же определения даются для случаев ха+0, ха-0, х+, х-. Пример: 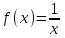 бесконечно большая при х0, положительная бесконечно большая при х+0, отрицательная бесконечно большая при х-0. Коротко эти свойства записываются с применением символики пределов так: бесконечно большая при х0, положительная бесконечно большая при х+0, отрицательная бесконечно большая при х-0. Коротко эти свойства записываются с применением символики пределов так: 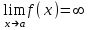 , , 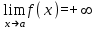 , , 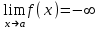 . Тем не менее, когда мы в дальнейшем будем говорить "пусть f(x) имеет предел при . Тем не менее, когда мы в дальнейшем будем говорить "пусть f(x) имеет предел при 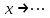 ", всегда будем предполагать, что этот предел конечен (противный случай будет специально подчёркиваться). ", всегда будем предполагать, что этот предел конечен (противный случай будет специально подчёркиваться). Если функция бесконечно большая, то она очевидно не ограничена. Но не всякая неограниченная функция - бесконечно большая. На графике справа изображена функция 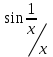 на отрезке [0.01, 0.1]. Эта функция неограничена на полуинтервале (0,1] (знаменатель 0), но в любой окрестности точки 0 имеются точки, в которых f(x)=0, т.е. f(x) не бесконечно большая. на отрезке [0.01, 0.1]. Эта функция неограничена на полуинтервале (0,1] (знаменатель 0), но в любой окрестности точки 0 имеются точки, в которых f(x)=0, т.е. f(x) не бесконечно большая.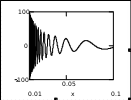 Для бесконечно больших функций будем применять аббревиатуру ББ. Для бесконечно больших функций будем применять аббревиатуру ББ.Задание. 6. Самостоятельно перебрать все возможные варианты определений ББ (положительных ББ, отрицательных ББ) при ха+0, ха-0, х+ и т.д. Сформулировать эти определения на языке последовательностей. |