РГР Норов. Определение ресурса долота при изменении технологических параметров
 Скачать 79.72 Kb. Скачать 79.72 Kb.
|
 МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ УНИВЕРСИТЕТ имени СЕРГО ОРДЖОНИКИДЗЕ» МГРИ КАФЕДРА СОВРЕМЕННЫХ ТЕХНОЛОГИЙ БУРЕНИЯ СКВАЖИН им. Воздвиженского Б. И. Расчетная работа Вариант 15 «Определение ресурса долота при изменении технологических параметров» Выполнил: ст. группы РТБ-18 Норов Ф. М. Проверила: преп. Сырчина А.С Москва, 2022 ОглавлениеЗадание 2 Определение основных статистических оценок выборки 3 Дисперсия и среднеквадратическое отклонение 4 Отбраковка по критерию Шовене 5 Правило «трех сигм» 5 Коэффициент вариации 5 Доверительный интервал. 6 Необходимое количество интервалов 6 Проверка закона распределения случайной величины. 7 Группировка данных. Построение гистограммы 8 Оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента 9 Оценка значимости различия средних значений двух выборок с использованием критерия Фишера 10 Вывод: 11 ЗаданиеЦель работы: научиться оценивать выборочную среднюю и выборочную дисперсию, определять доверительный интервал с заданной надежностью.
Задание: 1.Определение основных статистических оценок выборки: 1.1 Среднее арифметическое выборки. 1.2 Дисперсия. 1.3 Среднеквадратическое отклонение. 1.4 Отбраковка по критерию Шовене. 1.5 Правило «трех сигм». 1.6 Коэффициент вариации. 1.7 Доверительный интервал. 1.8 Необходимое количество экспериментов. 1.9 Проверка закона распределения случайной величины. 1.10 Группировка данных. Гистограмма. 2. Оценка значимости различия средних значений двух выборок 2.1Оценка значимости различия средних значений двух выборок с использованием критерия Стьюдента 2.2Оценка значимости различия средних значений двух выборок с использованием критерия Фишера Определение основных статистических оценок выборкиВыборочное среднее Выборочной средней называют среднее арифметическое значение признака выборочной совокупности Выборочное среднее x̅ выражается формулой: 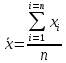 , где , где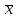 -среднее значение величины; -среднее значение величины;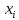 - значении случайной величины; - значении случайной величины;n-число испытаний. 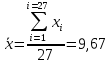 Дисперсия и среднеквадратическое отклонениеДисперсия случайных величин характеризует степень разброса вокруг ее среднего значения. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения. 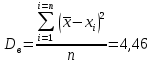 Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии: 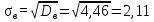 Исправленная дисперсия и среднее квадратическое отклонение Исправленная дисперсия является несмещенной оценкой генеральной дисперсии равна 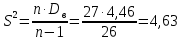 Исправленное среднее квадратическое отклонение равно 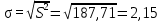 Отбраковка по критерию ШовенеПри проведении опытов при одинаковых условиях часто наблюдаются значения, резко отличающиеся от остальных. Отбраковка таких значений производится с помощью специальных методов. В работе мы использовали критерий Шовене. 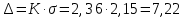 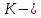 коэффициент Шовена, при коэффициент Шовена, при 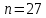 , ,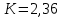 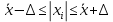 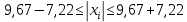 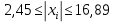 Все значения вошли в интервал Правило «трех сигм»Данное правило основано на том, что случайная величина при нормальном законе распределения практически полностью (на 99,7%) заключена в пределах 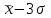 до до 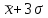 . Если значение случайной величины отличается от среднего значения . Если значение случайной величины отличается от среднего значения 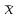 больше чем на 3 больше чем на 3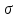 , то оно является аномальным. , то оно является аномальным.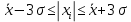 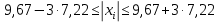 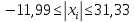 Все значения вошли в интервал Коэффициент вариацииНа практике широко применяют также характеристику рассеяния, называемую коэффициентом вариации, который представляет собой отношение среднего квадратичного отклонения к среднему значению. Коэффициент вариации показывает насколько велико рассеяние по сравнению со средним значением случайной величины. Коэффициент вариации выражается в долях единицы или в процентах. Вычисление коэффициента вариации имеет смысл для положительных случайных величин. 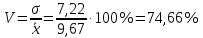 Доверительный интервал.Интервальная оценка с принятой вероятностью Р или уровнем значимости α определяет диапазон, в котором с определенной вероятностью будет находится истинное значение средней величины. 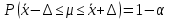 где Р- это доверительная вероятность, α- уровень значимости ∆= 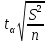 ∆-допустимое отклонение; 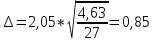 k=n-1, где k- степень свободы, 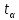 - критерий Стьюдента, для n=27 равен 2,05 - критерий Стьюдента, для n=27 равен 2,05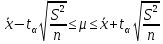 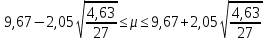 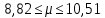 Необходимое количество интервалов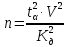 где Кд – коэффициент допустимого отклонения 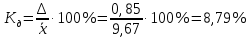 Тогда 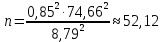 Проверка закона распределения случайной величины.Гипотеза о распределении показателя близком к нормальному, принимается если соблюдаются два условия: 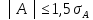 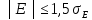 A 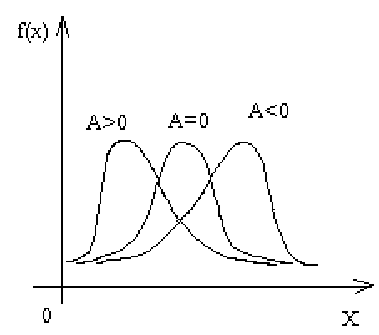 — показатель асимметрии (характеризует различия в крутизне склонов графика эмпирической дифференциальной функции распределения.) — показатель асимметрии (характеризует различия в крутизне склонов графика эмпирической дифференциальной функции распределения.) 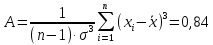 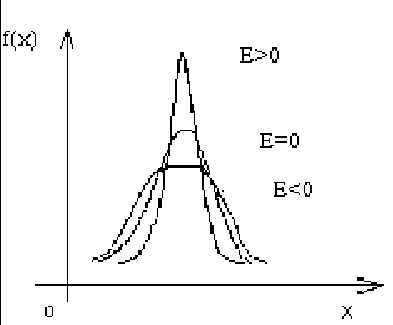 Е — показатель эксцесса (характеризует различия в крутизне вершины графика эмпирической дифференциальной функции распределения 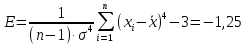 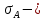 среднеквадратичное отклонение асимметрии нормального закона. среднеквадратичное отклонение асимметрии нормального закона.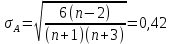 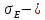 среднеквадратичное отклонение эксцесса нормального распределения. среднеквадратичное отклонение эксцесса нормального распределения.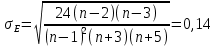 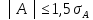 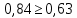 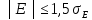 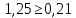 Оба условия не выполняются, следовательно выборка не подчиняется нормальному закону распределения. Группировка данных. Построение гистограммыЗначения случайных величин разбиваются на интервалы. Число интервалов определяется по формуле Стерджесса: 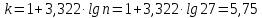 Определяем шаг интервала: 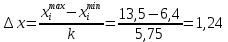 Найдем относительные частоты, плотность относительных частот и накопленные относительные частоты.
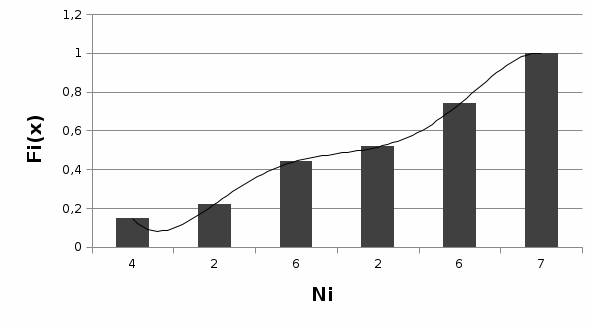 Рисунок 1 Гистограмма плотности относительных частот Оценка значимости различия средних значений двух выборок с использованием критерия СтьюдентаПри обработке результатов наблюдений часто возникает необходимость в проверке гипотез относительно средних значений 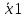 и и 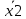 двух независимых выборок n1 и n2. При этом применяется выборочная статистика. двух независимых выборок n1 и n2. При этом применяется выборочная статистика.
Вычисляем средние значения выборок: 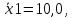 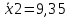 Вычисляем дисперсии выборок: 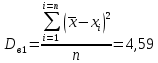 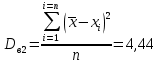 Когда обе дисперсии неизвестны и не предполагается, что они равны, т. е. 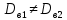 , равенство двух средних проверяют с помощью приближенного экспериментального коэффициента Стьюдента , равенство двух средних проверяют с помощью приближенного экспериментального коэффициента Стьюдента 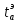 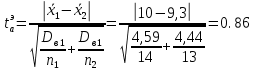 Табличное значение критерия Стьюдента при при а=0,5 и f=14+13=27 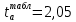 Так как 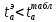 , то различие средних значений существенно, а значит, выборки не относятся к одной генеральной совокупности. , то различие средних значений существенно, а значит, выборки не относятся к одной генеральной совокупности.Оценка значимости различия средних значений двух выборок с использованием критерия ФишераРаспределение Фишера, называемое также Ф-распределением, используется для проверки гипотезы о равенстве дисперсий случайных величин. В качестве критерия Фишера 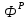 служит отношение дисперсий: служит отношение дисперсий: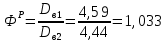 в числитель отношения всегда помещают большую дисперсию. Вычисленное значение критерия сравнивается с табличным значением 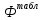 табличное значение критерия Фишера при 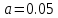 и и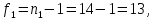 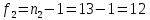 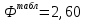 Так как 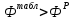 , то расхождение дисперсий велико и различие средних значений существенно. , то расхождение дисперсий велико и различие средних значений существенно.Вычисляем средневзвешенную дисперсию 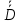 : :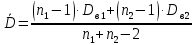 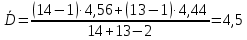 Табличное значение критерия Стьюдента при при 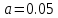 и и 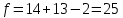 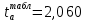 Выполняем проверку условия: 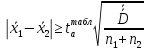 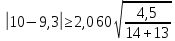 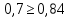 Так как условие не выполняется, то различие средних несущественно. Вывод:В данной работе определил основные статистические оценки выборки . Произвел отбраковку по методу Шовене, тем самым отбраковав элементы не вошедшие в интервал .Далее сделал тоже самое по методу трех сигм. После того как я избавился от аномальных значений выборки, для наглядной оценки, построил гистограмму. С помощью методов, используемых в данной работе, можно легко оценить адекватность значений выборки и проанализировать их. Была произведена оценка значимости различия средних величин двух выборок с помощью критерия Стьюдента и критерия Фишера. Было определено, что расхождение дисперсий велико и различие средних значений существенно. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
