Формулы для Ларисы. Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы
 Скачать 166.08 Kb. Скачать 166.08 Kb.
|
Определение случайного процесса. Основные подходы к заданию случайных процессов. Понятие реализации и сечения. Элементарные случайные процессы.Случайным (стохастическим, вероятностным) процессом называется функция действительного переменного t, значениями которой являются соответствующие случайные величины X(t). В теории случайных процессов t трактуется как время, принимающее значения из некоторого подмножества Т множества действительных чисел (t 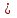 T, T T, T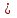 R). R).В рамках классического математического анализа под функцией y=f(t) понимается такой тип зависимости переменных величин t и y, когда конкретному числовому значению аргумента t соответствует и притом единственное числовое значение функции y. Для случайных процессов ситуация принципиально иная: задание конкретного аргумента t приводит к появлению случайной величины X(t) с известным законом распределения (если это дискретная случайная величина) или с заданной плотностью распределения (если это непрерывная случайная величина). Другими словами, исследуемая характеристика в каждый момент времени носит случайный характер с неслучайным распределением. Значения, которые принимает обычная функция y=f(t) в каждый момент времени, полностью определяет структуру и свойства этой функции. Для случайных процессов дело обстоит иным образом: здесь совершенно не достаточно знать распределение случайной величины X(t) при каждом значении t, необходима информация об ожидаемых изменениях и их вероятностях, то есть информация о степени зависимости предстоящего значения случайного процесса от его предыстории. Наиболее общий подход в описании случайных процессов состоит в задании всех его многомерных распределений, когда определена вероятность одновременного выполнения следующих событий: 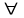 t1, t2,…,tn t1, t2,…,tn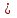 T, n T, n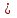 N: X(ti)≤xi; i=1,2,…,n; N: X(ti)≤xi; i=1,2,…,n;F(t1;t2;…;tn;x1;x2;…;xn)=P(X(t1)≤x1; X(t2)≤x2;…; X(tn)≤xn). Такой способ описания случайных процессов универсален, но весьма громоздок. Для получения существенных результатов выделяют наиболее важные частные случаи, допускающие применение более совершенного аналитического аппарата. В частности, удобно рассматривать случайный процесс X(t, ω) как функцию двух переменных: t 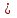 T, ω T, ω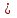 Ω, которая при любом фиксированном значении t Ω, которая при любом фиксированном значении t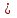 T становится случайной величиной, определенной на вероятностном пространстве (Ω, A, P), где Ω - непустое множество элементарных событий ω; A - σ-алгебра подмножеств множества Ω, то есть множество событий; P - вероятностная мера, определенная на A. T становится случайной величиной, определенной на вероятностном пространстве (Ω, A, P), где Ω - непустое множество элементарных событий ω; A - σ-алгебра подмножеств множества Ω, то есть множество событий; P - вероятностная мера, определенная на A.Неслучайная числовая функция x(t)=X(t, ω0) называется реализацией (траекторией) случайного процесса X(t, ω). Сечением случайного процесса X(t, ω) называется случайная величина, которая соответствует значению t=t0. Если аргумент t принимает все действительные значения или все значения из некоторого интервала T действительной оси, то говорят о случайном процессе с непрерывным временем. Если t принимает только фиксированные значения, то говорят о случайном процессе с дискретным временем. Если сечение случайного процесса - дискретная случайная величина, то такой процесс называется процессом с дискретными состояниями. Если же любое сечение - непрерывная случайная величина, то случайный процесс называется процессом с непрерывными состояниями. В общем случае задать случайный процесс аналитически невозможно. Исключение составляют так называемые элементарные случайные процессы, вид которых известен, а случайные величины входят как параметры: X(t)=Х(t,A1,…,An), где Ai, i=1,…,n - произвольные случайные величины с конкретным распределением. Некоторые классы и виды случайных процессов1.1.1. Гауссовские случайные процессы Случайный процесс X(t) называется гауссовским, если все его конечномерные распределения являются нормальными, то есть 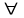 t1, t2,…,tn t1, t2,…,tn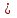 T Tслучайный вектор (X(t1); X(t2);…; X(tn)) имеет следующую плотность распределения: 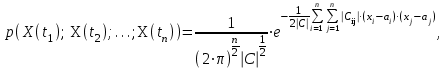 , ,где ai=MX(ti);  =M(X(ti)-ai)2; сij= M((X(ti)-ai)(X(tj)-aj)); =M(X(ti)-ai)2; сij= M((X(ti)-ai)(X(tj)-aj)); 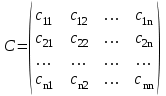 ; ;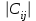 -алгебраическое дополнение элемента сij. -алгебраическое дополнение элемента сij.1.1.2. Случайные процессы с независимыми приращениями Случайный процесс X(t) называется процессом с независимыми приращениями, если его приращения на непересекающихся временных промежутках не зависят друг от друга: 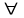 t1, t2,…,tn t1, t2,…,tn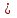 T: t1 ≤t2 ≤…≤tn, T: t1 ≤t2 ≤…≤tn, случайные величины X(t2)-X(t1); X(t3)-X(t2); …; X(tn)-X(tn-1) независимы. 1.1.3. Случайные процессы с некоррелированными приращениями Случайный процесс X(t) называется процессом с некоррелированными приращениями, если выполняются следующие условия: 1) 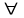 t t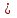 T: МX2(t) < ∞; T: МX2(t) < ∞;2) 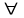 t1, t2, t3, t4 t1, t2, t3, t4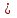 T: t1 ≤t2 ≤ t3≤ t4 : М((X(t2)-X(t1))(X(t4)-X(t3)))=0. T: t1 ≤t2 ≤ t3≤ t4 : М((X(t2)-X(t1))(X(t4)-X(t3)))=0.1.1.4. Стационарные случайные процессы (см. Глава 5) 1.1.5. Марковские случайные процессы Ограничимся определением марковского случайного процесса с дискретными состояниями и дискретным временем (цепь Маркова). Пусть система А может находиться в одном из несовместных состояний А1; А2;…;Аn, и при этом вероятность Рij(s) того, что в s-ом испытании система переходит из состояния 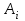 в состояние Аj, не зависит от состояния системы в испытаниях, предшествующих s-1-ому. Случайный процесс данного типа называется цепью Маркова. в состояние Аj, не зависит от состояния системы в испытаниях, предшествующих s-1-ому. Случайный процесс данного типа называется цепью Маркова.1.1.6. Пуассоновские случайные процессы Случайный процесс X(t) называется пуассоновским процессом с параметром а (а>0), если он обладает следующими свойствами: 1) t 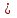 T; Т=[0, +∞); T; Т=[0, +∞);2) X(0)=0; 3) 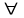 t1, t2, …,tn: 0≤t1 t1, t2, …,tn: 0≤t1 X(t2)-X(t1); X(t3)-X(t2); …; X(tn)-X(tn-1) независимы; 4) случайная величина X(t)-X(s), 0≤s≤t имеет распределение Пуассона с параметром а(t-s): 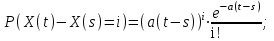 i=0;1;2;… i=0;1;2;… 1.1.7. Винеровский случайный процесс Случайный процесс X(t) называется винеровским, если он обладает свойствами: 1)-3) пуассоновского случайного процесса; 4) cлучайная величина X(t)-X(s), 0≤s≤t имеет нормальное распреде- ление с параметрами (0; 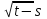 ): ):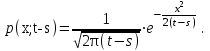 Понятие корреляционной теории случайных процессовВ рамках общего подхода к описанию случайных процессов характеристика сечений и любых их совокупностей осуществляется с помощью многомерных распределений. В частности, любое сечение характеризуется либо одномерной плотностью вероятности p1(t; х), либо одномерной функцией распределения F(t; х)=P(X(t)≤x). Взаимосвязь любой пары сечений характеризуется двумерной плотностью вероятности p2(t1; t2; х1; х2) или двумерной функцией распределения F(t1; t2; х1; х2)=P(X(t1)≤x1; X(t2)≤x2), где t1,2-два фиксированных момента времени; х1,2- возможные значения случайных величин, соответствующих этим сечениям. Аналогично вводятся плотности и функции распределения трех и более сечений, однако для большого числа случайных процессов оказывается достаточным ограничиться одномерными и двумерными распределениями. Теория случайных процессов, основанная на изучении моментов первого и второго порядка, называется корреляционной теорией случайных процессов. Математическое ожидание и дисперсия случайного процесса. Среднеквадратическое отклонениеЕсли в каждом сечении случайного процесса существует математическое ожидание, то математическим ожиданием случайного процесса X(t) называется неслучайная функция mX(t), значение которой при каждом фиксированном значении t равно математическому ожиданию соответствующего сечения: mX(t)=MX(t). Основные свойства математического ожидания случайного процесса: если φ(t) - неслучайная функция, то М φ(t)=φ(t); М(φ(t)X(t))=φ(t)mX(t); M(X1(t)+X2(t))= 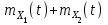 ; M(X(t)+φ( t))= mX(t)+ φ(t). ; M(X(t)+φ( t))= mX(t)+ φ(t).Если в каждом сечении случайного процесса существует дисперсия, то дисперсией случайного процесса X(t) называется неслучайная функция DХ(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии соответствующего сечения: DX(t)= DХ(t)= M(X(t)-mX( t))2. Основные свойства дисперсии случайного процесса: если φ(t) - неслучайная функция, то D(φ(t))=0; D(φ(t)X(t))=φ2(t)DX(t); D(X(t)+φ(t))=DX(t); 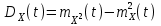 . .Среднеквадратическим отклонением случайного процесса X(t) называется арифметический квадратный корень из его дисперсии: 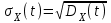 . .Корреляционная функция случайного процесса и ее свойства. Нормированная корреляционная функцияКорреляционной функцией случайного процесса X(t) называется неслучайная функция KX(t1; t2) двух независимых аргументов, значение которой равно корреляционному моменту сечений, соответствующих моментам времени t1 и t2: KX(t1; t2)=M((X(t1)-mX(t1))(X(t2)-mX(t2))). Основные свойства корреляционной функции: 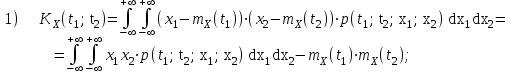 2) KX(t; t)=DX(t); 3) KX(t1; t2)= KX(t2; t1); 4) если φ(t) - неслучайная функция, то Kφ(t)(t1; t2)=0; Kφ(t)+X(t)(t1; t2)= KX(t)(t1; t2); Kφ(t)X(t)(t1; t2)= φ(t1) φ(t2)KX(t)(t1; t2); 5) 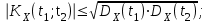 6) 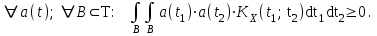 Функция вида 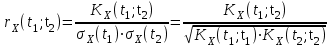 называется нормированной корреляционной функцией. называется нормированной корреляционной функцией.Взаимная корреляционная функция и нормированная взаимная корреляционная функция двух случайных процессовВзаимной корреляционной функцией двух случайных процессов X(t) и Y(t) называют неслучайную функцию RXY(t1; t2) двух независимых аргументов t1 и t2, значение которой равно корреляционному моменту сечений этих случайных процессов в соответствующие моменты времени: RXY(t1; t2)= M((X(t1)-mX(t1))(Y(t2)-mY(t2))). Свойства взаимной корреляционной функции: если φ(t) и Ψ(t) - неслучайные функции, то RX(t)+φ(t) Y(t)+Ψ(t)(t1; t2)= RXY(t1; t2); RX(t)φ(t) Y(t)Ψ(t)(t1; t2)= φ(t1) Ψ(t2)RXY(t1; t2); RXY(t1; t2)=RYX(t2; t1); 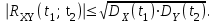 Функция вида 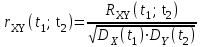 называется нормированной взаимной корреляционной функцией случайных процессов X(t) и Y(t). называется нормированной взаимной корреляционной функцией случайных процессов X(t) и Y(t).Вероятностные характеристики суммы двух случайных величинТеорема 1. Математическое ожидание суммы двух случайных процессов X(t) и Y(t) равно сумме их математических ожиданий: mX+Y(t)= mX(t)+mY(t). Теорема 2. Корреляционная функция суммы двух случайных процессов X(t) и Y(t) имеет вид: KX+Y(t1; t2)=KX(t1; t2)+KY(t1; t2)+RXY(t1; t2)+RYX(t2; t1). Следствие 1. Если случайные процессы X(t) и Y(t) некоррелированны, то KX+Y(t1; t2)=KX(t1; t2)+KY(t1; t2); DX+Y(t)=DX(t)+DY(t). Следствие 2. Если случайный процесс X(t) и случайная величина Y некоррелированны, то KX+Y(t1; t2)=KX(t1; t2)+DY. Производная случайного процесса и ее свойстваВ соответствии с классическим определением, производная случайного процесса X(t) должна быть определена как предел разностного отношения 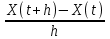 при h→0 в смысле соответствующей сходимости. Можно показать, что сходимость по вероятности обладает рядом недостатков, которые делают этот подход практически бесполезным. при h→0 в смысле соответствующей сходимости. Можно показать, что сходимость по вероятности обладает рядом недостатков, которые делают этот подход практически бесполезным.Случайный процесс X(t) называется дифференцируемым, если существует случайный процесс 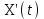 такой, что такой, что 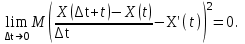 При этом случайный процесс 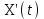 называется производной случайного процесса X(t) и обозначается следующим образом: называется производной случайного процесса X(t) и обозначается следующим образом: 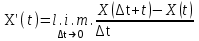 . .Теорема 1. Математическое ожидание производной случайного процесса равно производной от математического ожидания самого случайного процесса: 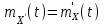 . .Следствие.  . .Теорема 2. Корреляционная функция производной случайного процесса X(t) равна второй смешанной производной от его корреляционной функции: 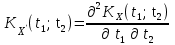 . .Теорема 3. Взаимная корреляционная функция случайного процесса X(t) и его производной 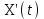 равна частной производной его корреляционной функции по переменной, соответствующей производной: равна частной производной его корреляционной функции по переменной, соответствующей производной: 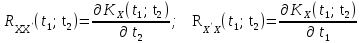 . .3.3. Интеграл от случайного процесса и его свойстваИнтегралом от случайного процесса X(t) на отрезке [0, t] называется предел в среднеквадратичном при λ→0 (n→0) 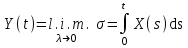 интегральных сумм 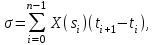 где si где si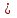 (ti; ti+1); λ=max(ti+1 - ti), i=0,…,n-1. (ti; ti+1); λ=max(ti+1 - ti), i=0,…,n-1.Теорема 4. Математическое ожидание интеграла от случайного процесса равно интегралу от его математического ожидания: 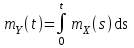 , , 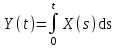 . .Теорема 5. Корреляционная функция интеграла от случайного процесса X(t) равна двойному интегралу от его корреляционной функции: 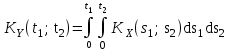 . .Теорема 6. Взаимная корреляционная функция случайного процесса X(t) и его интеграла равна интегралу от корреляционной функции случайного процесса X(t): 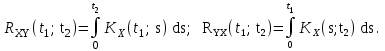 Канонические разложения случайных процессовПонятие канонического разложения случайного процессаСлучайная величина V называется центрированной, если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величины V на неслучайную функцию φ(t): X(t)=V φ(t). Элементарный центрированный случайный процесс имеет следующие характеристики: 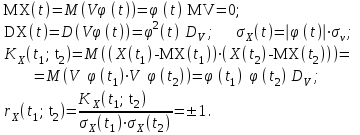 Выражение вида 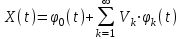 , где φk(t), k=1;2;…-неслучайные функции; , где φk(t), k=1;2;…-неслучайные функции;  , k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины , k=1;2;…-некоррелированные центрированные случайные величины, называется каноническим разложением случайного процесса X(t), при этом случайные величины  называются коэффициентами канонического разложения; а неслучайные функции φk(t) - координатными функциями канонического разложения. называются коэффициентами канонического разложения; а неслучайные функции φk(t) - координатными функциями канонического разложения.Рассмотрим характеристики случайного процесса 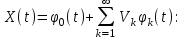 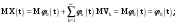 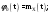 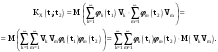 Так как по условию 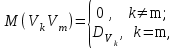 то то 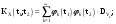 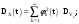 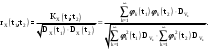 Очевидно, что один и тот же случайный процесс имеет различные виды канонического разложения в зависимости от выбора координатных функций. Более того, даже при состоявшемся выборе координатных функций существует произвол в распределении случайных величин Vк. На практике по итогам экспериментов получают оценки для математического ожидания и корреляционной функции: 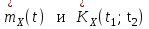 . После разложения . После разложения 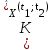 в двойной ряд Фурье по координатным функциям φк(t): в двойной ряд Фурье по координатным функциям φк(t): 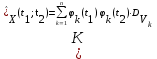 получают значения дисперсий 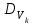 случайных величин Vk. случайных величин Vk.Понятие стационарного случайного процесса. Стационарность в узком и широком смыслахСтационарным (однородным во времени) называют случайный процесс, статистические характеристики которого не меняются с течением времени, то есть являются инвариантными относительно временных сдвигов. Различают случайные процессы стационарные в широком и узком смысле. Стационарным случайным процессом в узком смысле называется случайный процесс Х(t), все вероятностные характеристики которого не меняются со временем, то есть 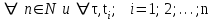 таких, что таких, что 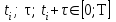 выполняется условие выполняется условиеF(t1; t2;… ;tn; x1; x2;…; xn)=F(t1+τ; t2+τ;… ;tn+τ; x1; x2;…; xn), и, следовательно, все n-мерные распределения зависят не от моментов времени t1; t2;… ;tn, а от длительности временных промежутков τi: 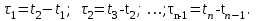 В частности, одномерная плотность распределения вообще не зависит от времени t: 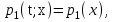 двумерная плотность сечений в моменты времени t1 и t2 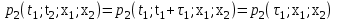 n-мерная плотность сечений в моменты времени t1; t2...; tn: 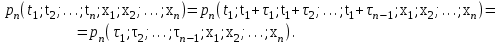 Случайный процесс Х(t) называется стационарным в широком смысле, если его моменты первого и второго порядка инвариантны относительно временного сдвига, то есть его математическое ожидание не зависит от времени t и является константой, а корреляционная функция зависит только от длины временного промежутка между сечениями: 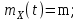 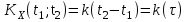 Очевидно, что стационарный случайный процесс в узком смысле является стационарным случайным процессом и в широком смысле; обратное утверждение не верно. 5.2 Свойства вероятностных характеристик стационарного случайного процесса1. 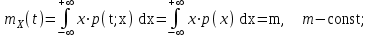 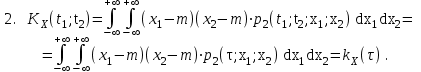 3. Корреляционная функция стационарного случайного процесса четна: 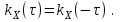 4. Дисперсия стационарного случайного процесса есть константа, равная значению ее корреляционной функции в точке  : :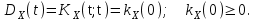 5. 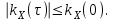 6. Корреляционная функция стационарного случайного процесса является положительно определенной, то есть 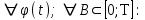 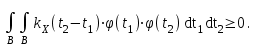 Нормированная корреляционная функция стационарного случайного процесса  также четна, положительно определена и при этом также четна, положительно определена и при этом  5.3. Стационарно связанные случайные процессы. Производная и интеграл от стационарного случайного процессаCлучайные процессы X(t) и Y(t) называются стационарно связанными, если их взаимная корреляционная функция зависит только от разности аргументов τ =t2-t1:  RXY(t1;t2)=rXY(τ). RXY(t1;t2)=rXY(τ).Стационарность самих случайных процессов X(t) и Y(t) не означает их стационарной связанности. Отметим основные свойства стационарно связанных случайных процессов, производной и интеграла от стационарных случайных процессов, 1) rXY(τ)=rYX(-τ). 2) 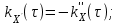 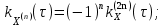 3) 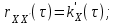 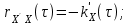 4) 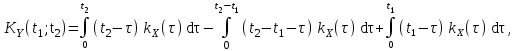 где 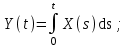 5) 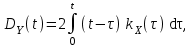 где где 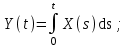 6)  ; ;  5.4. Эргодические стационарные случайные процессы и их характеристикиСреди стационарных случайных процессов есть особый класс процессов, называемых эргодическими, которые обладают следующим свойством: их характеристики, полученные усреднением множества всех реализаций, совпадают с соответствующими характеристиками, полученными усреднением по времени одной реализации, наблюдаемой на интервале (0, T) достаточно большой продолжительности. То есть на достаточнобольшом временном промежутке любая реализация проходит через любое состояние независимо от того, каково было исходное состояние системы при t=0; и в этом смысле любая реализация полностью представляет всю совокупность реализаций. Эргодическая теорема Биркгофа-Хинчина Для любого стационарного случайного процесса в узком смысле X(t), имеющего конечное математическое ожидание 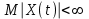 с вероятностью 1 существует предел с вероятностью 1 существует предел для ССП с непрерывным временем, для ССП с непрерывным временем,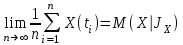 для ССП с дискретным временем. для ССП с дискретным временем.Если при этом X(t) – эргодический стационарный случайный процесс, то  В условии теоремы 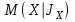 - условное математическое ожидание случайного процесса X(t)относительно Jx; Jx – - условное математическое ожидание случайного процесса X(t)относительно Jx; Jx –  -алгебра инвариантных по отношению к X(t)событий; событие А называется инвариантным относительно X(t), если -алгебра инвариантных по отношению к X(t)событий; событие А называется инвариантным относительно X(t), если 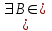 B B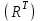 такое, что A={ω: X(ω,t) такое, что A={ω: X(ω,t)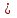 B}. B}.Достаточные условия эргодичности Теорема 1. Стационарный случайный процесс X(t) эргодичен относительно математического ожидания, если его корреляционная функция 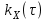 стремится к нулю при τ→∞; стремится к нулю при τ→∞;при этом: 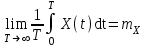 . .Теорема 2. Стационарный случайный процесс X(t) эргодичен относительно дисперсии, если корреляционная функция стационарного слу- чайного процесса Y(t)=X2(t) стремится к нулю при τ→∞; при этом: 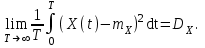 Теорема 3. Стационарный случайный процесс X(t) эргодичен относительно корреляционной функции, если стремится к нулю при τ→∞ кор- реляционная функция стационарного случайного процесса Z(t, τ)= 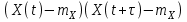 ; ;при этом: 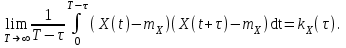 При практических расчетах интервал (0;Т) разбивается на n равных частей 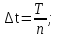 в каждом промежутке выбирается точка ti(например, середина). Если ограничиться формулой прямоугольников, получаем в каждом промежутке выбирается точка ti(например, середина). Если ограничиться формулой прямоугольников, получаем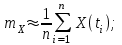  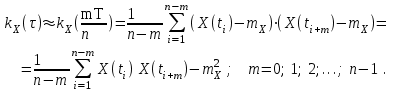 |
