Трапеция. Определение Трапеция
 Скачать 49.42 Kb.
|
|
1. Трапеция и её виды Определение Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие – нет. На Рис. 1. изображена произвольная трапеция. 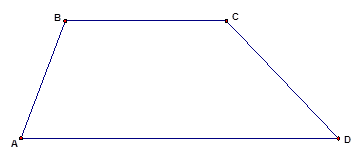 – это боковые стороны (те, которые не параллельны).  – основания (параллельные стороны). Рис. 1. Трапеция Если сравнивать трапецию с параллелограммом, то у параллелограмма две пары параллельных сторон. То есть параллелограмм не является частным случаем трапеции, так как в определении трапеции чётко сказано, что две стороны трапеции не параллельны. Выделим некоторые виды трапеции (частные случаи): равнобедренная (равнобокая) трапеция: боковые стороны равны; прямоугольная трапеция: один из углов равен  (из определения трапеции и свойства параллельных прямых следует, что два угла будут по ).2. Средняя линия трапеции и её свойства Определение Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. На Рис. 2. изображена трапеция со средней линией  . Рис. 2. Средняя линия трапеции Свойства средней линии трапеции: 1. Средняя линия трапеции параллельна основаниям трапеции. Доказательство: Пусть середина боковой стороны  трапеции  – точка  . Проведём через эту точку прямую, параллельную основаниям. Эта прямая пересечёт вторую боковую сторону трапеции  в точке  .По построению:  . По теореме Фалеса из этого следует:  . Значит, – середина стороны . Значит, – средняя линия.Доказано. 2. Средняя линия трапеции равна полусумме оснований трапеции:  .Доказательство: Проведём среднюю линию трапеции и одну из диагоналей: например, 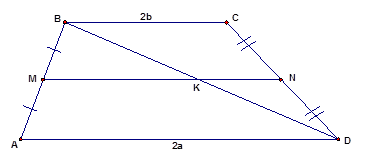 (см. Рис. 3). Рис. 3 По теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Так как равны отрезки:  . Значит, отрезок  является средней линией треугольника  , а отрезок  – средней линией треугольника  .Значит,  .Примечание: это следует из свойства средней линии треугольника: средняя линия треугольника параллельна основанию и равна его половине. Первая часть этого свойства доказывается аналогично с доказательством первого свойства средней линии трапеции, а вторую часть можно доказать (к примеру, для средней линии треугольника ), проведя через точку прямую, параллельную . Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.Получаем:  .Доказано. 3. Признаки равнобедренной трапеции Напомним, что равнобедренная трапеция – трапеция, у которой боковые стороны равны. Рассмотрим свойства боковой трапеции. 1. Углы при основании равнобедренной трапеции равны. Доказательство: Выполним стандартное дополнительное построение, которое очень часто используется при решении различных задач на трапецию: проведём прямую 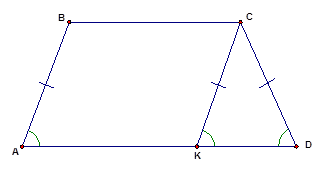 параллельно боковой стороне (см. Рис. 4). Рис. 4  – параллелограмм.Отсюда следует, что:  . Значит, треугольник  – равнобедренный. А значит, углы при его основании равны, то есть:  (последние два угла равны, как соответственные при параллельных прямых  ).Доказано. 2. Диагонали равнобедренной трапеции равны. Доказательство: Для доказательства этого свойства воспользуемся предыдущим. Действительно, рассмотрим треугольники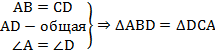: и  (см. Рис. 5.). Рис. 5  (по первому признаку равенства треугольников: две стороны и угол между ними).Из этого равенства сразу следует, что:  .Доказано. Оказывается, что, как и в случае с параллелограммом, у равнобедренной трапеции свойства одновременно являются и признаками. Сформулируем и докажем эти признаки. |