Главная страница
Навигация по странице:

  • Как провести эксперимент в домашних условиях при дистанционном обучении

  • Подвесьте его на нити, закрепив нить так, чтобы колебания происходили свободно. (Можно закрепить на ручке двери или окна).

  • Результаты занесите в таблицу, сделайте расчеты, напишите вывод по работе.

    		•

    Лабораторная работа_Янбердин. Определение ускорения свободного падения с помощью математического маятника


    Скачать 131.6 Kb.
    НазваниеОпределение ускорения свободного падения с помощью математического маятника
    Дата26.01.2022
    Размер131.6 Kb.
    Формат файлаdocx
    Имя файлаЛабораторная работа_Янбердин.docx
    ТипДокументы
    #343228

    Определение ускорения свободного падения с помощью математического маятника

    Оборудование: кронштейн с подвешенным на нем маятником на нити. В качестве подвешенного тела используется небольшой шарик

    Теоретические замечания

    Математическим маятником принято считать модель маятника, у которого длина подвеса во много раз больше линейных размеров подвешенного тела, а масса подвеса пренебрежимо мала по сравнению с массой подвешенного тела. Т.е. математический маятник – это материальная точка, подвешенная на невесомой нити. Колебания маятника происходит под действием силы тяжести, сила сопротивления среды (воздуха) считается бесконечно малой, т.е. ей можно пренебречь.

    Вывод рабочей формулы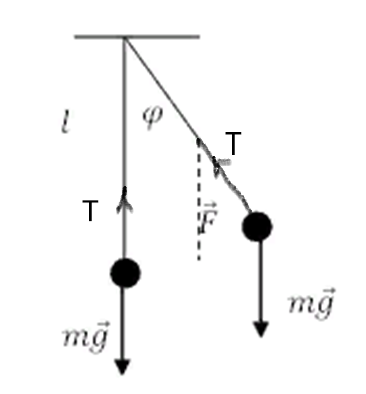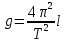





    ,

    Где l – длина нити,

    Т – период колебаний маятника

    Период колебаний определяется по формуле периода T = t/N, где

    t – полное время колебаний

    N – количество полных колебаний.

    Как провести эксперимент в домашних условиях при дистанционном обучении:

    1. Возьмите нить длиной 30 – 50 см и привяжите к ней небольшое и достаточно тяжелое по сравнению с массой нити тело (кольцо, монета, гайка…).

    2. Подвесьте его на нити, закрепив нить так, чтобы колебания происходили свободно. (Можно закрепить на ручке двери или окна).

    3. Отклоните от положения равновесия на небольшой угол (не более 15 градусов) и одновременно отсчитывайте количество колебаний и время колебаний по секундомеру. Желательно сделать 10-15 полных колебаний маятника.

    4. Результаты занесите в таблицу, сделайте расчеты, напишите вывод по работе.

    Результаты эксперимента по определению ускорения свободного падения с помощью математического маятника

    Ход работы:

    1. Определяем период колебаний по формуле периода:

    T = t/N.

    1. Ускорение свободного падения находим по формуле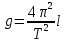

    :

    1. Определяем среднее арифметическое значение gср по формуле:



    1. Находим отклонение от среднего среднего арифметического значения ускорения свободного падения ⃒Δg⃒:

    2. Найдем среднюю квадратичную ошибку среднего арифметического значения ускорения свободного падения ⃒Δg⃒ср: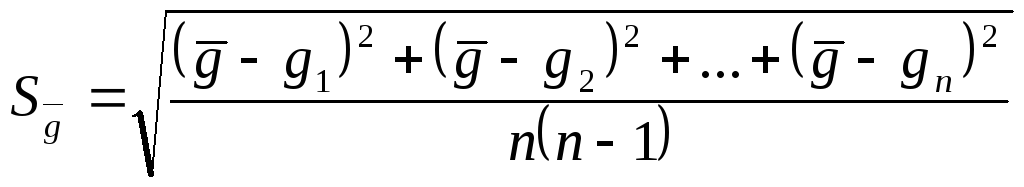



    1. Вычисляем погрешность δg по формуле: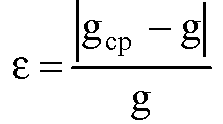



    Все вычисления сделаны в EXCEL и приведены в таблице 1.

    Таблица 1- Результаты вычислений

    l
    N
    t, c
    N
    T, c
    g, м/с2
    gср, м/с2
    ⃒Δg⃒, м/с2
    ⃒Δg⃒ср, м/с2
    δg, %

    0,5
    1
    16
    12
    1,33
    11,092
    9,654
    1,438
    0,093
    1,588%




    2
    17
    1,42
    9,825
    0,171




    3
    17
    1,42
    9,825
    0,171




    4
    18
    1,5
    8,764
    -0,890




    5
    18
    1,50
    8,764
    -0,890

    Вывод: в результате выполнения работы было определено ускорение свободного падения. Его значение (9,65±0,09) м/с2. Отличается от известного на 1,59 %. Погрешности измерений вызваны погрешностью секундомера, неоднородностью земной поверхности, географической широтой местности, а также высотой помещения, в котором проводились измерения, над поверхностью земли.

    написать администратору сайта