|
|
Дз. +дз_1[1]. Определите длину кратчайшего маршрута между пунктами г и З. Передвигаться можно только по указанным дорогам
12
|
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах). Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда.
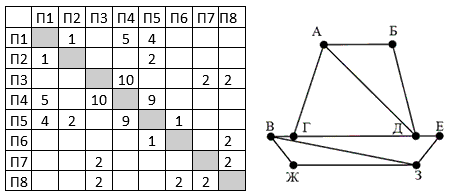 Определите длину кратчайшего маршрута между пунктами Г и З. Передвигаться можно только по указанным дорогам.
|
26400
|
В файле 3-3.xls приведён фрагмент базы данных «Оператор» об оказанных услугах. База данных состоит из трёх таблиц. Таблица «Клиенты» содержит записи об абонентах, которым были оказаны услуги. О каждом абоненте содержится следующая информация: район, в котором проживает абонент, адрес (улица и дом) и фамилия с инициалами. Таблица «Услуги» содержит записи об оказываемых оператором услугах - наименование и цена оказанной услуги. Таблица «Оказанные услуги» содержит информацию о том когда (поле дата), кому (ID клиента) и какая услуга (ID услуги) была оказана. На рисунке приведена схема базы данных.
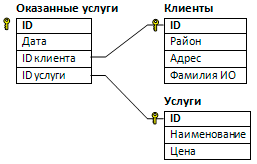 Используя информацию из приведённой базы данных, суммарную выручку оператора за оказанные услуги в Центральном и Речном районе в период с 4 по 9 августа (включительно). В ответе запишите только число.
|
15
|
Для кодирования некоторой последовательности, состоящей из букв Н, Г, В, А, Р, И, К, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Известно, что слово КАНАВКА закодировано с помощью битовой последовательностью минимальной длины. Укажите эту длину.
|
87
|
Компьютер по имени Иннокентий преобразует натуральное число N по следующим правилам и получает число R:
1) Строится двоичная запись числа N.
2) Если количество цифр в двоичной записи числа N четно, то справа приписывается 10, если нечётно, то слева приписывается 11.
Полученная таким образом запись является двоичной записью искомого числа R. Найдите количество чисел N из отрезка [100; 200], для которых результат работы компьютера будет четным.
|
90
|
Изображение было оцифровано и сохранено в виде растрового файла. Получившейся файл был передан в город А по каналу связи за 30 секунд. Затем то же изображение было оцифровано повторно с разрешением в 3 раза больше и глубиной кодирования цвета в 2 раза меньше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б, пропускная способность канала связи с городом Б в 1.5 раза выше, чем канала связи с городом А. Сколько секунд длилась передача файла в город Б?
|
4080
|
Маша составляет 7-буквенные коды из букв В, Е, Н, Т, И, Л, Ь. Каждую букву нужно использовать ровно 1 раз, при этом буква Ь не может стоять на последнем месте и между гласными. Сколько различных кодов может составить Маша?
|
754
|
Откройте файл электронной таблицы 9-119.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью длин отрезков ломаной. Выясните, какое количество четверок чисел может являться сторонами параллелограмма. В ответе запишите только число.
|
33
|
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «мысль» или «Мысль» (в любом падеже единственного и множественного числа) в тексте романа А.С. Пушкина «Капитанская дочка» (файл 10-34.docx). В ответе укажите только число.
|
160
|
В некоторой стране автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 19 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным целым количеством байт. Определите объем памяти в байтах, необходимый для хранения 40 автомобильных номеров.
|
|
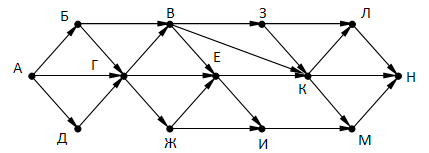
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город Н и проходящих через пункт Г или через пункт Е, но не через оба этих пункта?
|
|
Значение арифметического выражения: 3610 + 625 – 15 записали в системе счисления с основанием 6. Сколько цифр «0» в этой записи?
|
|
В файле 17-205.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от –10 000 до 10 000 включительно. Определите количество пар, в которых хотя бы один из двух элементов заканчивается на 7, а их сумма делится на 12. В ответе запишите два числа: сначала количество найденных пар, а затем – максимальную сумму элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
|
|
Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку; по команде вниз – в соседнюю нижнюю. Исключением являются клетки, отмеченные желтым цветом. Находясь в них, робот не может выполнять команду вправо.
Перед запуском Робота в каждой клетке квадрата указан бонус, который Робот забирает после посещения клетки. Размер бонуса в каждой клетке – это натуральное число, не превышающее 100. Это правило относится к начальной и конечной клеткам маршрута Робота.
Определите минимальную и максимальную суммы бонусов, которые может собрать Робот, перемещаясь из левой верхней клетки квадрата в его правую нижнюю клетку. В ответе укажите два числа: сначала минимальную сумму, затем максимальную.
Исходные данные для Робота записаны в файле 18-130.xls в виде прямоугольной таблицы, каждая ячейка которой соответствует клетке квадрата. Пример входных данных:
 Для указанных входных данных ответом является пара чисел: 27 41.
|
|
В файле 22-40.xls содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Если процесс B зависит от процесса A, то процесс B может начать выполнение не раньше, чем через 3 мс после завершения процесса A. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите, за какое минимальное время можно выполнить все процессы. В ответе запишите целое число – минимальное время в мс.
Типовой пример организации данных в файле:
ID процесса B
|
Время выполнения процесса B (мс)
|
ID процесса(ов) A
|
1
|
4
|
0
|
2
|
3
|
0
|
3
|
1
|
1; 2
|
4
|
7
|
3
|
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2 и 3 мс ожидания, то есть, через 7 мс после старта. Он длится 1 мс и закончится через 7 + 1 = 8 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3 и 3 мс ожидания, то есть, через 11 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 11 + 7 = 18 мс.
|
|
В файле 22-29.xls содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B требуется, чтобы был выполнен хотя бы один из процессов А. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
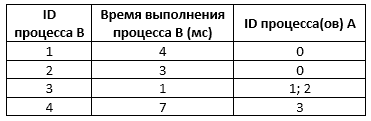 В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения процесса 1 или 2, то есть, через 3 мс после старта. Он длится 1 мс и закончится через 3 + 1 = 4 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 4 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 4 + 7 = 11 мс.
|
|
В файле 22-38.xls содержится информация о совокупности N вычислительных процессов, которые могут выполняться параллельно или последовательно. Будем говорить, что процесс B зависит от процесса A, если для выполнения процесса B необходимы результаты выполнения процесса A. В этом случае процессы могут выполняться только последовательно. Информация о процессах представлена в файле в виде таблицы. В первом столбце таблицы указан идентификатор процесса (ID), во втором столбце таблицы – время его выполнения в миллисекундах, в третьем столбце перечислены с разделителем «;» ID процессов, от которых зависит данный процесс. Если процесс является независимым, то в таблице указано значение 0.
Определите минимальное время, через которое завершится выполнение всей совокупности процессов, при условии, что все независимые друг от друга процессы могут выполняться параллельно.
Типовой пример организации данных в файле:
В данном случае независимые процессы 1 и 2 могут выполняться параллельно, при этом процесс 1 завершится через 4 мс, а процесс 2 – через 3 мс с момента старта. Процесс 3 может начаться только после завершения обоих процессов 1 и 2, то есть, через 4 мс после старта. Он длится 1 мс и закончится через 4 + 1 = 5 мс после старта. Выполнение процесса 4 может начаться только после завершения процесса 3, то есть, через 5 мс. Он длится 7 мс, так что минимальное время завершения всех процессов равно 5 + 7 = 12 мс.
|
|
В файле 17-282.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 10 000. Определите количество пар элементов последовательности, в которых хотя бы одно число кратно максимальному числу в последовательности, кратному 13. В ответе запишите количество найденных пар, затем минимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
|
|
В файле 17-344.txt содержится последовательность целых чисел. Элементы последовательности – натуральные числа, не превосходящие 100000. Определите количество пар последовательности, в которых сумма чисел четна, а разница между числами кратна минимальному числу, кратному 103. Гарантируется, что элемент, кратный 103, в последовательности есть. В ответе запишите количество найденных пар, затем максимальную из сумм элементов таких пар. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.
| |
|
|
Скачать 49.25 Kb.