4 вар. Определите форму, способ и виды следующего статистического наблюдения

• Название: Определите форму, способ и виды следующего статистического наблюдения
• Дата: 05.10.2022
• Размер: 54.56 Kb.
• Имя файла: 4 вар.docx
• Тип: Задача; #715942

СОДЕРЖАНИЕ
Задание 1 3

Задание 2 4

Задание 3 9

Список литературы 12
Задание 1:

Определите форму, способ и виды следующего статистического наблюдения:

— обследование численности промышленно-производственного персонала.

Ответ:

При обследовании численности промышленно-производственного персонала применяют следующую форму: специально организованное наблюдение. Проводится с целью получения данных, которые в силу тех или иных причин не вошли в отчетность или для проверки данных отчетности. Представляет собой сбор данных посредством переписей и единовременных учетов.

Статистические наблюдения подразделяются на виды по следующим признакам:

— по времени регистрации данных проводится текущее (непрерывное) наблюдение — проводится для изучения текущих явлений и процессов. Регистрация фактов осуществляется по мере их свершения;

по полноте охвата единиц совокупности проводится метод основного массива — состоит в изучении самых существенных, наиболее крупных единиц совокупности, имеющих по основному признаку наибольший удельный вес в изучаемой совокупности;

Способ статистического наблюдения — непосредственное статистическое наблюдение — наблюдение, при котором сами регистраторы путем непосредственного замера, взвешивания, подсчета устанавливают факт подлежащий регистрации.
Задача 2:

Построить интервальный вариационный ряд распределения студентов по количеству пропущенных часов занятий.

16	10	6	30	18	11	5	23
22	8	12	20	16	17	31	22
14	4	13	15	24	9	30	36
18	33	28	19	27	7	11	35

Количество групп 6.

По данным группировки определите среднюю величину признака, показатели вариации, моду, медиану, относительный показатель структуры, построить структурную диаграмму. Определить с вероятностью 0,954 пределы средней величины количества пропущенных часов во всей совокупности, принимая, что представленные данные являются выборочной совокупностью и составляют 15% от генеральной совокупности.

Решение:

Все показатели запишем в таблицу 1

Определим интервал:

i= 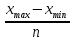= =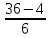5.3

Таблица 1 - расчета показателей.

Группы	Середина интервала, xцентр	Кол-во, fi	xi·fi	Накопленная частота, S	|x-xср|·fi	(x-xср)2·fi	Относительная частота, fi/f
4 - 9.4	6.7	6	40.2	6	70.106	819.148	0.188
9.3 – 14.7	12	6	72	12	38.006	240.746	0.188
14.7 – 20.1	17.4	8	139,2	20	7.875	7.752	0.25
20.1 – 25.4	22.75	4	91	24	17.463	76.235	0.125
25.4 – 30.7	28.05	4	112,2	28	38.663	373.697	0.125
30.7 - 36	33.35	4	133,4	32	59.863	895.88	0.125
Итого		32	588.3		231.975	2413.457	1

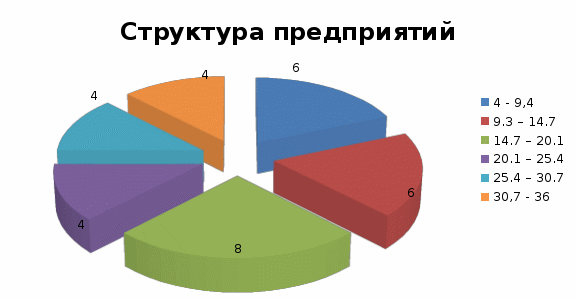Для оценки ряда распределения найдем следующие показатели:

1. 
   Показатели центра распределения.
   

Средняя взвешенная (выборочная средняя)

Мода.

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.
где x₀ – начало модального интервала; h – величина интервала; f₂ –частота, соответствующая модальному интервалу; f₁ – предмодальная частота; f₃ – послемодальная частота.

Выбираем в качестве начала интервала 7.92, так как именно на этот интервал приходится наибольшее количество.
Наиболее часто встречающееся значение ряда – 16.5

Медиана.

Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.

Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных.

В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 7.92 - 9.33, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).


Таким образом, 50% единиц совокупности будут меньше по величине 17.4.

В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (x_ср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(x_ср-Me) ≈ x_ср-Mo

2. 
   Показатели вариации.
   

Абсолютные показатели вариации.

Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.

R = x_max - x_min = 36-4 = 32

Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

Каждое значение ряда отличается от другого в среднем на 7.2

Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 18.4 в среднем на 8.684

Относительные показатели вариации.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.

Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
Поскольку v>30% ,но v<70%, то вариация умеренная.

Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней.
Определим дисперсию среднего значения признака выборки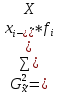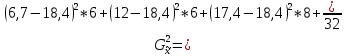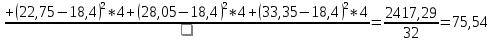

;





Определим предельную ошибку выборки: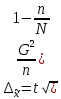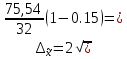

)

2,82

Определим пределы нахождения среднего значения: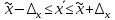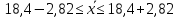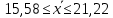







Задача 3:

Имеются следующие данные о производстве молока в России за 1990-1995 гг., млн. т.:

1990	1991	1992	1993	1994	1995
13,3	13,5	14,8	16,1	16,6	16,4

Установите начальный, конечный и базисный уровни ряда динамики для определения:

1. 
   среднего уровня ряда;
   
2. 
   цепных и базисных абсолютных приростов;
   
3. 
   цепных и базисных темпов роста;
   

Определите для каждого года абсолютное значение 1% прироста. Результат расчетов изложите в табличной форме.

год	Кол-во	Абсолютные приросты, млн. т.		абсолютное значение 1% прироста	Темп роста,%
		базисный	цепной		базисный	цепной
1990	13,3
1991	13,5	0,2	0,2	0,133	101,5	101,5
1992	14,8	1,5	1,3	0,135	111,28	109,63
1993	16,1	2,8	1,3	0,148	121,06	108,78
1994	16,6	3,3	0,5	0,161	124,81	103,11
1995	16,4	3,1	-0,2	0,166	123,31	98,8

Решение:

1. 
   Определим средний уровень ряда: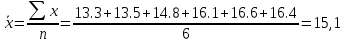
   

млн. т.

2. 
   Определим цепные и базисные абсолютные прироста:
   

а. базисный абсолютный темп прироста:

у_б=у_n-y_o

у_{б 1991}=13,5-13,3 = 0,2 млн.т.;

у_{б 1992}=14,8-13,3 = 1,5 млн.т.;

у_{б 1993}=16,1-13,3 = 2,8 млн.т.;

у_{б 1994}=16,6-13,3 = 3,3 млн.т.;

у_{б 1995}=16,4-13,3 = 3,1 млн.т.;
б. цепной абсолютный прирост:

у_б=у_n+y_n-1

у_{б 1991}=13,5-13,3 = 0,2 млн.т.;

у_{б 1992}=14,8-13,5 = 1,3 млн.т.;

у_{б 1993}=16,1-14,8 = 1,3 млн.т.;

у_{б 1994}=16,6-16,1 = 0,5 млн.т.;

у_{б 1995}=16,4-16,6 = - 0,2 млн.т.;

Абсолютное значение 1% прироста рассчитывается только для цепных показателей

%= 1%*у_n-1

%₁₉₉₁=0,01*13,3= 0,133 млн.т.;

%₁₉₉₂=0,01*13,5= 0,135 млн.т.;

%₁₉₉₃=0,01*14,8= 0,148 млн.т.;

%₁₉₉₄=0,01*16,1= 0,161 млн.т.;

%₁₉₉₅=0,01*16,6= 0,166 млн.т.

3. 
   Определим цепные и базисные темпы роста:
   

а. базисный темп роста:

Т_рб= ;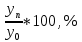

Т_рб=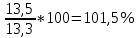

Т_рб=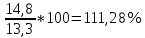

Т_рб=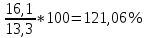

Т_рб=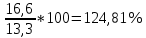

Т_рб=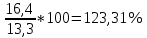

б. цепной темп роста:

Т_рц= ;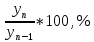

Т_рц= ;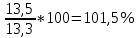

Т_рц= ;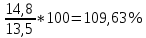

Т_рц= ;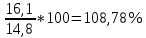

Т_рц= ;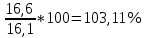

Т_рц= ;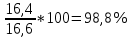


СПИСОК ЛИТЕРАТУРЫ

1. 
   Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под. ред. чл.-корр. РАН И.И. Елисеевой. – М.: Финансы и статистика, 2004. 2.
   
2. 
   Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. – М.: ИНФРА-М, 2004. 3.
   
3. 
   Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2004. 4.
   
4. 
   Практикум по теории статистики: Учеб. пособие / Под.ред. проф. Р.А. Шмойловой. – М.: Финансы и статистика, 2004. 5.
   
5. 
   Статистический словарь / Гл. ред. М.А. Королев. – М.: Финансы и статистика, 1989. 6.
   
6. 
   Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: Учебник / Под ред. проф. Шмойловой Р.А. – М.: Финансы и статистика, 2004. 7.
   
7. 
   Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере / Под ред. В.Э.Фигурнова. – М.: ИНФРА-М, Финансы и статистика, 1998.