Задачи по инвестиционному анализу. задачи1 2. Определить, какая из ценных бумаг является более привлекательной с точки зрения минимизации риска. По акциям компании а ожидается доходность в размере 71222% с вероятностью ее получения соответственно 304030%,
 Скачать 94.45 Kb.
|
|
Определить, какая из ценных бумаг является более привлекательной с точки зрения минимизации риска. По акциям компании А ожидается доходность в размере 7-12-22% с вероятностью ее получения соответственно 30-40-30%, по акциям компании В ожидается доходность 10-15-22% годовых с вероятностью 20-30-50% соответственно. РешениеДля того, чтобы определить, какая из ценных бумаг является более привлекательной с точки зрения минимизации риска необходимо оценить вероятностное распределение доходности, для чего рассчитывается коэффициент вариации доходности (СV): CV=σd где – стандартное отклонение доходности ценной бумаги (d) от ее наиболее вероятной (ожидаемой) доходности d, % . Стандартное отклонение доходности i-й ценной бумаги: σ=i=1n(di-d)2*pi Ожидаемая величина доходности: d=i=1ndi*pi где di – прогнозные оценки значений доходности по i-й ценной бумаге, %; Pi – вероятность получения дохода в i-й экономической ситуации, коэф. Рассчитаем для каждой компании: А: d=7*0,3+12*0,4+22*0,3=13,5 % В: d=10*0,2+15*0,3+22*0,5=17,5% А: σ=7-13,52*0,3+12-13,52*0,4+22-13,52*0,3=5,94 В: σ=10-17,52*0,2+15-17,52*0,3+22-17,52*0,5=4,82 А: CV=5,94*100%13,5=43,98% В: CV=4,82*100%17,5=27,55% Ответ: менее рискованна покупка акций В, при этом средняя ожидаемая доходность акций В также значительно выше средней ожидаемой доходности акций А 2. Проанализировать риск инструментов, а также возможных портфелей. Исходные данные
Портфели «А+В» и «В+С» менее рискованны, чем сами активы, входящие в их состав Наиболее рискованным является актив B, при этом он входит в состав наименее рискованного портфеля «А+В». То есть в зависимости от комбинации активов меняется и средняя доходность, и риск портфеля. Объединение активов в портфель приводит к снижению риска. Если на данном примере делать выбор между портфелями, то ответ будет зависеть от поставленной цели. Так, наиболее привлекательным активом с позиции минимизации риска является портфель «А+В», а с позиции максимизации дохода — портфель, состоящий только из актива А. Определите ковариацию и коэффициент корреляции для активов А и В, статистика доходности которых представлена в таблице.
Решение Коэффициент выборочной ковариации рассчитывается по формуле:  Средняя доходность актива А: 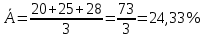 Средняя доходность актива В: 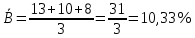 Рассчитываем коэффициент выборочной ковариации: 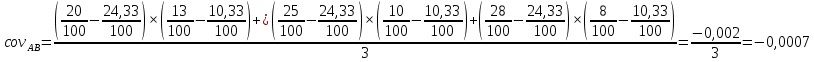 Вывод: поскольку ковариация отрицательна, то при изменении значения одной переменной другая имеет тенденцию изменяться в том же направлении. Коэффициент корреляции рассчитывается по формуле: 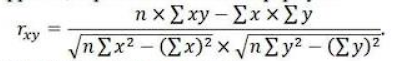 Рассчитываем вспомогательные величины: 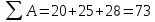 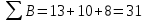 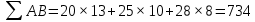 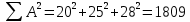 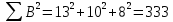 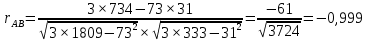 Вывод: поскольку коэффициент корреляции меньше 0, значит возникает отрицательная корреляция. Это указывает на то, что обе переменные движутся в противоположном направлении. Любое значение от 0 до -1 означает, что два актива движутся в противоположных направлениях. Ответ: -0,0007, -0,999. Определите ковариацию и коэффициент корреляции для активов А и В, статистика доходности которых представлена в таблице.
Решение Коэффициент выборочной ковариации рассчитывается по формуле: Средняя доходность актива А: 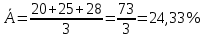Средняя доходность актива В: 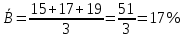 Рассчитываем коэффициент выборочной ковариации: 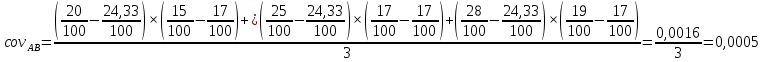 Вывод: поскольку ковариация положительна, то при изменении значения одной переменной другая имеет тенденцию изменяться в том же направлении. При положительной ковариации доходностей двух бумаг с ростом доходности первой бумаги доходность второй также будет расти. Коэффициент корреляции рассчитывается по формуле: 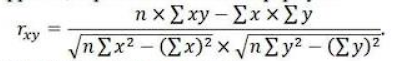Рассчитываем вспомогательные величины: 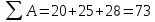 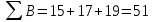 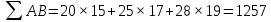 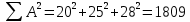 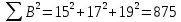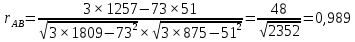Вывод: поскольку коэффициент корреляции больше 0, значит возникает положительная корреляция. Это указывает на то, что обе переменные движутся в одном направлении, доходность активов при одних и тех же условиях изменяется в одном направлении. Ответ: 0,0005, 0,989. Определить уровень риска портфеля, включающего следующие активы: 2% акции компании A, имеющие β =1,8; 60% акции компании B, имеющие β =0,8; 30% акции компании C, имеющие β =1; 8% акции компании D, имеющие β =1,1. Решение Уровень портфельного риска в этом случае оценивается по методу средневзвешенной. В этом случае формула принимает вид: 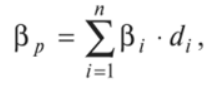 где 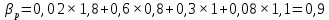 - значение бета-коэффициента i-го актива в портфеле; - значение бета-коэффициента портфеля; - доля i-го актива в портфеле; Вывод: поскольку акции компании имеют 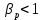 , значит риск портфеля ниже общерыночного уровня | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||