Вариант 8 контрольная тау. Kontrolnaya_rabota тау Вариант 8. Определить передаточные функции корректирующих звеньев (рис. )

• Название: Определить передаточные функции корректирующих звеньев (рис. )
• Анкор: Вариант 8 контрольная тау
• Дата: 07.11.2020
• Размер: 127.42 Kb.
• Имя файла: Kontrolnaya_rabota тау Вариант 8.docx
• Тип: Контрольная работа; #148669

Контрольная работа

Вариант 8

1. 
   Определить передаточные функции корректирующих звеньев (рис. 1.4.).
   

Рис. 1.4. Электрическая цепь R₁ = 400кОм R₂ = 133кОм С = 0,1 мкФ
Для электрической цепи а:

П 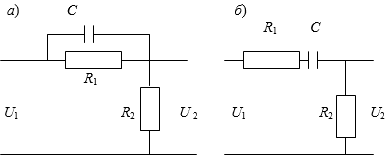ередаточная функция звена может быть найдена как отношение сопротивления элемента (или группы элементов) с которого снимается выходной сигнал к сумме сопротивлений всех элементов, последовательно включённых в контур: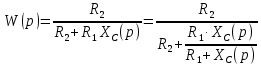

(1)

Зная, что реактивное сопротивление конденсатора описывается выражением: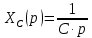

(2)

Подставим выражение (2) в (1):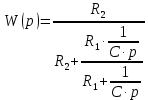

(3)
Сгруппируем коэффициенты относительно р: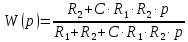

(4)

Подставляем числа из дано: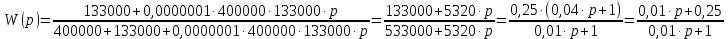


Для электрической цепи б:

Передаточная функция звена может быть найдена как отношение сопротивления элемента (или группы элементов), с которого снимается выходной сигнал к сумме сопротивлений всех элементов, последовательно включённых в контур: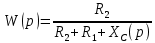

(5)

Подставляема выражение (2) в (5):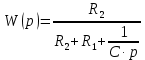

(6)

Сгруппируем коэффициент относительно р: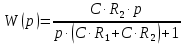

(7)

Подставляем числа из дано: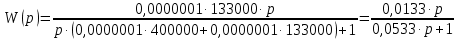

2. 
   Начертить АЧХ, ФЧХ, АФХ, ЛАЧХ, ЛФЧХ, исследуя передаточную функцию объекта, полученную в предыдущем задании.
   

В ходе выполнения первого задания получили следующие передаточные функции:

Для электрической цепи а: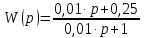



Тогда уравнение амплитудно–фазовой характеристики получим, заменив передаточной функции p на jω: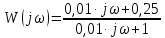



Избавимся от мнимой составляющей j, помножив на :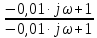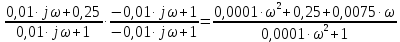



Уравнения вещественной и мнимой частотных характеристик: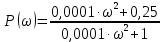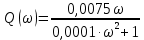



Уравнение и график амплитудно–частотной характеристики (АЧХ):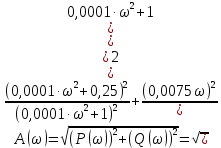



У 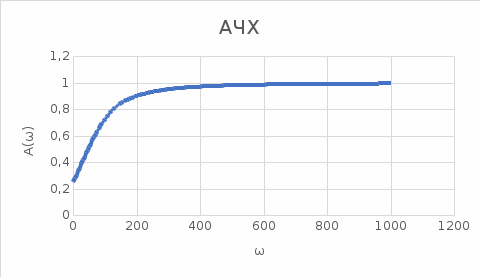равнение и график фазовой частотной характеристики (ФЧХ):





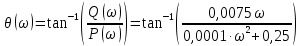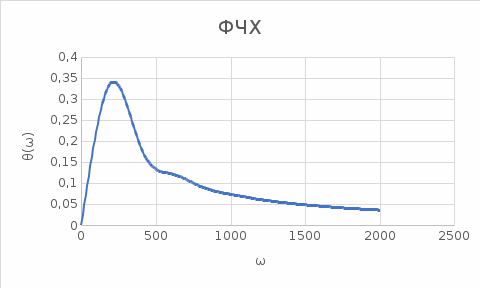Уравнение и график логарифмической амплитудно-частотной характеристики: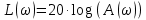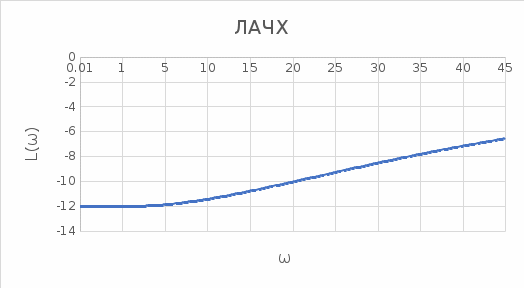





У 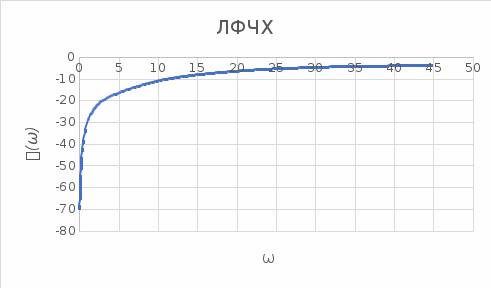равнение и график логарифмической фазовой частотной характеристики: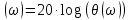



Для электрической цепи б: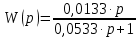



Уравнение амплитудно–фазовой характеристики получим, заменив передаточной функции p на jω: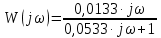



Избавимся от мнимой составляющей j, помножив на , :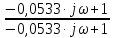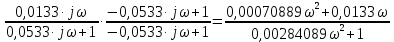



Уравнения вещественной и мнимой частотных характеристик: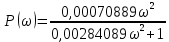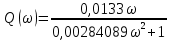



У 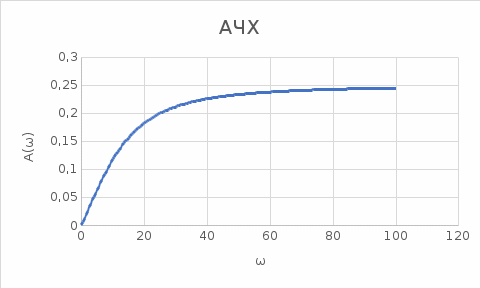равнение и график амплитудно–частотной характеристики (АЧХ):



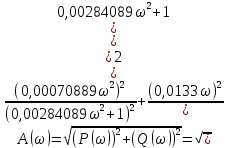Уравнение и график фазовой частотной характеристики (ФЧХ):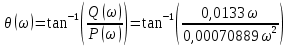



У 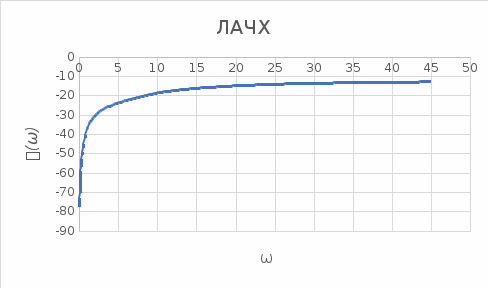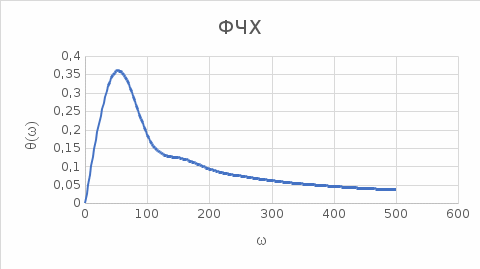равнение и график логарифмической амплитудно-частотной характеристики: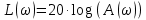



У 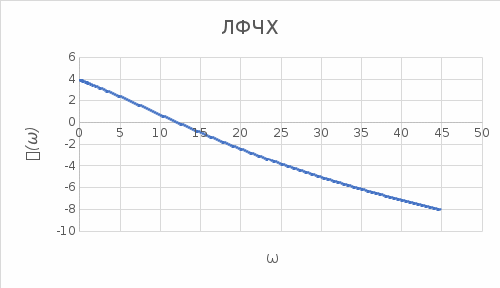равнение и график логарифмической фазовой частотной характеристики:

3. 
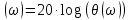   Составить передаточную функцию и дифференциальные уравнения замкнутой автоматической системы уравнения. Определить, какие элементарные звенья входят в состав САУ. Записать характеристическое уравнение замкнутой системы. Определить её устойчивость, используя алгебраический критерий Гурвица. Рассчитать критический коэффициент усиления разомкнутой САУ, т.е. коэффициент, при котором система окажется на границе устойчивости по Грувицу.
   

Вариант	W1(p)	W2(p)	W3(p)	W4(p)	W5(p)
8	1/(1+p)	10/(1+8p)	10p	12	1/p

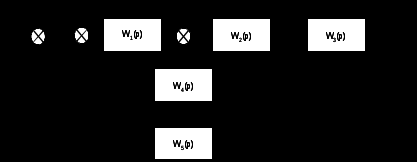Преобразуем схему. Перенесём звено W₁(p) через суммирующее звено против прохождения сигнала и добавим звено W₁(p) в контур обратной связи последовательно звену W₄(p):

П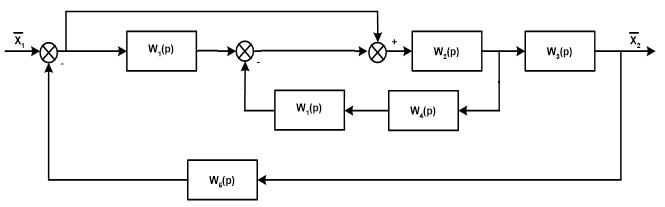
осле поменяем суммирующие звенья: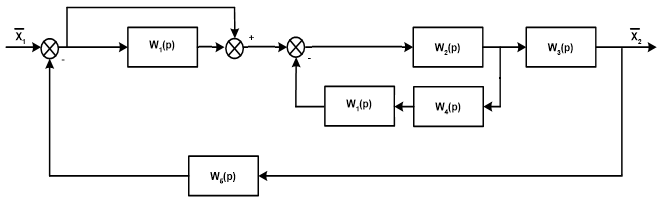




Заменим последовательное соединение звеньев W₁(p) и W₄(p) на одно звено W₇(p):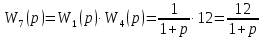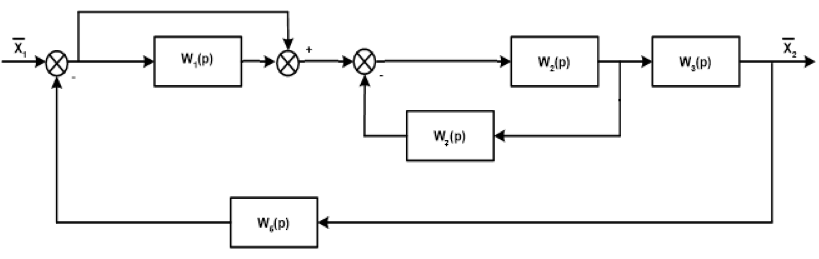




З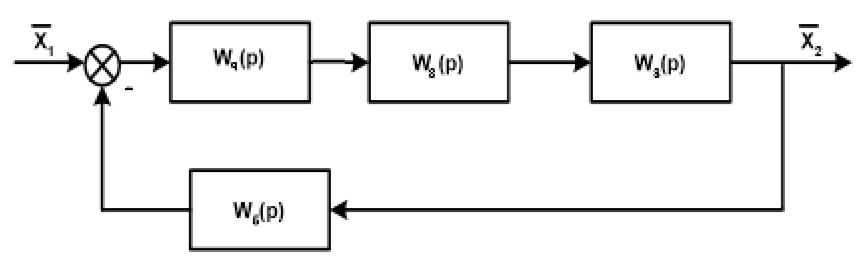
аменяем параллельное соединение с передаточными функциями W₂(p) и W₇(p) (отрицательная обратная связь) на одно звено W₈(p), а звено W₁(p) соединим с единичным звеном и меняем на W₉(p):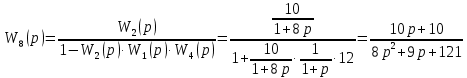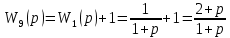





Схема сведена в замкнутый контур с отрицательной обратной связью.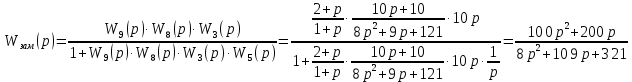



Для определения устойчивости системы воспользуемся критерием Гурвица. Для этого выделяем характеристический полином замкнутой системы, т.е. знаменатель передаточной функции замкнутой системы: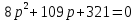



По критерию Гурвица, для систем с полиномом 2 порядка. Необходимым и достаточным условие устойчивости является положительность коэффициентов характеристических уравнений. В нашем случае, условие выполняется, следовательно замкнутая система устойчива.