Сопромат. Определить Величину и направление опорной реакции в заделке
 Скачать 227.66 Kb. Скачать 227.66 Kb.
|
|
Стальной стержень находится под действием продольных сил. Определить: 1. Величину и направление опорной реакции в заделке. 2. Построить эпюры внутренних продольных сил F 3. Для прямого стержня постоянного сечения подобрать размер стороны квадрата a квадратного сечения по условию прочности 4. Построить эпюры нормальных напряжений σ 5. Рассчитать деформацию участков и общее изменение длины  прямого стержня постоянного сечения прямого стержня постоянного сечения6. Рассчитать перемещения характерных сечений стержня постоянного сечения и построить их эпюру. Исходные данные: модуль нормальной упругости стали Е = 215000 МПа; длина стержня b = 0,55 м; коэффициент k = 0,4; величина силы F = 105 кН 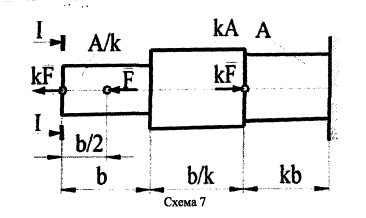 Рис. 1 – Схема стержня Решение 1. Для определения опорной реакции в заделке проведем ось X, направим силу реакции R в произвольном направлении и запишем уравнение статики, проецируя все силы на ось X. 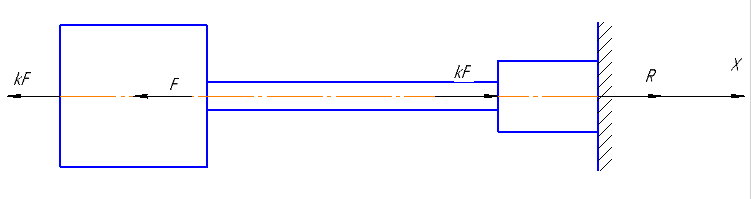 Рис.2 - Определение опорной реакции в заделке 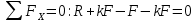 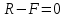 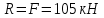 Положительный знак говорит о том, что направление указано верно. 2. Определяем методом сечений (алгоритм Р.О.З.У) продольные силы, действующие в поперечных сечениях стержня по участкам: Участок I. Рассекаем стержень в произвольном сечении на 1 участке. Отбрасываем правую часть стержня (на которую действуют активные силы и реакция в плоскости заделки). Заменяем действие отброшенной части на оставшуюся продольной силой N1, направленной от сечения (рисунок 3, a). Уравновешиваем оставшуюся часть. Для чего составляем уравнение равновесия из условия –  (ось координат Xнаправим вправо). (ось координат Xнаправим вправо).Получаем уравнение 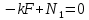  Повторяем процедуру метода сечений (см. рисунок 3,б) и составляем уравнение равновесия для II участка: 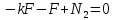 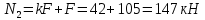 Участок III. Еще раз повторяем процедуру метода сечений (см. рисунок 3, в) и составляем уравнение равновесия для III участка: 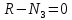 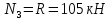 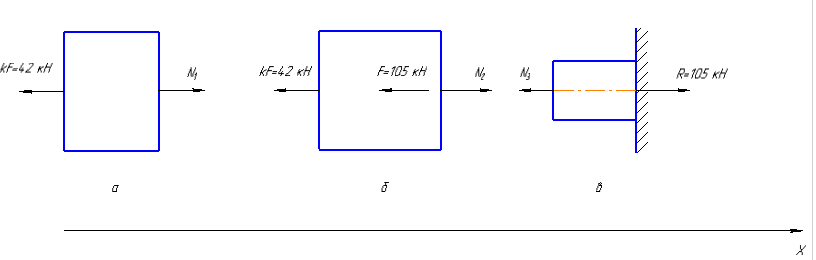 Рис. 3 – Алгоритм РОЗУ По полученным значениям с учетом их знаков строим эпюру продольных сил (рисунок 4). 3. Условие прочности при растяжении-сжатии  Тогда площадь сечения I-I равна:  В сечении I-I  , тогда площадь стержня: , тогда площадь стержня: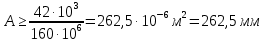 Зная площадь квадрата найдем сторону: 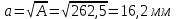 4. Определяем нормальные напряжения, действующие в поперечных сечениях стержня по соответствующим участкам по формуле: 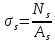 где s – номер участка Получаем 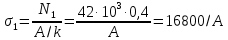  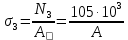 По полученным значениям с учетом их знаков строим эпюру нормальных напряжений (рисунок 4). 5. Определим абсолютные удлинения стержня на его границах, начиная с I участка, по формуле. 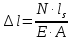 , где , где 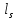 – длина соответствующего участка – длина соответствующего участка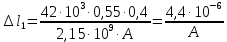 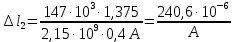  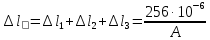 6. По полученным значениям с учетом их знаков строим эпюру перемещений поперечных сечений стержня, начиная с сечения в плоскости заделки, где Δl0= 0. (рисунок 4). 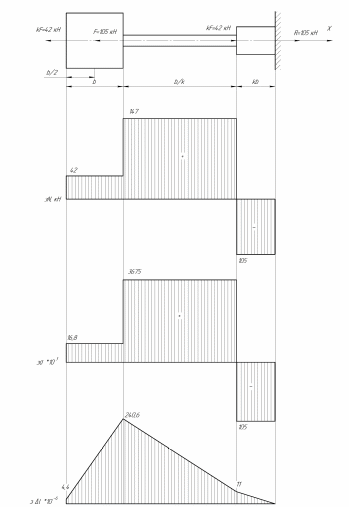 Рис.4 - Эпюры |
