Лабораторная работа по кинетическим реакциям. 4 вар.. Определить вид дифференциального кинетического уравнения и константу скорости реакции
 Скачать 27.36 Kb. Скачать 27.36 Kb.
|
|
Определить вид дифференциального кинетического уравнения и константу скорости реакции nA + mB → продукты если в трех опытах при начальных концентрациях вещества В = 0,2; 0,4; 0,6 моль/л и фиксированной концентрации вещества А, равной [A]0 = 1,2 моль/л, скорости реакции имели значения v1 = 0,23, v2 = 0,46, v3 = 0,69. В трех последующих опытах при различных начальных концентрациях [A] = 0,1; 0,3; 0,5 моль/л и постоянной концентрации В, равной [B]0 = 1,4 моль/л, скорости реакции имели значения v4 = 0,0112, v5 = 0,1010, v6 = 0,2850. Полученные данные представлены в табл. 1. Таблица 1
Определить вид дифференциального кинетического уравнения и константу скорости реакции. Решение. Зависимость начальной скорости от концентрации для данной реакции выражается дифференциальным кинетическим уравнением: v = k [A]n [B]m Прологарифмируем это выражение: lnv = lnk + n ln[A] + m ln[B] Величины к, п и т для рассматриваемой реакции (при Т = const) являются постоянными и не зависят от концентрации реагентов. Так как в трех опытах (1 - 3) концентрация вещества А постоянна (обозначим ее [А]0), то в уравнении сумма (lnk + n·ln[A]0) будет тоже величиной постоянной. Обозначим ее lnk + n·ln[A]0 = D1. Тогда уравнение можно переписать так: lnv = mln[B] + D1. Зависимость представляет собой в координатах ln[B] – ln и уравнение прямой линии, тангенс угла наклона которой к оси абсцисс равен порядку реакции по веществу В. В табл.2 представлены значения логарифмов концентраций и скоростей для опытов (1–6). Табл.2
По результатам опытов (1-3) строим график зависимости lnv от ln[B] и найдем порядок реакции по веществу B. 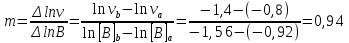 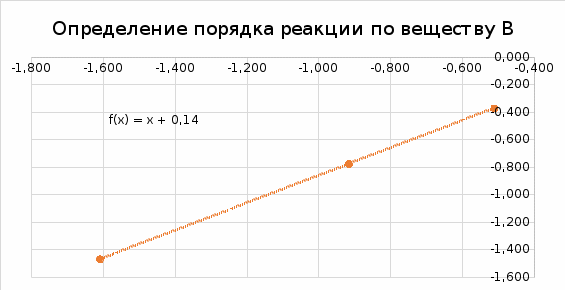 В последующих опытах (4 – 6) концентрация вещества B остается постоянной ([B]=[B]0), поэтому: lnk + m·ln[B]0 = D1. lnv = n ln[A] + D2. По результатам опытов (4-6) строим график зависимости lnv от ln[A] и найдем порядок реакции по веществу A. 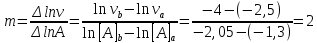 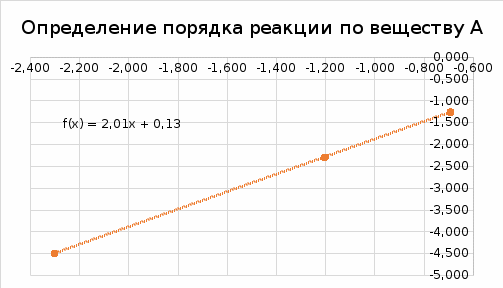 Таким образом, зависимость скорости от концентрации для исследуемой реакции v = k [A]2 [В] В этом уравнении порядок реакции по веществу В равен 1, порядок реакции по веществу A также равен 1. Сумма порядков по реагирующим веществам, равная 2, дает общий порядок реакции. Для определения константы скорости прологарифмируем дифференциальное кинетическое уравнение с учетом полученных порядков реакции по веществам А и В: lnk = lnv – 2ln[A] – ln[В]. Вычислив константу скорости для каждого опыта, найдем значение константы. 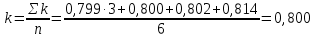
Таким образом, дифференциальное кинетическое уравнение имеет вид: v = 0,8 [A]2 [B] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
