математика. Определитель 1(2212)3(2213)4(2223) 9 Заменим 1й столбец матрицы а на вектор результата В

• Название: Определитель 1(2212)3(2213)4(2223) 9 Заменим 1й столбец матрицы а на вектор результата В
• Анкор: математика
• Дата: 29.12.2021
• Размер: 10.12 Kb.
• Имя файла: 2279844281.docx
• Тип: Документы; #321335

Запишем систему в виде: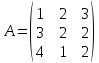



B^T = (3,1,3)

Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю.

Определитель:

∆ = 1∙(2∙2-1∙2)-3∙(2∙2-1∙3)+4∙(2∙2-2∙3) = -9

Заменим 1-й столбец матрицы А на вектор результата В.

3	2	3
1	2	2
3	1	2

Найдем определитель полученной матрицы.

∆₁ = (-1)¹⁺¹a₁₁∆₁₁ + (-1)²⁺¹a₂₁∆₂₁ + (-1)³⁺¹a₃₁∆₃₁ = 3∙(2∙2-1∙2)-1∙(2∙2-1∙3)+3∙(2∙2-2∙3) = -1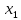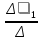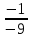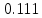



Заменим 2-й столбец матрицы А на вектор результата В.

1	3	3
3	1	2
4	3	2

Найдем определитель полученной матрицы.

∆₂ = (-1)¹⁺¹a₁₁∆₁₁ + (-1)²⁺¹a₂₁∆₂₁ + (-1)³⁺¹a₃₁∆₃₁ = 1∙(1∙2-3∙2)-3∙(3∙2-3∙3)+4∙(3∙2-1∙3) = 17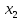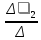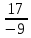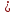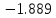



Заменим 3-й столбец матрицы А на вектор результата В.

1	2	3
3	2	1
4	1	3

Найдем определитель полученной матрицы.

∆₃ = (-1)¹⁺¹a₁₁∆₁₁ + (-1)²⁺¹a₂₁∆₂₁ + (-1)³⁺¹a₃₁∆₃₁ = 1∙(2∙3-1∙1)-3∙(2∙3-1∙3)+4∙(2∙1-2∙3) = -20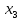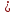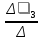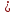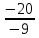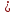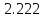



Выпишем отдельно найденные переменные Х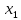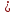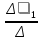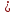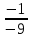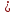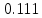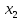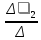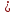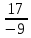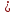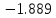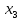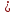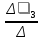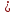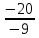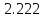







Проверка.

1∙0.111+2∙(-1.889)+3∙2.222 = 3

3∙0.111+2∙(-1.889)+2∙2.222 = 1

4∙0.111+1∙(-1.889)+2∙2.222 = 3
Решение было получено и оформлено с помощью сервиса:

Метод Крамера

Вместе с этой задачей решают также:

Решение методом Гаусса

Метод обратной матрицы

Матричный калькулятор

Умножение матриц онлайн

По координатам пирамиды найти: уравнение плоскостей, уравнение прямых, объем пирамиды

Производная онлайн