Оптимизация параметров многопроцессорной системы
 Скачать 1.54 Mb. Скачать 1.54 Mb.
|
 Московский автомобильно-дорожный государственный технический университет (МАДИ) Пояснительная записка к курсовой работе На тему: «Оптимизация параметров многопроцессорной системы» Вариант № 12 Выполнил: студент группы 3бИТС Устякин Д.А Проверил: к.т.н. Мезенцев К.Н. Москва 2021г. ОглавлениеВведение 3 1.Понятие системы массового обслуживания 4 2.Построение модели телефонных вызовов 19 2.1. Схема построения 20 2.2. Построение моделей в AnyLogic 20 2.3. Настройки элементов СМО 24 3. Анализ результатов моделирования 26 Заключение 29 Список литературы 30 ВведениеКурсовая работа состоит из теоретической и практической частей. В теоретической части рассмотрены системы массового обслуживания. Понятие системы массового обслуживания, структура системы массового обслуживания, дисциплины обслуживания и их характеристика. Системы массового обслуживания с приоритетным управлением: правила управления, определение параметров СМО. Правила построения систем массового обслуживания с потерями в AnyLogic. В практической части выполнено исследование схемы систем массового обслуживания с помощью построения модели движения заявок Моделирование выполнено с использованием программы AnyLogic8. Понятие системы массового обслуживанияПонятие системы массового обслуживания. При решении задач рациональной организации торговли, бытового обслуживания, складского хозяйства и т.п. достаточно полезна бывает интерпретация деятельности производственной структуры как системы массового обслуживания, т.е. системы, в которой, с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой - происходит постоянное удовлетворение этих запросов. Теория систем массового обслуживания. Система массового обслуживания (СМО) предполагает наличие следующих элементов: - входящий поток, - очередь, - обслуживающее устройство (каналы обслуживания), выходящий поток. Необходимо уяснить следующие термины: - требование – каждый отдельный запрос на выполнение какой-либо работы; - обслуживание – выполнение работы по удовлетворению поступившего требования; - обслуживающее устройство – объект, выполняющий обслуживание требований; - время обслуживания – период, в течение которого удовлетворяется требование на выполнение какой-либо работы; - время ожидания обслуживания – период от момента поступления требования до обслуживания. Классификация СМО: 1) По числу каналов обслуживания: - одноканальные, - многоканальные, 2) В зависимости от условий ожидания: - с потерями (отказами), - с ожиданием. 3) по дисциплине обслуживания: - с приоритетом, - без приоритета. 4) по характеру обслуживания: - однофазные, - многофазные. 5) по месту нахождения источника требования: - разомкнутые (источник требования находится вне СМО), - замкнутые. Теория системы управления запасами. Управление запасами заключается в установлении той или иной периодичности поставок, объемов, регулярности, сроков их выполнения. Совокупность правил, по которым принимаются решения по управлению запасами, называется системой (стратегией) управления запасами. В качестве параметров, по которым осуществляется управление запасами могут выступать: 1) размеры запасов – в системе с фиксированным размером заказов как только уровень запасов снижается до определенного критического уровня (точки заказа) происходит пополнение запасов до определенного уровня; время между заказами может быть разным); 2) периодичность заказа на пополнение запасов – в системе с фиксированной периодичностью заказа пополнение запасов осуществляется через одинаковые периоды (например, раз в неделю); при этом количество пополняемого запаса может быть разным. 3) поддерживаемый уровень запасов – в системе с двумя фиксированными уровнями уровнями (s, S – система) уровень запасов регламентируется как сверху, так и снизу; 4) саморегулирующиеся системы (изменяющийся размер заказа, периодичность и т.д.). Всякая СМО включает четыре элемента: входящий отток, очередь, обслуживающее устройство, выходящий поток. Требованием (клиентом, заявкой) в СМО называется каждый отдельный запрос на выполнение какой-либо работы. Обслуживание – это выполнение работы по удовлетворению поступившего требования. Объект, выполняющий обслуживание требований, называется обслуживающим устройством (прибором) или каналом обслуживания. Временем обслуживания называется период, в течение которого удовлетворяется требование на обслуживание, т.е. период от начало обслуживания и до его завершения. Период от момента поступления требования в систему и до начало обслуживания называется временем ожидания обслуживания. Время ожидания обслуживания в совокупности со временем обслуживания составляет время пребывания требования в системе. СМО классифицируются по разным признакам. 1. По числу каналов обслуживания СМО делятся на одноканальные и многоканальные. 2. В зависимости от условия ожидания требованием начала обслуживания различают СМО с потерями (отказами) и СМО с ожиданием. В СМО с потерями требования, поступившее в момент, когда все приборы заняты обслуживанием, получают отказ, они теряются для данной системы и никакого влияния на дальнейший процесс обслуживания не оказывают. Классическим примером системы с отказами является телефонная станция – требование на соединение получает отказ, если вызываемый абонент занят. Для системы с отказами основной характеристикой эффективности функционирования является вероятность отказа или средняя доля заявок, оставшихся необслуженными. В СМО с ожиданием требование, поступившее в момент, когда все приборы заняты обслуживанием, не покидает систему, а становится в очередь и ожидает, пока не освободится один из каналов. При освобождении очередного прибора одна из заявок, стоящих в очереди, немедленно принимается на обслуживание. Для СМО с ожиданием основными характеристиками являются математические ожидания длины очереди и времени ожидания. Примером системы с ожиданием может служить процесс восстановления работы телевизоров в ремонтной мастерской. Встречаются системы, лежащие между указанными двумя группами (смешанные СМО). Для них характерно наличие некоторых промежуточных условий: ограничениями могут быть ограничения во времени ожидания начала обслуживания, по длине очереди и т.п. В качестве характеристик эффективности может применяться вероятность отказа как в системах с потерями (или характеристики времени ожидания) и в системах с ожиданием. 3. По дисциплине обслуживания СМО делятся на системы с приоритетом в обслуживании и на системы без приоритета в обслуживании. Требования могут обслуживаться в порядке их поступления либо случайным образом, либо в зависимости от установленных приоритетов. 4. СМО могут быть однофазными и многофазными. В однофазных системах требования обслуживаются каналам одного типа (например, рабочими одной профессии) без передачи их от одного канала к другому, в многофазных системах такие передачи возможны. 5. По месту нахождения источника требования СМО делятся на разомкнутые (когда источник требования находится вне системы) и замкнутые (когда источник находится в самой системе). К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей которого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на наладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно. Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, портов и т.п. Для этих систем поступающий поток требований можно считать неограниченным. Методы и модели исследования СМО можно условно разбить на аналитические и статистические (имитационного моделирования процессов массового обслуживания). Аналитические методы позволяют получить характеристики системы как некоторые функции от параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффективность работы СМО. К сожалению, аналитическому решению поддается лишь довольно ограниченный круг задач теории массового обслуживания. Несмотря на постоянно ведущуюся разработку аналитических методов, во многих реальных случаях аналитическое решение либо невозможно получить, либо итоговые зависимости оказываются настолько сложными, что их анализ становится самостоятельной трудной задачей. Поэтому ради возможности применения аналитических методов решения приходится прибегать к различным упрощающим предположениям, что в некоторой степени компенсируется возможностью применения качественного анализа итоговых зависимостей (при этом, разумеется, необходимо, чтобы принятые допущения не искажали реальной картины процесса). В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач массового обслуживания, в которых поток требований является простейшим (пуассоновским). Под задачей управления товарными запасами понимается такая оптимизационная задача, в которой задана информация: · о поставках товара; · о спросе на товар; · об издержках и условиях хранения товарных запасов; · критерии оптимизации. В практической деятельности и служб маркетинга используются более простые принципиальные системы регулирования товарных запасов, основанные на различных стратегиях пополнения запасов, т.е. на определенных правилах этого пополнения, выраженных в достаточно общей форме. В качестве параметров в этих системах принимаются величина имеющихся на складе запасов, допустимые колебания уровня запасов, размеры заказа на пополнение запасов, его периодичность и др. Системы различаются между собой в зависимости от того, какие из параметров выбраны в качестве регулирующих. Принципиальные системы регулирования запасов, используемые в практике маркетинга, подробно описаны во многих учебниках и пособиях. Поэтому дадим здесь лишь краткий обзор этих систем. Система с фиксированным размером заказа. Это наиболее распространенная система, в которой размер заказа на пополнение запасов – постоянная величина, а поставка очередной партии товара осуществляется при уменьшении наличных запасов до определенного критического уровня, называемого точкой заказа. Поэтому регулирующими параметрами системы с фиксированным размером заказа являются: 1) точка заказа, т.е. фиксированный уровень запаса, при снижении до которого организуется заготовка очередной партии товара, и 2) размер заказа, т.е. величина партии поставки. Данную систему часто называют «двухбункерной», так как запас хранится как бы в двух бункерах: в первом бункере для удовлетворения спроса в течение периода между фактическим пополнением заказа, а во втором – для удовлетворения спроса в течение периода от момента подачи заказа до поступления очередной партии товара, т.е. во втором бункере хранится запас на уровне точки заказа. Система с фиксированной периодичностью заказа. При этой системе заказы на очередную поставку товарного запаса повторяются через равные промежутки времени. В конце каждого периода проверяется уровень запасов и исходя из этого определяется размер заказываемой партии; при этом запас пополняется каждый раз до определенного уровня, не превышающего максимальный запас. Таким образом, регулирующие параметры этой системы: 1) максимальный уровень запасов, до которого осуществляется их пополнение и 2) продолжительность периода повторения заказов. Система с фиксированной периодичностью заказа эффективна, когда имеется возможность пополнять запас в различных размерах, причем затраты на оформление заказа любого размера невелики. Одним из достоинств этой системы можно считать возможность периодической проверки остатков на складе и отсутствие необходимости вести систематический учет движения остатков. К недостаткам системы относится то, что она не исключает возможность нехватки товарных запасов. Система с двумя фиксированными уровнями запасов и с фиксированной периодичностью заказа. В этой системе допустимый уровень запасов регламентируется как сверху, так и снизу. Кроме максимального верхнего уровня запаса устанавливается нижний уровень (точка заказа). Если размер запаса снижается до нижнего уровня еще до наступления фиксированного времени пополнения запаса, то делается внеочередной заказ. В остальных случаях система с фиксированной периодичностью заказа. В данной системе имеется три регулирующих параметра: 1) максимальный уровень запаса, 2) нижний уровень запаса (точка заказа) и 3) длительность периода между заказами. Первые два параметра постоянны, третий – частично переменный. Рассматриваемая система сложнее предыдущей, однако, она позволяет исключить возможность нехватки товарного запаса. Недостатком системы является то, что пополнение запасов до максимального уровня не может производиться независимо от фактического расходования запасов. Модель динамики предполагает наличие параметров, наилучшим образом отражающих исходные данные. Реализация этого требования осуществляется с использованием метода наименьших квадратов (МНК), с которым студенты знакомы из курса математической статистики. Имитационное моделирование и исследование систем массового обслуживания. Имитационное моделирование" (ИМ) - двойной термин. "Имитация" и "моделирование" - синонимы. Фактически все области науки и техники являются моделями реальных процессов. Чтобы отличить математические модели друг от друга, исследователи стали давать им дополнительные названия. Термин "имитационное моделирование" означает, что мы имеем дело с такими математическими моделями, с помощью которых нельзя заранее вычислить или предсказать поведение системы, а для предсказания поведения системы необходим вычислительный эксперимент (имитация) на математической модели при заданных исходных данных. Основное достоинство ИМ: возможность описания поведения компонент (элементов) процессов или систем на высоком уровне детализации; отсутствие ограничений между параметрами ИМ и состоянием внешней среды РПС; возможность исследования динамики взаимодействия компонент во времени и пространстве параметров системы; Эти достоинства обеспечивают имитационному методу широкое распространение. Рекомендуется использовать имитационное моделирование в следующих случаях: Если не существует законченной постановки задачи исследования и идет процесс познания объекта моделирования. Имитационная модель служит средством изучения явления. Если аналитические методы имеются, но математические процессы сложны и трудоемки, и имитационное моделирование дает более простой способ решения задачи. Когда кроме оценки влияния параметров (переменных) процесса или системы желательно осуществить наблюдение за поведением компонент (элементов) процесса или системы (ПС) в течение определенного периода. Когда имитационное моделирование оказывается единственным способом исследования сложной системы из-за невозможности наблюдения явлений в реальных условиях (реакции термоядерного синтеза, исследования космического пространства). Когда необходимо контролировать протекание процессов или поведение систем путем замедления или ускорения явлений в ходе имитации. При подготовке специалистов для новой техники, когда на имитационных моделях обеспечивается возможность приобретения навыков в эксплуатации новой техники. Когда изучаются новые ситуации в РПС. В этом случае имитация служит для проверки новых стратегий и правил проведения натурных экспериментов. Когда особое значение имеет последовательность событий в проектируемых ПС и модель используется для предсказания узких мест в функционировании РПС. Однако ИМ наряду с достоинствами имеет и недостатки: Разработка хорошей ИМ часто обходится дороже создания аналитической модели и требует больших временных затрат. Может оказаться, что ИМ неточна (что бывает часто), и мы не в состоянии измерить степень этой неточности. Зачастую исследователи обращаются к ИМ, не представляя тех трудностей, с которыми они встретятся и совершают при этом ряд ошибок методологического характера. И тем не менее ИМ является одним из наиболее широко используемых методов при решении задач синтеза и анализа сложных процессов и систем. Одним из видов имитационного моделирования является статистическое имитационное моделирование, позволяющее воспроизводить на ЭВМ функционирование сложных случайных процессов. При исследовании сложных систем, подверженных случайным возмущениям используются вероятностные аналитические модели и вероятностные имитационные модели. В вероятностных аналитических моделях влияние случайных факторов учитывается с помощью задания вероятностных характеристик случайных процессов (законы распределения вероятностей, спектральные плотности или корреляционные функции). При этом построение вероятностных аналитических моделей представляет собой сложную вычислительную задачу. Поэтому вероятностное аналитическое моделирование используют для изучения сравнительно простых систем. Подмечено, что введение случайных возмущений в имитационные модели не вносит принципиальных усложнений, поэтому исследование сложных случайных процессов проводится в настоящее время, как правило, на имитационных моделях. В вероятностном имитационном моделировании оперируют не с характеристиками случайных процессов, а с конкретными случайными числовыми значениями параметров ПС. При этом результаты, полученные при воспроизведении на имитационной модели рассматриваемого процесса, являются случайными реализациями. Поэтому для нахождения объективных и устойчивых характеристик процесса требуется его многократное воспроизведение, с последующей статистической обработкой полученных данных. Именно поэтому исследование сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационного моделирования принято называть статистическим моделированием. Статистическая модель случайного процесса - это алгоритм, с помощью которого имитируют работу сложной системы, подверженной случайным возмущениям; имитируют взаимодействие элементов системы, носящих вероятностный характер. При реализации на ЭВМ статистического имитационного моделирования возникает задача получения на ЭВМ случайных числовых последовательностей с заданными вероятностными характеристиками. Численный метод, решающий задачу генерирования последовательности случайных чисел с заданными законами распределения, получил название "метод статистических испытаний" или "метод Монте-Карло". Так как метод Монте-Карло кроме статистического моделирования имеет приложение к ряду численных методов (взятие интегралов, решение уравнений), то целесообразно иметь различные термины. Итак, статистическое моделирование - способ изучения сложных процессов и систем, подверженных случайным возмущениям, с помощью имитационных моделей. Метод Монте-Карло - численный метод, моделирующий на ЭВМ псевдослучайные числовые последовательности с заданными вероятностными характеристиками. Методика статистического моделирования состоит из следующих этапов: Моделирование на ЭВМ псевдослучайных последовательностей с заданной корреляцией и законом распределения вероятностей (метод Монте-Карло), имитирующих на ЭВМ случайные значения параметров при каждом испытании; Преобразование полученных числовых последовательностей на имитационных математических моделях. Статистическая обработка результатов моделирования. Обобщенный алгоритм метода статистических испытаний представлен на рис. 1.1. 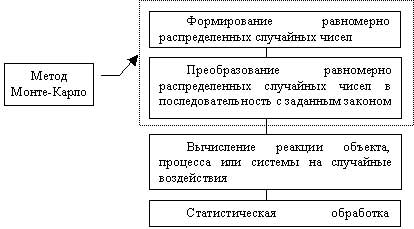 Рис. 1.1. Обобщенный алгоритм метода статистических испытаний Законы распределения времен в системе массового обслуживания: Пуассона, экспоненциальный, треугольный. Закон распределения Пуассона Распределение Пуассона - вероятностное распределение дискретного типа. Этот закон описывает закономерность появления случайных отказов в сложных системах и нашел широкое применение при определении вероятности появления и восстановления отказов. Случайная величина X распределена по закону Пуассона, если вероятность того, что эта величина примет определенное значение т, выражается формулой где Я - параметр распределения (Я = п • Р - среднее число появлений события в испытаниях или, иными словами, средняя плотность распределения точек (событий) на оси абсцисс); т — 0, 1, 2, 3, п - математическое ожидание Мх и дисперсия Dx случайной величины X для закона Пуассона равны параметру распределения X: Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Распределение Пуассона является однопараметрическим с параметром Я. На рис. 1.2 показано распределение Пуассона для значений параметра распределения: Я = 0,5, Я = 1,0, Я = 2иЯ = 3,5. 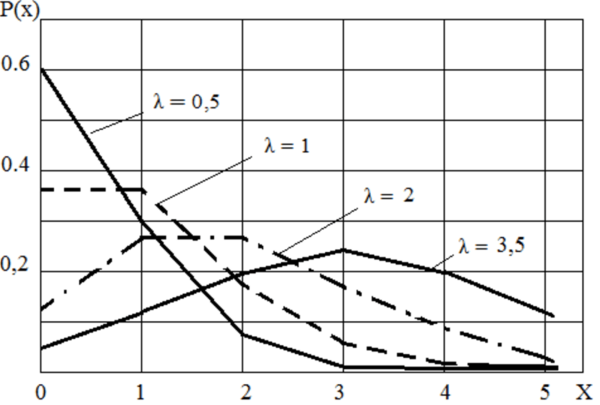 Рис. 1.2. Кривые распределения Пуассона (функция вероятности) Закон Пуассона используется тогда, когда необходимо определить вероятность того, что в системе за заданный период произойдет 1, 2, 3 отказа и т.д. Он моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона является предельным случаем биномиального распределения, когда вероятность Р осуществления события мала, но число испытаний п велико. Поэтому распределение Пуассона часто называют также «законом редких событий». С увеличением X распределение Пуассона стремится к нормальному распределению (распределению Гаусса) со среднеквадратичным отклонением Экспоненциальное распределение Экспоненциальный закон распределения, называемый также основным законом надежности, часто используют для прогнозирования надежности в период нормальной эксплуатации изделий, когда постепенные отказы еще не проявились и надежность характеризуется внезапными отказами. Эти отказы вызываются неблагоприятным стечением многих обстоятельств и поэтому имеют постоянную интенсивность. Экспоненциальное распределение позволяет моделировать интервалы времени между наступлением событий определенного рода. Оно находит довольно широкое применение, описывает распределение наработки на отказ сложных изделий, время безотказной работы элементов аппаратуры. Плотность распределения экспоненциального закона (рис. 10) описывается соотношением: функция распределения этого закона определяется соотношением функция надежности математическое ожидание случайной величины X дисперсия случайной величины X:  Рис. 1.3. Плотность распределения экспоненциального закона Параметр Я - положительная постоянная, называемая параметром экспоненциального распределения. Параметр Я оценивается на основе реальных данных. Экспоненциальный закон в теории надежности нашел широкое применение, так как он прост для практического использования. Почти все задачи, решаемые в теории надежности, при использовании экспоненциального закона оказываются намного проще, чем при использовании других законов распределения. Основная причина такого упрощения состоит в том, что при экспоненциальном законе вероятность безотказной работы зависит только от длительности интервала и не зависит от времени предшествующей работы. Экспоненциальный закон наиболее часто применяется в следующих случаях: - описание внезапных отказов; - описание времени безотказной работы в период после приработки и до появления постепенных отказов; - описание закона восстановления и описание продолжительности ремонтных работ; - описание времени безотказной работы системы с большим числом последовательно соединенных элементов и др. Например, для зубчатой передачи отказ может быть действием максимальной нагрузки на наиболее слабый зуб при его зацеплении; для элементов уплотнения аппаратуры, работающей под давлением - превышение допустимого давления. Треугольное распределение.
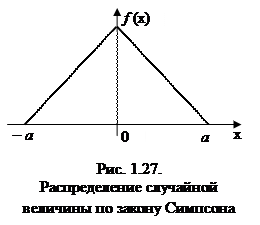
К распределению по закону Симпсона приводит сложение двух случайных величин, подчиненных закону равной вероятности при одинаковых параметрах рассеяния. Кривая рассеяния имеет вид равнобедренного треугольника (рис. 1.4), из-за чего закон Симпсона часто называют законом треугольника. При выборе в качестве начала отсчета случайной величины ее плотность распределения и математическое ожидание имеют следующий вид: 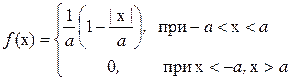 , (1.9) , (1.9)Mx = 0 , 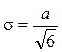 , , Построение модели телефонных вызововИнтенсивность потока телефонных звонков в агентство по заказу железнодорожных билетов, имеющему один телефон, составляет 16 вызовов в час. Продолжительность оформления заказа на билет равна 2.4 минуты. Определить относительную и абсолютную пропускную способность этой СМО и вероятность отказа (занятости телефона). Сколько телефонов должно быть в агентстве, чтобы относительная пропускная способность была не менее 0,75. 2.1. Схема построения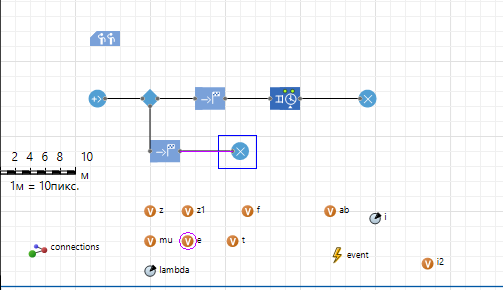 Рис. 2.1.1 - Схема процесса движения потока 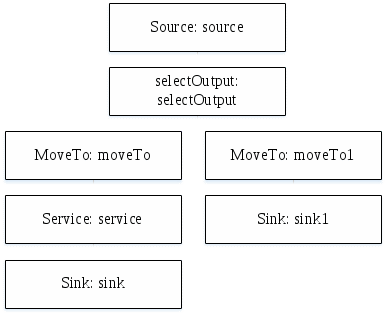 Рис. 2.1.2 – Объекты модели 2.2. Построение моделей в AnyLogicИсследование работы системы обслуживания проведем с помощью модели, структура которой показана в виде диаграммы компонентов UML. 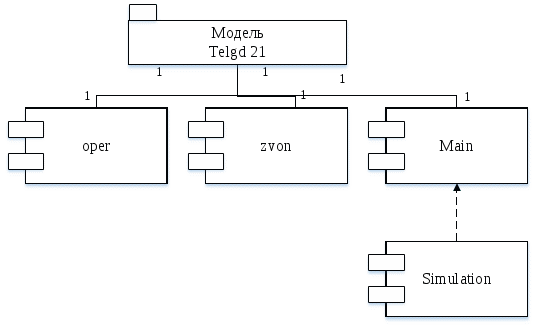 Рис. 2.2.1 - Модель для исследования систем обслуживания На рисунке 2.2.1 приняты следующие условные обозначения: Main – активный класс (агент) модели. oper – активный класс (агент) модели. zvon– активный класс (агент) модели. Simulation – компоненты «простой» эксперимент AnyLogic для тестирования созданных моделей Проведем моделирование в среде AnyLogic 8. Воспользуемся палитрой Enterprise Library и построим модель. Построенная модель приведена на рисунке 2.2.3 На рисунке 2.2.2 показана структура модели в виде диаграммы взаимодействия UML. Значения данных объектов модели приводятся в таблице 2.2.1 Таблица 2.2.1 - Объекты модели
 Рис.2.2.2 - Структура проекта 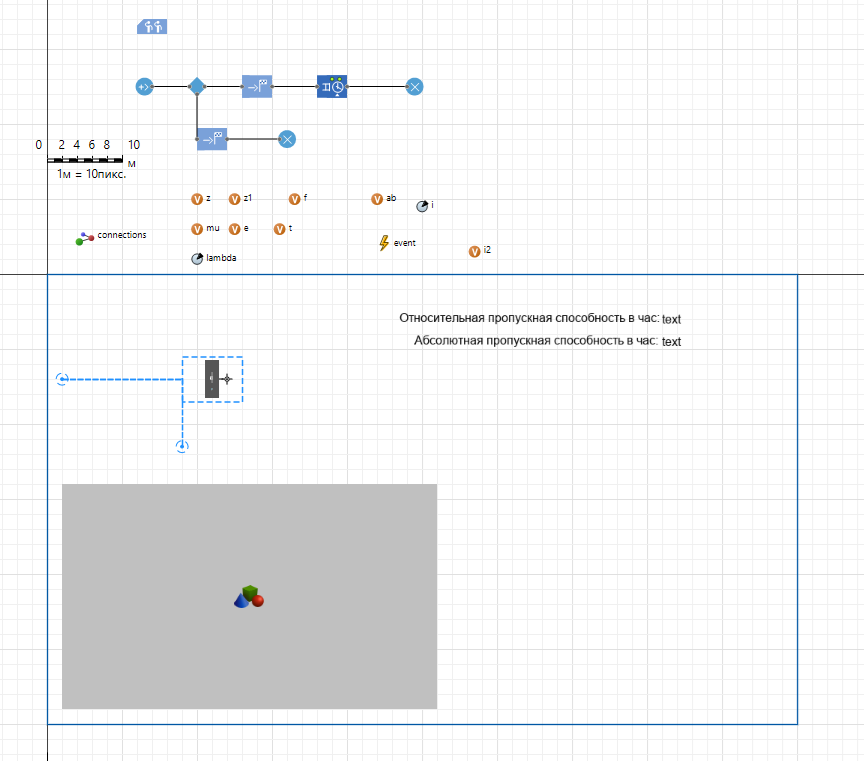 Рис.2.2.3 - Модель Чтобы данные гистограммы работали корректно, необходимо внести изменения в элементы: 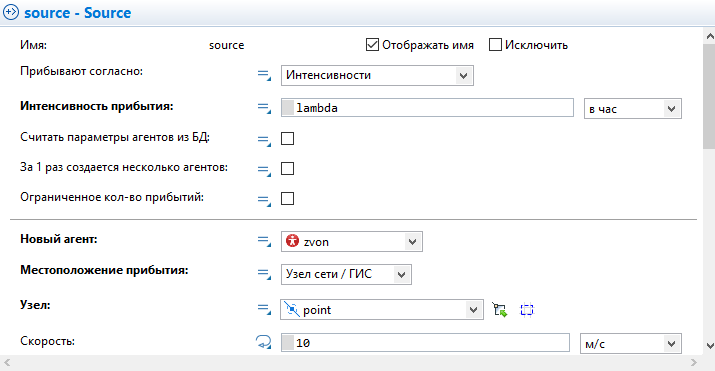 Рис. 2.2.4 - Настроенный элемент Source Рис. 2.2.4 - Настроенный элемент SourceПервым ползунком регулируется интенсивность потока телефонных звонков в агентство по заказу железнодорожных билетов. Вторым ползунком регулируется количество телефонов в агенстве. 2.3. Настройки элементов СМОЭлемент Source моделирует прибытие заявок с заданной интенсивностью. Для заявки – задается имя фигуры zvon. Местоположение прибытия: Узел сети/ГИС Узел: point Скорость: 10 Действие при выходе: t = time(HOUR); z++ Элемент service. имитирует процесс обслуживания заявки. Этот перечень задается в свойстве Тип ресурсов = resourcePool Количество ресурсов:1 Вместимость очереди: 1 Время задержки:2.4/i Место агентов queue: Node Место агентов Delay: path Элемент MoveTo. Используется для моделирования перемещения в сети. Задайте ему свойства: Имя = moveTo Тип Агента: zvon Место назначения: Узел сети/ГИС Узел: node Элемент MoveTo1. Используется для моделирования перемещения в сети. Задайте ему свойства: Имя = moveTo1 Тип Агента: zvon Место назначения: Узел сети/ГИС Узел = point1 Элемент resourcePool. Используется для формирования задания. Задайте ему свойства: Тип: Движущийся Тип Агента: oper Место назначения: Узел сети/ГИС Узел: node Скорость:10 Элемент selectOutput. используется для распределения заявок. Выход true выбирается: при выполнении условия Условие: service.size()<1 Элемент Sink используется для вывода заявки из сети. Действие при выходе: mu++ Элемент Sink1 используется для вывода заявки из сети. Действие при выходе: e++ 3. Анализ результатов моделированияМоделирование работы систем обслуживания проведем с экспериментом. Вариативный параметр: количество телефонов в агентстве. Структуру интерфейса экспериментов модели покажем с помощью диаграммы прецедентов UML (рисунок 3.1). 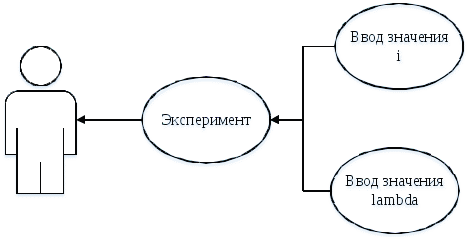 Рис. 3.1 – Прецеденты Опыт показывает (рис.3.2, рис.3.3, рис.3.4, рис.3.5). Сколько телефонов должно быть в агентстве, чтобы относительная пропускная способность была не менее 0,75. 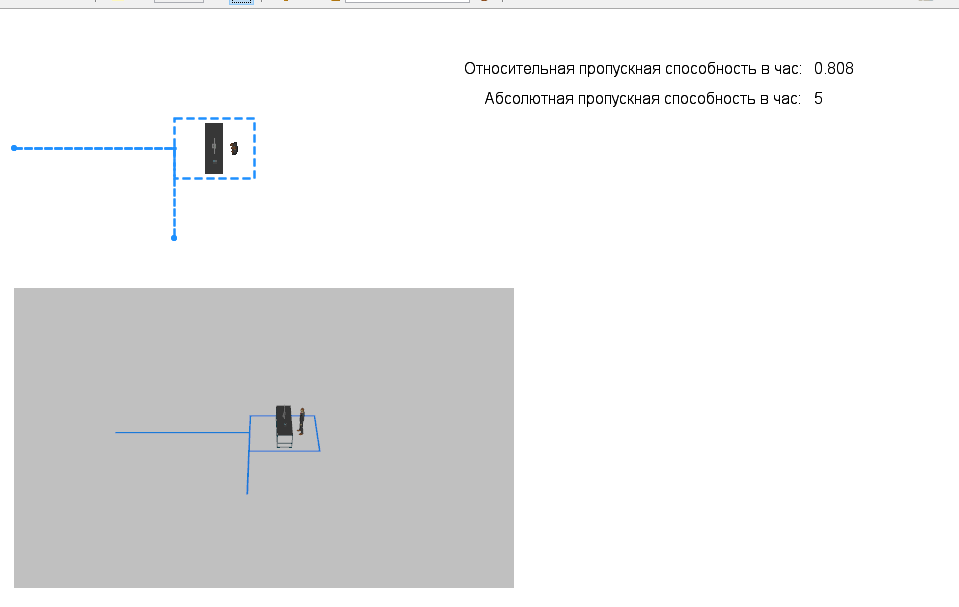 Рис.3.2 - Опыт при интенсивности 6, телефонов 1. 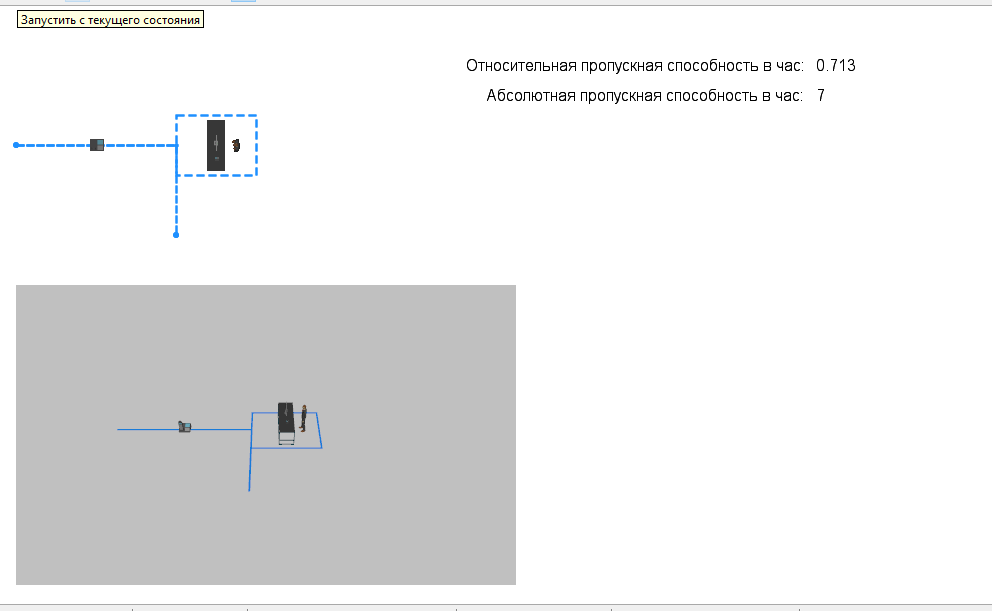 Рис.3.3 - Опыт при интенсивности 10, телефонов 1. 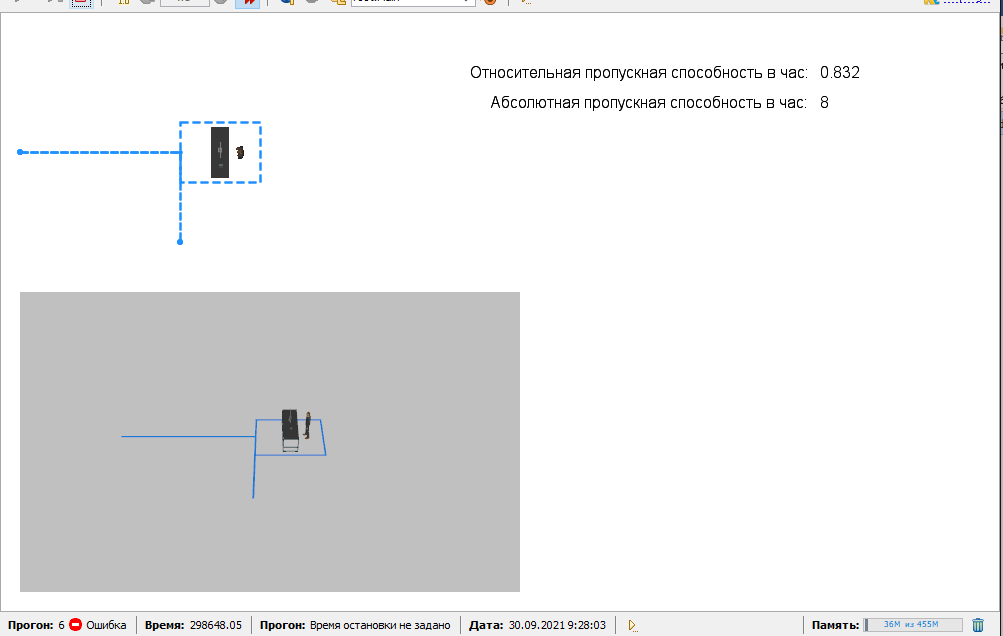 Рис.3.4 - Опыт при интенсивности 10, телефонов 2. 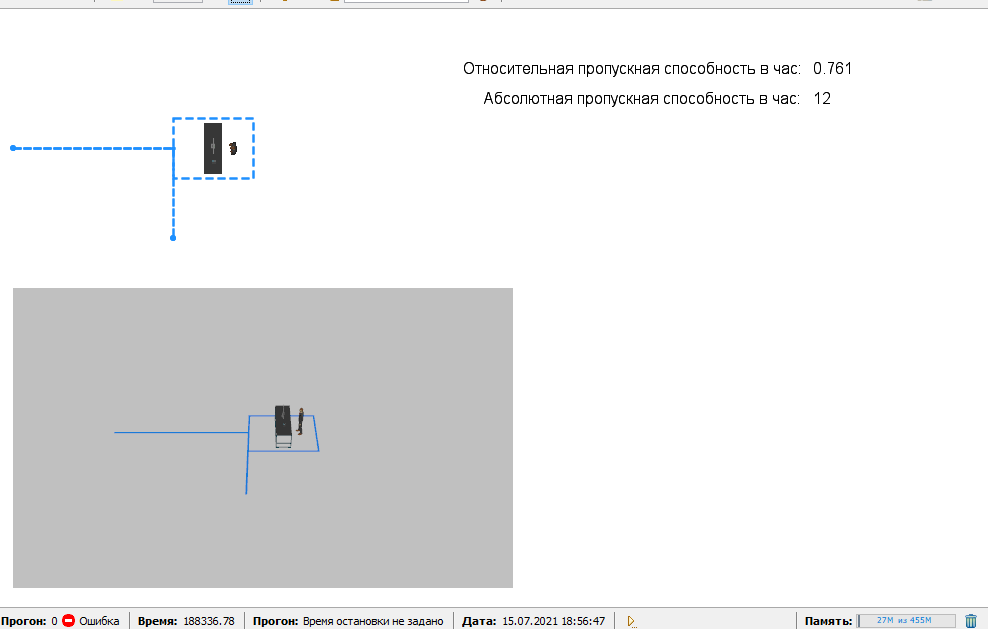 Рис.3.5 - Опыт при интенсивности 16, телефонов 2. Заключение В данной курсовой работе была разработана модель Системы Массового Обслуживания (СМО), благодаря которой возможен анализ потока телефонных звонков в агентство по заказу железнодорожных билетов. Входе эксперимента было выявлено что для обслуживания 16 вызовов в час достаточно 2 операторов. Список литературыРыжиков Ю.И. Имитационное моделирование. Теория и технологии. - СПб.: КОРОНА принт: М.: Альтекс-А, 2004. Варфоломеев В.И. Алгоритмическое моделирование элементов экономических систем: Практикум. Учеб. пособие. - М.: Финансы и статистика, 2000. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. - М.: Высшая школа, 1998. Самаров К.Л. Учебно-методическое пособие по разделу ЭЛЕМЕНТЫ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ Учеб. пособие для вузов. - М.: Резольвента, 2009 Советов Б.А., Яковлев С.А. Моделирование систем. М: Высшая школа, 1985. Вентцель Е.С. Исследование операций. М: Наука, 1980. |