план_МатЛаб - 2019. Организация занятий
 Скачать 50.67 Kb. Скачать 50.67 Kb.
|
|
План лабораторных работ по дисциплине «Введение в информационные технологии» \осень 2019 г. Организация занятий. Первые пять занятий вводные. Студенты выполняют одно общее задание, на примере которого преподаватель поясняет средства пакета МАТЛАБ.. Следующие занятия – выполнение индивидуальных однотипных заданий. Выполнение задания завершается отчётом, который студенты защищают, отвечая на контрольные вопросы. Рекомендуется выполнять задания дома и демонстрировать результаты в лаборатории. Для студентов доступна лицензионная версия. Форма отчетности – зачет с оценкой. Оценка зависит от числа и качества выполненных работ. Минимум для зачёта - 4 работы. Обязательные работы (на УДОВЛ.): 1+(3 или 4)+5+7. Для получения отличной оценки надо сделать все работы. Ориентировочный материал для вводных занятий. Занятие 1. Общие сведения о пакете. Среда MATLAB и ее конфигурирование. Основные элементы рабочей среды. Работа в Command Window . Контекстная помощь HELP и DEMOS. Окна Workspace и Current Directory. Арифметические операции, встроенные функции. Одномерные массивы и операции с ними. Сохранение, восстановление, удаление, изменение (окно Array Editor) переменных среды, точность представления данных. Занятие 2. Построение графиков функции одной переменной. Использование редактора текста для выполнения команд и создания скриптов. Определение собственной функции одной переменной. Команды построения и оформления графиков. Нотация ТЕХ для нанесения надписей. Занятие 3. Построение графиков функции двух переменных. Двухмерные массивы. Сечения массивов. Индексирование посредством массивов индексов. Построение сетки в декартовых и полярных координатах. Основные способы изображения поверхностей – каркасная, пленочная и контурная поверхности. Цветовые палитры и методы цветовой раскраски. Направление обзора. Управление камерой в редакторе графиков. Основные конструкция языка программирования – выражения, условные операторы, операторы циклов, внешние функции. Занятие 4. Приёмы численного решения задач алгебры и анализа. Функции пакета для решения следующих задач. Решение уравнений. Поиск экстремумов функции. Приближение табличных функций одной переменной. Операции с полиномами. Решение СЛАУ. Занятие 5. Символьные вычисления в МАТLAB, Понятие о символьных переменных. Решение следующих задач: алгебраические преобразования, поиск пределов, дифференцирование, разложение в ряд Тейлора, аналитическое решение уравнений, решение задач алгебры (векторы и матрицы 2-ого или 3-его порядков) Список работ, выполняемых самостоятельно. Даны две функции у(х) (файл task1_functions-2019. pdf) и полином Р3(х) (файл task1_poly-2019. pdf). Построить графики каждой функции в своих осях с нанесением характерных точек (корней, локальных экстремумов и точек перегиба (для полинома) – не более 3-х точек одного типа и не менее 2, если их несколько) Построить графики каждой функции (4 подграфика) без характерных точек, используя разные стили. На графике должны быть маркеры (не боле 10 и не менее 5) в выбранных точках Построить графики всех функций в одних осях (4 подграфика) без характерных точек и с характерными точками без подписей. Примечание Все графики должны содержать заголовки и подписи осей, подписи характерных точек с выносными линиями. Интервалы построения графиков выбирать с учётом ОДЗ. Графики функции одной переменной с разрывом и кусочно-заданной функции Для функции, построенной 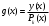 Построить график на интервале [x01, x02], содержащем корень полинома Рк(х) и нанести асимптоту в точке разрыва. Сделать «усечение» функции (изобразить только значения A < g(x) < B) по оси ординат по выбранным значениям А и В. Построить график "кусочно-заданной" функции, определённой на интервалах [x1. x2], [x2. x3], [x3. x4] как у(х), Рк(х), и g(x) соответственно (непрерывность функции не требуется). Подписать каждую часть графика, используя легенду. Каждая ветвь должна быть изображена своим стилем. Примечание Интервалы [x1. x2], [x2. x3], [x3. x4] подобрать так, чтобы значения функций не сильно отличались, но содержали некоторые характерные точки. Интервалы построения графиков выбирать с учётом ОДЗ. Все графики должны содержать заголовки и подписи осей, подписи характерных точек с выносными линиями. Для «усечения» не использовать функции axis, ylim и аналогичные Построение двух поверхностей второго порядка: Заданы две поверхности (файл task3_surf2oder-2019.pdf), а также коэффициенты 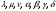 и смещения по осям и смещения по осям 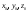 либо либо 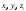 для их уравнений (см. далее). для их уравнений (см. далее). Построить графики каждой поверхности на отдельных осях (одна – каркасная, другая – плёночная, использовать разные цветовые палитры) Построить графики одной из поверхностей на 4 подграфиках (каркасная, плёночная – два варианта с разной закраской, топографическая - линиями уровней) задавая разные точки обзора. Построить графики другой поверхности, освещённой источником света на 4-х подграфиках, задав два разных положения источника и две точки обзора. Общее уравнение любой поверхности 2-ого порядка имеет вид: 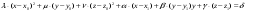 В зависимости от знаков и величины (ноль или нет) коэффициентов 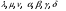 , различают следующие типы поверхностей (далее введены новые обозначения коэффициентов) , различают следующие типы поверхностей (далее введены новые обозначения коэффициентов)Эллипсоид 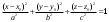 Параболоид эллиптический 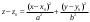 гиперболический 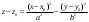 Гиперболоид однополостный 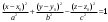 двуполостный 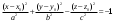 Цилиндр эллиптический 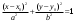 гиперболический 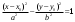 параболический 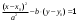 Конус 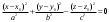 Построение взаимного расположения двух поверхностей второго порядка: Графически показать взаимное расположение и пересечение поверхностей, заданных в предыдущем пункте, выбрав три разных точки обзора. При необходимости, выбрать область построения каждой поверхности независимо так, чтобы обе поверхности были хорошо видны. Одна поверхность изображается как каркасная, другая как плёночная. использовать декартовы координаты использовать параметрическое задание поверхностей (цилиндрические или сферические координаты) Исследование свойств полиномов высокого порядка Для полинома, заданного коэффициентами (файл task5_polynom-2019.pdf):: построить график на интервале, содержащем все корни. построить графики на 2-х более узких интервалах (на выбор), где следует уточнить поведение функции. найти первые 3 производные и их вещественные корни. построить графики полинома и его производных на четырёх подграфиках друг под другом, обозначив на них точки, соответствующие вещественным корням Сравнить координаты точек экстремумов, вычисленных двумя способами: - используя функцию поиска минимума, - как корень производной. Внести случайное изменение, используя функцию rand, во второй коэффициент полинома (не более 5 %) и сравнить (вычислить относительную погрешность) каждого корня полинома Решение задач алгебры Для заданной системы линейных уравнений (файл task6_СЛАУ-2019.txt) получить решение тремя способами: По правилу Крамера С использованием обратной матрицы При помощи операции "\". Сравнить решения по значению максимальной компоненты вектора невязок Внести случайное изменение (в пределах 2%, 3%, 4%, 5 %) в правую часть системы, используя функцию rand, и построить график относительной погрешности решения, полученного с помощью операции "\", от относительной погрешности исходных данных. Решение задач средствами символьных вычислений Используя средства символьных преобразований пакета вычислить, упростить и представить в удобной форме, выражения для пределов, производных. В файле task7_analys-2019.pdf перечислены номера, а в архиве demidovich_1.rar– условия. Решить кубическое уравнение из задания 1 (файл task1_poly-2019.pdf) аналитически и вычислить корни, используя функцию VPA. Сравнить их с посчитанными численно (функциями roots и fzero). Разложить заданную функцию ( №-1 из файла task7_func-2019.jpg) в ряд Тейлора, удерживая разное число членов (2, 3, 4, 5). Вычислить коэффициенты полиномов и построить графики функции отрезка ряда Тейлора на симметричном ( относительно точки разложения) интервале, используя функцию plot. Используя функцию rand, построить систему линейных уравнений третьего порядка с целыми коэффициентами из интервала [ - 9, 9 ], имеющую единственное решение, Решить систему линейных уравнений аналитически, применяя функцию solve и обращая матрицу функцией inv. Удерживая 10 значащих цифр при помощи функции VPA , сравнить результаты с решением СЛАУ при помощи функции обратный слэш. Указания Не использовать функцию fplot. Не использовать встроенные функции МАТЛАБ для построения поверхностей второго порядка Не пользоваться средствами символьных вычислений при выполнении заданий 1-6. Доцент Смирнова Е.Н. |
