Тест 3 Теория пределов и Дифференциальное исчисление функции одн. Прототипы тестовых минимумов по дисциплинам Высшая математика Раздел Предел и непрерывность функции одной переменной. Дифференциальное исчисление функции одной переменной
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Прототипы тестовых «минимумов» по дисциплинам «Высшая математика» Раздел «Предел и непрерывность функции одной переменной. Дифференциальное исчисление функции одной переменной» Укажите определение предела функции  в точке в точке 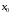 . .Варианты ответов (выбрать один верный ответ):  ; ; ; ; ; ; ; ;нет верного ответа. Укажите верные утверждения арифметики пределов. Варианты ответов (выбрать один или несколько верных ответов):  ; ;  ; ; ; ; ; ; ; ;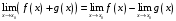 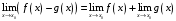 ; ;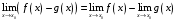  ; ; ; ; ; ;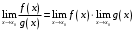 ; ;нет верного ответа. (в реальный вариант выбирается случайно 5 ответов) Укажите верные утверждения. Варианты ответов (выбрать один или несколько верных ответов): произведение бесконечно малой величины на постоянную величину есть величина бесконечно малая; произведение бесконечно малой величины на постоянную величину есть величина бесконечно большая; отношение бесконечно малой величины к постоянной величине есть величина бесконечно малая; отношение бесконечно малой величины к постоянной величине есть величина бесконечно большая; отношение постоянной величины к бесконечно малой величине к есть величина бесконечно малая; отношение постоянной величины к бесконечно малой величине к есть величина бесконечно большая; сумма двух бесконечно малых величин есть величина бесконечно малая; сумма двух бесконечно малых величин есть величина бесконечно большая; сумма двух бесконечно больших величин есть величина бесконечно малая; сумма двух бесконечно больших величин есть величина бесконечно нет верного ответа. разность двух бесконечно малых величин есть величина бесконечно малая; разность двух бесконечно малых величин есть величина бесконечно большая; разность двух бесконечно больших величин есть величина бесконечно малая; разность двух бесконечно больших величин есть величина бесконечно большая; нет верного ответа. (в реальный вариант выбирается случайно 5 ответов) Укажите формулы, которые носят название второго замечательного предела. Варианты ответов (выбрать один или несколько верных ответов):  ; ; ; ; ; ; ; ;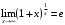 ; ; ; ;нет верного ответа. Укажите формулу, которая носит название первого замечательного предела. Варианты ответов (выбрать один или несколько верных ответов):  ; ; ; ; ; ; ; ;нет верного ответа. Укажите эквивалентные бесконечно малые. Варианты ответов (выбрать один или несколько верных ответов):  ; ; ; ;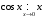 ; ; ; ; ; ; ; ; ; ;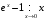 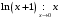 ; ; ; ;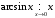 ; ; ; ; ; ;нет верного ответа. (в реальный вариант выбирается случайно 5 ответов) Пусть  и и  есть бесконечно малые функции при есть бесконечно малые функции при  , тогда если , тогда если  , то… , то…Варианты ответов (выбрать один верный ответ):  и и  являются эквивалентными бесконечно малыми; являются эквивалентными бесконечно малыми; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; и и  являются бесконечно малыми одного порядка малости; являются бесконечно малыми одного порядка малости;нет верного ответа. Пусть  и и  есть бесконечно малые функции при есть бесконечно малые функции при  , тогда если , тогда если  , то… , то…Варианты ответов (выбрать один верный ответ):  и и  являются эквивалентными бесконечно малыми; являются эквивалентными бесконечно малыми; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; и и  являются бесконечно малыми одного порядка малости; являются бесконечно малыми одного порядка малости;нет верного ответа. Пусть  и и  есть бесконечно малые функции при есть бесконечно малые функции при  , тогда если , тогда если 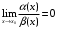 , то… , то…Варианты ответов (выбрать один верный ответ):  и и  являются эквивалентными бесконечно малыми; являются эквивалентными бесконечно малыми; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; и и  являются бесконечно малыми одного порядка малости; являются бесконечно малыми одного порядка малости;нет верного ответа. Пусть  и и  есть бесконечно малые функции при есть бесконечно малые функции при  , тогда если , тогда если  , то… , то…Варианты ответов (выбрать один верный ответ):  и и  являются эквивалентными бесконечно малыми; являются эквивалентными бесконечно малыми; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; и и  являются бесконечно малыми одного порядка малости; являются бесконечно малыми одного порядка малости;нет верного ответа. Пусть  и и  есть бесконечно малые функции при есть бесконечно малые функции при  , тогда если , тогда если  , то… , то…Варианты ответов (выбрать один верный ответ):  и и  являются эквивалентными бесконечно малыми; являются эквивалентными бесконечно малыми; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; является бесконечно малой более высокого порядка малости, чем является бесконечно малой более высокого порядка малости, чем  ; ; и и  являются бесконечно малыми одного порядка малости; являются бесконечно малыми одного порядка малости;нет верного ответа. Укажите условие, которое должно выполняться, чтобы по определению функция была непрерывна в некоторой точке. Варианты ответов (выбрать один верный ответ): существует предел функции в этой точке, и он равен значению функции в этой точке; оба односторонних предела функции в этой точке существуют и равны между собой; предел функции справа в этой точке существует и равен значению функции в этой точке; предел функции слева в этой точке существует и равен значению функции в этой точке; нет верного ответа. Укажите верное условие непрерывности функции в точке. Варианты ответов (выбрать один верный ответ): бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции; бесконечно малому приращению аргумента соответствует бесконечно большое приращение функции; бесконечно большому приращению аргумента соответствует бесконечно малое приращение функции; бесконечно большому приращению аргумента соответствует бесконечно большое приращение функции; нет верного ответа. Укажите условия, которые должны одновременно выполняться, чтобы функция  была непрерывной в точке была непрерывной в точке 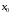 . .Варианты ответов (выбрать один или несколько верных ответов): 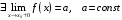 ; ; ; ; ; ;нет верного ответа. Укажите условие, при выполнении которого точка 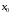 для функции для функции  являлась точкой разрыва первого рода (точкой устранимого разрыва). являлась точкой разрыва первого рода (точкой устранимого разрыва).Варианты ответов (выбрать один или несколько верных ответов):  ; ;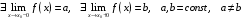 ; ;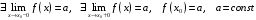 ; ; ; ; ; ;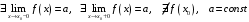 . .нет верного ответа. Укажите условие, при выполнении которого точка 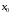 для функции для функции  являлась точкой разрыва первого рода (точкой скачка). являлась точкой разрыва первого рода (точкой скачка).Варианты ответов (выбрать один или несколько верных ответов):  ; ;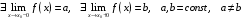 ; ;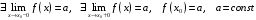 ; ; ; ; ; ;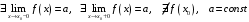 . .нет верного ответа. Укажите условие, при выполнении которого точка 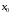 для функции для функции  являлась точкой разрыва второго рода (точкой бесконечного разрыва). являлась точкой разрыва второго рода (точкой бесконечного разрыва).Варианты ответов (выбрать один или несколько верных ответов):  ; ;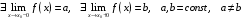 ; ;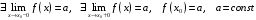 ; ; ; ; ; ;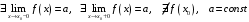 . .нет верного ответа. Что называется производной функции в точке? Варианты ответов (выбрать один верный ответ): предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю; предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к бесконечности; предел отношения приращения аргумента к приращению функции, когда приращение аргумента стремится к нулю; предел отношения приращения аргумента к приращению функции, когда приращение аргумента стремится к бесконечности; нет верного ответа. Укажите верное определение производной функции  в точке в точке 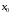 . .Варианты ответов (выбрать один верный ответ): 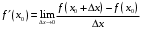 ; ; ; ; ; ; ; ;нет верного ответа. |
