Тест 3 Теория пределов и Дифференциальное исчисление функции одн. Прототипы тестовых минимумов по дисциплинам Высшая математика Раздел Предел и непрерывность функции одной переменной. Дифференциальное исчисление функции одной переменной
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
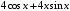 ; ;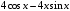 нет верного ответа. Найти 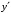 , если , если 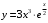 . .Варианты ответов (выбрать один верный ответ): 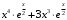 ; ;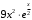 ; ;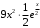 ; ;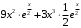 ; ;нет верного ответа. Найти 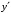 , если , если 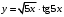 . .Варианты ответов (выбрать один верный ответ): 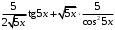 ; ;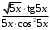 ; ;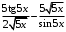 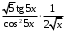 ; ;нет верного ответа. Найти 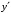 , если , если 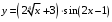 . .Варианты ответов (выбрать один верный ответ): 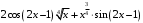 ; ;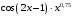 ; ;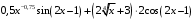 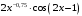 ; ;нет верного ответа. Найти 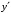 , если , если 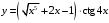 . .Варианты ответов (выбрать один верный ответ): 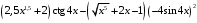 ; ;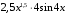 ; ;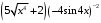 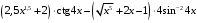 ; ;нет верного ответа. Найти значение производной функции 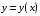 : : 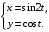 в точке, соответствующей значению параметра в точке, соответствующей значению параметра 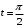 . .Ответ (задание с числовым ответом):____. Найти уравнение касательной к графику функции 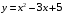 в точке c абсциссой в точке c абсциссой 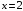 . .Варианты ответов (выбрать один верный ответ): 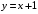 ; ;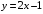 ; ;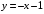 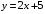 ; ;нет верного ответа. Найти уравнение нормали к графику функции 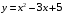 в точке c абсциссой в точке c абсциссой 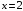 . .Варианты ответов (выбрать один верный ответ): 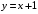 ; ;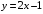 ; ;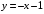 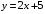 ; ;нет верного ответа. Найти промежутки выпуклости функции 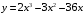 . .Варианты ответов (выбрать один верный ответ): 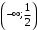 ; ;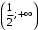 ; ;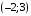 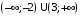 ; ;нет верного ответа. Найти промежутки вогнутости функции 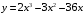 . .Варианты ответов (выбрать один верный ответ): 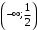 ; ;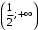 ; ;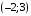 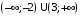 ; ;нет верного ответа. Найти точку минимума функции  , если , если 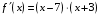 . .Если у функции нет точки минимума, в ответе указать: -1000. Ответ (задание с числовым ответом):____. Найти точку максимума функции  , если , если 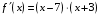 . .Если у функции нет точки минимума, в ответе указать: -1000. Ответ (задание с числовым ответом):____. Указать точки экстремума 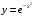 . .Варианты ответов (выбрать один или несколько верных ответов): 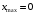 ; ;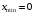 ; ;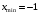 ; ;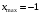 ; ;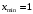 ; ;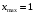 ; ;нет верного ответа. Указать точку максимума функции 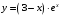 . .Варианты ответов (выбрать один верный ответ): 2; 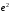 ; ;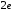 ; ;0; нет верного ответа. Указать точку минимума функции 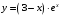 . .Варианты ответов (выбрать один верный ответ): 2; 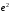 ; ;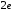 ; ;0; нет верного ответа. |
