Тест 3 Теория пределов и Дифференциальное исчисление функции одн. Прототипы тестовых минимумов по дисциплинам Высшая математика Раздел Предел и непрерывность функции одной переменной. Дифференциальное исчисление функции одной переменной
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
|
Что называется дифференциалом функции? Варианты ответов (выбрать один верный ответ): главная линейная относительно приращения аргумента часть приращения функции; производная этой функции, если она существует; производная этой функции, умноженная на некоторую бесконечно малую; предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю; нет верного ответа. Укажите геометрический смысл производной функции  в точке в точке 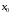 . .Варианты ответов (выбрать один верный ответ): тангенс угла наклона касательной, проведенной в точке с абсциссой 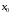 к графику функции к графику функции  , к положительному направлению оси абсцисс; , к положительному направлению оси абсцисс;угол наклона касательной, проведенной в точке с 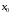 к графику функции к графику функции  , к положительному направлению оси абсцисс; , к положительному направлению оси абсцисс;угол наклона нормали, проведенной в точке с абсциссой 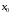 к графику функции к графику функции  , к положительному направлению оси абсцисс; , к положительному направлению оси абсцисс;угол наклона касательной, проведенной в точке с абсциссой 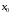 к графику функции к графику функции  , к положительному направлению оси ординат; , к положительному направлению оси ординат;нет верного ответа. Каков физический смысл производной некоторой функции в некоторой точке, если функция описывает некоторый процесс? Варианты ответов (выбрать один верный ответ): мгновенная скорость протекания этого процесса; мгновенное ускорение протекания этого процесса; непрерывность протекания процесса; связность протекания процесса; нет верного ответа. Каков геометрический смысл дифференциала функции в точке? Варианты ответов (выбрать один верный ответ): приращение ординаты касательной к графику функции в этой точке, когда переменная икс получает соответствующее приращение; отношение приращения функции к приращению аргумента; приращение функции, когда переменная х получает некоторое приращение; тангенс угла наклона касательной, проведенной в этой точке к графику этой функции, к положительному направлению оси абсцисс; нет верного ответа. Укажите уравнение касательной к графику функции  , проведенной в точке , проведенной в точке 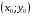 . .Варианты ответов (выбрать один верный ответ): 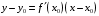 ; ;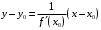 ; ;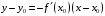 ; ;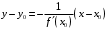 ; ;нет верного ответа. Укажите уравнение нормали к графику функции  , проведенной в точке , проведенной в точке 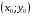 . .Варианты ответов (выбрать один верный ответ): 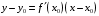 ; ;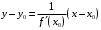 ; ;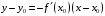 ; ;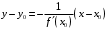 ; ;нет верного ответа. Какую прямую задает уравнение 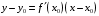 для графика непрерывной и дифференцируемой функции для графика непрерывной и дифференцируемой функции  в точке в точке  ? ?Варианты ответов (выбрать один верный ответ): касательную; секущую; нормаль; эволюту; нет верного ответа. Какую прямую задает уравнение  для графика непрерывной и дифференцируемой функции для графика непрерывной и дифференцируемой функции  в точке в точке  ? ?Варианты ответов (выбрать один верный ответ): касательную; секущую; нормаль; эволюту; нет верного ответа. Укажите верные правила дифференцирования, где  , , 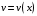 , , 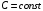 . .Варианты ответов (выбрать один или несколько верных ответов): 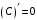 ; ;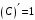 ; ;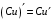 ; ;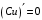 ; ;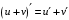 ; ;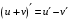 ; ;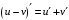 ; ;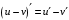 ; ;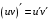 ; ;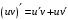 ; ;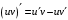 ; ;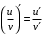 ; ;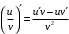 ; ;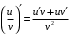 ; ;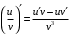 ; ;нет верного ответа. (в реальный вариант выбирается случайно 5 ответов) Укажите верные формулы таблицы производных. Варианты ответов (выбрать один или несколько верных ответов): 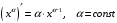 ; ;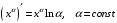 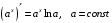 ; ;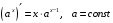 ; ;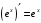 ; ;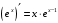 ; ;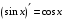 ; ;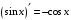 ; ;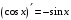 ; ;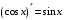 ; ;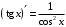 ; ;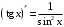 ; ;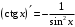 ; ;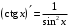 ; ;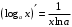 ; ;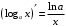 ; ;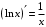 ; ;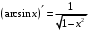 ; ;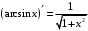 ; ;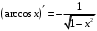 ; ;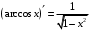 ; ;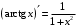 ; ;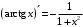 ; ;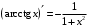 ; ;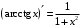 ; ;нет верного ответа. (в реальный вариант выбирается случайно 5 ответов) Укажите верные формулы дифференцирования функции  , заданной параметрически: , заданной параметрически: 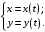 Варианты ответов (выбрать один или несколько верных ответов): 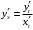 ; ;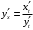 ; ;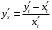 ; ;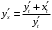 ; ;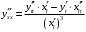 ; ;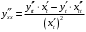 ; ;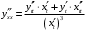 ; ;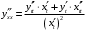 ; ;нет верного ответа. (в реальный вариант выбирается случайно 5 ответов) Укажите верную приближенную формулу. Варианты ответов (выбрать один верный ответ): 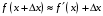 ; ;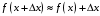 ; ;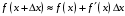 ; ;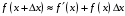 ; ;нет верного ответа. Укажите не верные применения правила Лопиталя в случае существования второго предела в формулах: Варианты ответов (выбрать один или несколько верных ответов): 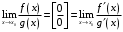 ; ;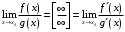 ; ;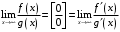 ; ;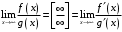 ; ;нет верного ответа. Укажите необходимое условие убывания функции  в точке в точке 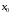 . .Варианты ответов (выбрать один верный ответ):  ; ; ; ; ; ; ; ;нет верного ответа. Укажите необходимое условие возрастания функции  в точке в точке 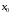 . .Варианты ответов (выбрать один верный ответ): 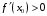 ; ;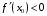 ; ;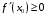 ; ; ; ;нет верного ответа. Укажите достаточное условие убывания функции  в точке в точке  . .Варианты ответов (выбрать один верный ответ):  ; ; ; ; ; ; ; ;нет верного ответа. Укажите достаточное условие возрастания функции  в точке в точке  . .Варианты ответов (выбрать один верный ответ):  ; ;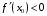 ; ;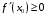 ; ;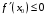 ; ;нет верного ответа. Укажите необходимое условие точки экстремума функции. Варианты ответов (выбрать один верный ответ): производная функции в этой точке равняется нулю или не существует; производная функции в этой точке равняется нулю; производная функции в этой точке равняется не существует; производная второго порядка функции в этой точке равняется нулю; нет верного ответа. Укажите достаточные условия точки экстремума функции. Варианты ответов (выбрать один или несколько верных ответов): производная функции при переходе через эту точку меняет свой знак, а в самой точке равняется нулю; производная первого порядка функции в этой точке равна нулю, а производная второго порядка отлична от нуля; производная функции в этой точке равна нулю или не существует; производная функции второго порядка в этой точке равна нулю или не существует; нет верного ответа. Укажите достаточное условие выпуклости графика функции  в точке в точке 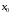 . .Варианты ответов (выбрать один верный ответ): 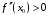 ; ;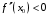 ; ;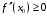 ; ;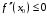 ; ;нет верного ответа. Укажите достаточное условие вогнутости графика функции  в точке в точке 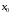 . .Варианты ответов (выбрать один верный ответ): 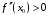 ; ;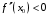 ; ;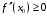 ; ;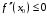 ; ;нет верного ответа. Укажите достаточные условия точки перегиба функции в точке. Варианты ответов (выбрать один или несколько верных ответов): вторая производная функции при переходе через эту точку меняет свой знак с плюса на минус; вторая производная функции в этой точке равна нулю; вторая производная в этой точке не существует; вторая производная функции при переходе через эту точку меняет свой знак с минуса на плюс; нет верного ответа. Укажите условия, при которых прямая 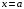 будет являться вертикальной асимптотой к графику функции будет являться вертикальной асимптотой к графику функции  . . Варианты ответов (выбрать один или несколько верных ответов): 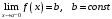 ; ;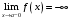 ; ;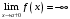 ; ;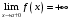 ; ;нет верного ответа. Укажите верные формулы нахождения коэффициентов, при которых прямая 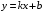 будет являться наклонной (горизонтальной) асимптотой графика функции будет являться наклонной (горизонтальной) асимптотой графика функции  . .Варианты ответов (выбрать один или несколько верных ответов): 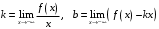 ; ;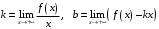 ; ; |
