ПАМЯТКА
по теме «Физический и геометрический смыслы производной. Уравнение касательной к графику функции»
Физический смысл производной.
S(t)- расстояние (функция от времени), v(t) – скорость, a(t) - ускорение
Производная от расстояния есть скорость точки: 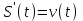
Производная от скорости есть ускорение: 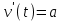 (t) (t)
Г еометрический смысл производной. еометрический смысл производной.
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке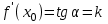
Если угол наклона между положительным направлением оси ОХ и касательной, проведённой к графику функции в заданной точке:
острый, то производная положительная;
тупой, то производная отрицательная;
равен нулю, то производная в этой точке равна нулю.
Уравнение касательной к графику функции y=f(x) в точке x0 : 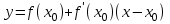
Алгоритм нахождения уравнения касательной:
вычислить 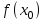
вычислить 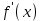
вычислить 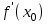
найденные значения подставить в уравнение касательной
Формула Лагранжа 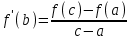 , где bϵ (a,c) , где bϵ (a,c)
|
ПАМЯТКА
по теме «Физический и геометрический смыслы производной. Уравнение касательной к графику функции»
Физический смысл производной.
S(t)- расстояние (функция от времени), v(t) – скорость, a(t) - ускорение
Производная от расстояния есть скорость точки: 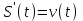
Производная от скорости есть ускорение: 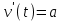 (t) (t)
Г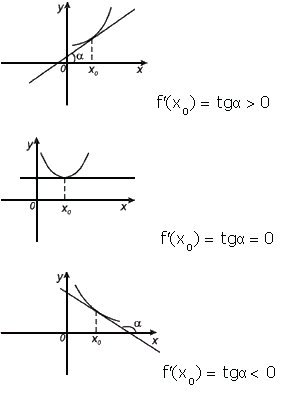 еометрический смысл производной. еометрический смысл производной.
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке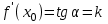
Если угол наклона между положительным направлением оси ОХ и касательной, проведённой к графику функции в заданной точке:
острый, то производная положительная;
тупой, то производная отрицательная;
равен нулю, то производная в этой точке равна нулю.
Уравнение касательной к графику функции y=f(x) в точке x0 : 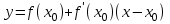
Алгоритм нахождения уравнения касательной:
вычислить 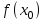
вычислить 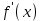
вычислить 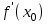
найденные значения подставить в уравнение касательной
Формула Лагранжа 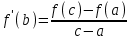 , где bϵ (a,c) , где bϵ (a,c)
|
 Скачать 37.13 Kb.
Скачать 37.13 Kb.