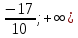Внимание! Данное задание необходимо выполнить и отправить на проверку преподавателю. Задание
 Скачать 12.79 Kb. Скачать 12.79 Kb.
|
|
Внимание! Данное задание необходимо выполнить и отправить на проверку преподавателю. Задание. Для функции 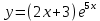 Найти область определения, точки разрыва. Разделить функцию на части, чтобы найти О.О. для каждой части : 2х+3 / 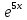 / 5х / 5хО.О для 2х+3, является х  R / О.О для R / О.О для 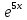 , является х , является х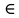 R/ О.О для 5х является х R/ О.О для 5х является х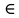 R RНайти пересечение = х∈R Исследовать функцию на четность, периодичность. f= 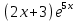 , подставить х=-х, f=(-х)=(2х(-х)+3) , подставить х=-х, f=(-х)=(2х(-х)+3)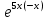 , f(-x)=(-2х+3) , f(-x)=(-2х+3)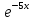 , поскольку ни f(-x)=f(x), ни f(-x)=-f(x) не выполнены , функция не четная, ни нечетная , поскольку ни f(-x)=f(x), ни f(-x)=-f(x) не выполнены , функция не четная, ни нечетнаяИсследовать поведение функции на концах области определения. Указать асимптоты. limx→-∞2x+3e5x=0 limx→+∞2x+3e5x=limx→+∞2x+31e5x=+∞0=+∞; Функция определена всюду, следовательно, вертикальных асимптот нет Найти наклонные асимптоты y=kx+b , limx→-∞fxx=limx→-∞2x+3e5xx=0; y=0- горизонтальная (наклонная) асимптота Найти промежутки монотонности. Точки экстремума. 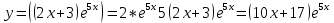 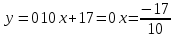
При 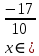 ;+ ;+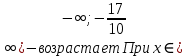 ) – убывает ) – убывает Х= 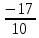 точка минимума точка минимума При переходе через критическую точку x=-1,7 производная меняет знак c минуса на плюс. Следовательно, в точке K-1,7;0 функция имеет минимум. Найти промежутки выпуклости. Точки перегиба. y``=((10x+17) 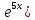 `=10 `=10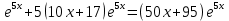 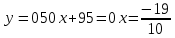 Найдем интервалы выпуклости и вогнутости функции. Вторая производная. f''(x) = 5·(10·x+17)·e5·x+10·e5·x или f''(x) = (50·x+95)·e5·x Находим корни уравнения. Для этого полученную функцию приравняем к нулю. (50·x+95)·e5·x = 0 Откуда точки перегиба: x1 = -19/10
6. Найти площадь фигуры, ограниченной графиком функции и прямыми 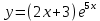 𝑥 = 0, 𝑥 = 2, 𝑦 = 0. 𝑥 = 0, 𝑥 = 2, 𝑦 = 0.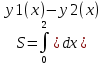 S=2.907* S=2.907*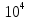 Результаты исследования оформить в виде таблицы.
|

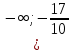 )
)