Орындаан Трсынбаев Болатбек Нса 13 Тобы

• Название: Орындаан Трсынбаев Болатбек Нса 13 Тобы
• Анкор: labka
• Дата: 01.12.2022
• Размер: 265.73 Kb.
• Имя файла: 4labMATLAB.docx
• Тип: Документы; #823472

ҚАЗАҚСТАН РЕСПУБЛИКАСЫ ҒЫЛЫМ ЖӘНЕ ЖОҒАРЫ БІЛІМ МИНИСТРЛІГІ


Коммерциялық емес акционерлік қоғам

«Ғ. Ж. ДӘУКЕЕВ атындағы

АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ»


Мамандығы: Интеграция и управление Smart технологиями


Орындаған: Тұрсынбаев Болатбек
Нұсқа : 13
Тобы: ИУТЭк-21-2
Тексерген: Даримбаева Н

Алматы, 2022

Зертханалық жұмыс №4 Автоматты реттеу жүйесінің қарапайым сызықты емес сипаттамаларын зерттеу

Жұмыстың мақсаты: қарапайым сызықты емес буындармен танысу және олардың сипаттамаларын зерттеу

1. Қысқаша теориялық кіріспе

Автоматты реттеудің сызықты емес (бейсызық) жүйелері деп ең болмағанда бір буыны сызықты емес теңдеумен сипатталатын жүйені айтады. Мұндай буындар сызықты емес буындар немесе сызықты емес элементтер деп аталады.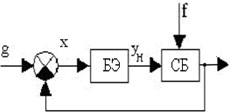

Сызықты емес жүйелерді эквивалентті түрлендіру жолымен бейсызық (сызықты емес) элемент пен сызықты бөлікті тізбектей қосатын тұйықталған контур түрінде қарастырамыз. Сызықты емес жүйенің сқлбасы 6.1 суретте көрсетілген.

БЭ – бейсызық элемент; СБ – сызықты бөлік.

1. 
   сурет – Сызықты емес жүйе сұлбасы
   

Сызықты емес жүйелердің көп бөлігі сызықталуға келеді және типтік динамикалық буындармен сипатталады.

Сызықты емес буындардың түрлері:

• 
  бір белгілі сипаттамаларынан тұратын сызықты емес буын (статикалық бейсызықтылық);
  
• 
  көп белгілі сипаттамаларынан тұратын сызықты емес буын (динамикалық бейсызықтылық);
  
• 
  ерекше сызықты емес элементтері.
  

Буынның бір белгілі сипаттамасы кіріс координаталарының мәніне ғана сезімталдығы болады, буын кіріс координатасының қозғалыс бағытына не оның туындысына сезімталдығы болмайды.

Сызықты емес буындардың түрлері:

Тегісқисықсызықтысипаттамалысызықтыемесбуындар.

Бұл сипаттамалар 6.2 суретте көрсетілген.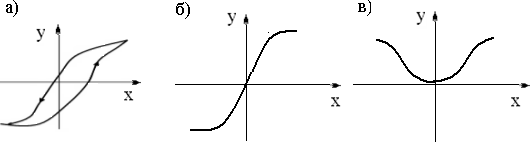

а – гистерезис тәрізді; б, в - күшейткішті.

2. 
   сурет - Тегіс қисықсызықты сипаттамалар
   

2. 
   , а - суретте екі белгілі гистеризис тәрізді (кешігуші) сипаттама көрсетілген. 6.1, б - суретте қанығу аймағынан тұратын немесе шектеу және нақты қуат күшейткішіне сәйкес келетін сипаттама, ал 6.1, в - нақты қуат күшейткішін көрсететін сипаттама көрсетілген. 6.1, а және б - суреттердегі сипаттама жұпсыз-симметриялы, ал 6.1, в - суретте жұп-симметриялы түрі көрсетілген.
   

1. 
   кесте – Қанығу аймағынан тұратын бесызықты блоктардың параметрлері
   

   Қанығу аймағының сипаттамасы	Нұсқалар	b параметрі	Сезімталдығы жоқ аймақтың сипаттамасы	Нұсқалар	b параметрі
   	1	0,7		1	2,3
   	2	1,3		2	1,7
   	3	2,8		3	0,3
   	4	3,5		4	4,8
   	5	4,2		5	3,4
   	6	5,6		6	5,6
   	7	6,9		7	2,1
   	8	1,7		8	6,9
   	9	2,3		9	3,5
   	10	0,9		10	5,4
   	11	3,7		11	2,8
   	12	5,2		12	6,9
   	13	3,3		13	2,3
   	14	2,7		14	1,9
   	15	1,3		15	2,3
   	16	4,9		16	5,8
   	17	3,6		17	2,4
   	18	5,8		18	5,6
   	19	2,3		19	2,1
   	20	5.9		20	3,9

2. 
   кесте – Гестирезисті бейсызықты блоктардың параметрлері
   

Гистерезисті сипаттама	Нұсқалар	a параметрі	b параметрі
	1	2	0,7
	2	1,1	1,4
	3	2	2,8
	4	0,5	0,9
	5	3,3	3,7
	6	0,9	1,5
	7	3,7	4,3
	8	2,2	2,6
	9	1,5	3,1
	10	4,8	3,7
	11	8,9	2,5
	12	5,3	1,3
	13	1,5	3,7
	14	4,3	2,2
	15	2,6	1,5
	16	3,1	4,8
	17	3,7	8,9
	18	2,5	5,3
	19	1,3	1.8
	20	2.4	3.5

1. 
   Қанығу буыны(Saturation)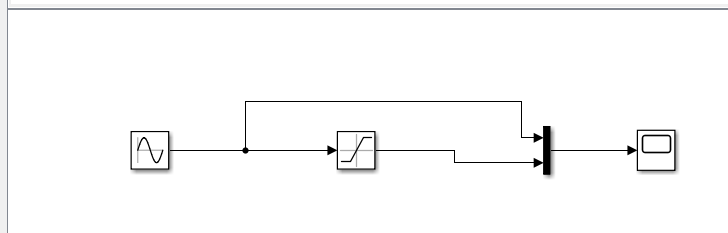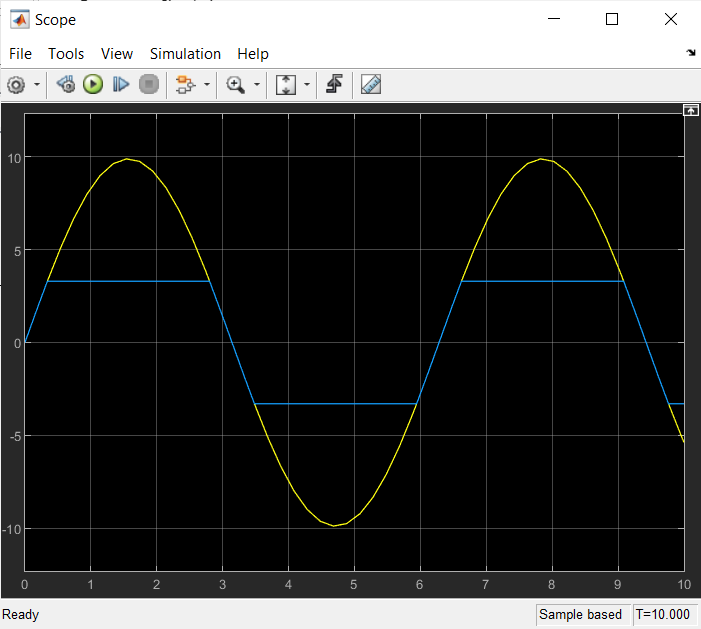
   

2. 
   Сезімталдығы жоқ буын(Dead Zone)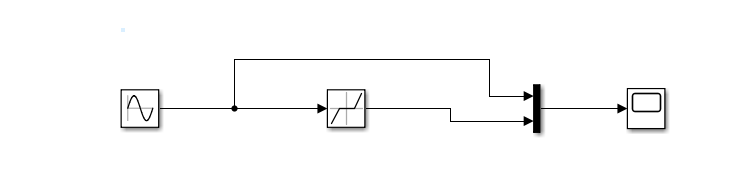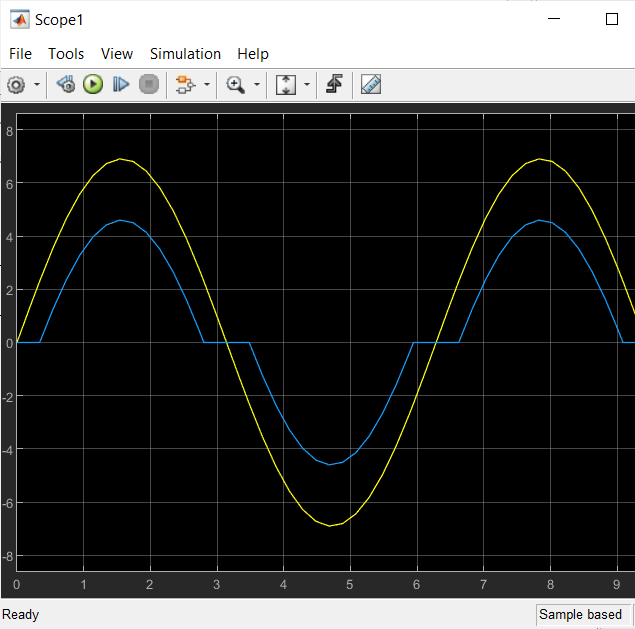
   

3. 
   Гестирезисті бейсызықты буын(Relay)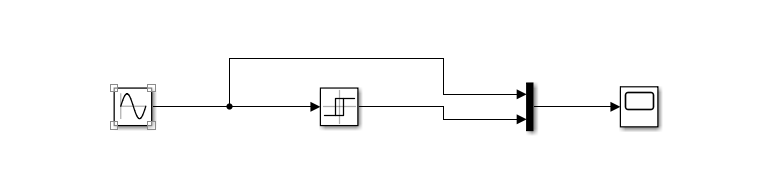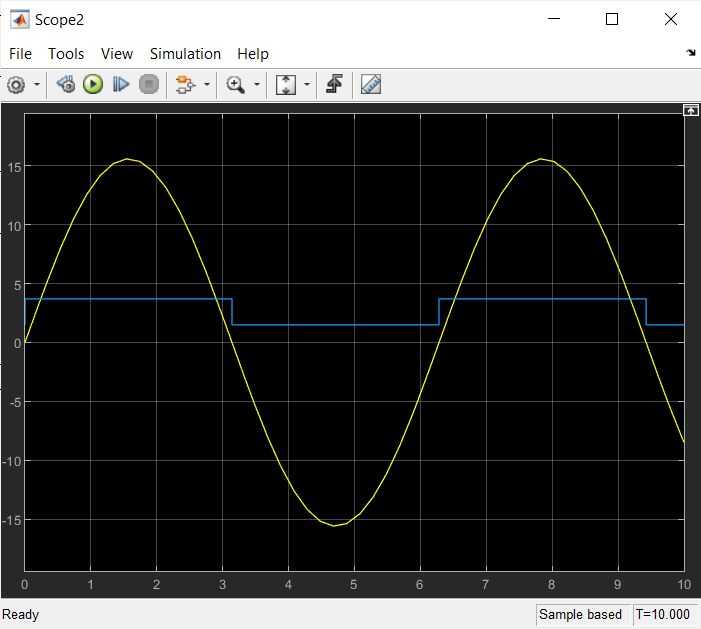
   

4)Квантты буын(Quantizer)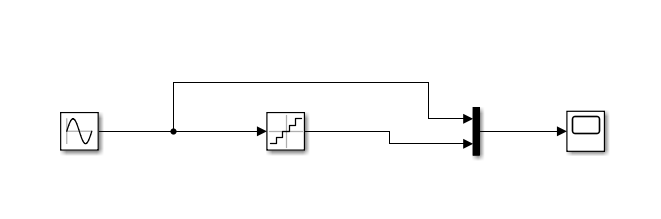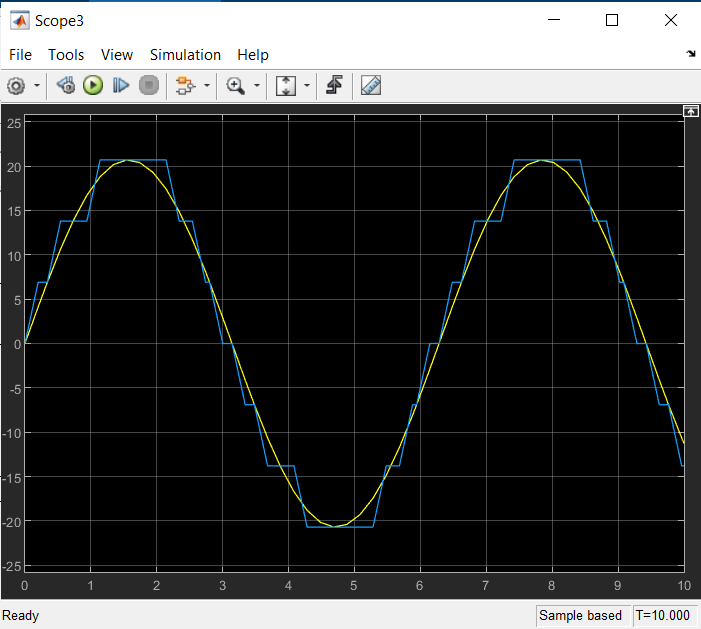



Қорытынды: Мен 4-ші зертханалық жұмыста қарапайым сызықты емес буындармен таныстым және олардың сипаттамаларын зерттедім.

6.4 Бақылау сұрақтары
6.4.1Сызықты емес буындардың түрлері?

а – гистерезис тәрізді; б, в - күшейткішті.

Сызықты емес буындардың түрлері:

•

бір белгілі сипаттамаларынан тұратын сызықты емес буын (статикалық

бейсызықтылық);

•

көп белгілі сипаттамаларынан тұратын сызықты емес буын

(динамикалық бейсызықтылық);

6.4.2Типтік сызықты емес буындар. Типтік динамикалық буындардың

(ТДБ) келесідей түрлері бар: күшейткіш, бірінші ретті апериодты,

тербелмелі, дифференциалдаушы, кешігуші буындар.

6.4.3 Simulink кітапханасының қандай бөлімі сызықты емес жүйелерді

зерттеуге арналған? Simulink бағдарлама кітапханасының Nonlinear

бөлігі сызықты емес бөлікке арналған.

6.4.4 Статикалық сипаттама деген не? Буынның статикалық

сипаттамасы деп тұрақты әсер ету кезінде орнықты режімде шығыс

шаманың кірістің шамасынан тәуелділігін айтады, яғни y(t) = f (x) =

y(x) тепе-теңдік жағдайы.

6.4.5 Сызықты емес жүйе анықтамасы. Сызықты емес АБЖ – ең

болмағанда бір буында сипаттама сызықтылығы немесе теңдеу

сызықтылығы бұзылатын жүйе.

6.4.6 Кіріс шығыс шамалары.

y - шығыс шама;

x, f - кіріс шамалар

6.4.7 Жүйенің эквивалентті беріліс функцияның түрі қандай

Буындардың тізбектей қосылуы. Буындардың тізбектей қосылған тізбегін

эквивалентті түрлендіру арқылы бір буынға ауыстыруға болады. Буынның

беріліс функциясы W(s) жеке буындардың беріліс функцияларын

көбейтуге тең.
бұл кезде комплексті коэффициенттерінің модулі көбейтіледі, ал

аргументтер жинақталады.