Проекциялау тәсілдері. Орталы(центрлік) жне параллель
 Скачать 59.68 Kb.
|
|
Проекциялау тәсілдері Проекциялау әдістері өзінің кескінделу жолдарына байланысты екі түрге бөлінеді: орталық(центрлік) және параллель проекция әдістері. Төменде осы проекциялау әдістерінің пайда болу жолдарын қарастырамыз. Орталық проекция әдісі.Кеңістікте орналасқан кескіндеу жазықтығы П0 мен кескіндеу орталығы S нүктесін және кеңістікте орналасқан геометриялық фигураларды алып, орталықтан проекциялау әдісін салуға болады (39- сурет). Мысал ретінде кеңіс-тікте орналасқан АВ кесін-дісі мен кескінделуші П0 жазықтығын және кескіндеу S нүктесін алайық. Осы S кескіндеу нүктесінен кеңіс-тікте орналасқан АВ кесін-дісінің А және В төбелері арқылы өтетін кескінделуші сәулелер жібереміз. 39-суретте көрсетілгендей бұл сәулелер (s) кескінделуші П0 жазықтығын А0 және В0 нүктелерінде қиып өтеді. Осы А0 және В0 нүктелерін өзара қоссақ, біз кеңістіктегі АВ кесіндісінің кескінделуші П0 жазықтығындағы бір нүктеден (орталықтан) шыққан проекциясын табамыз. Сонымен, егер кескінделуші сәулелер бір нүктеден шыққан немесе тараған болса, онда мұндай проекция тәсілін бір нүктеден немесе орталықтан (центрлік) проекциялау әдісі дейді. Параллель проекциялау әдісін салу үшін келесі мысалды қарастырайық. Кеңістікте орналасқан АВ кесіндісі мен кескінделуші П0 жазықтығы берілсін. Осы кеңістікте орналасқан АВ кесіндісінің А және В төбелері арқылы өзара параллель өтетін кескінделуші сәулелер жүргізейік. Бұл сәулелер кескінделуші П0 жазықтығын екі (А0 және В0) нүктеде қиып өтеді. Осы А0 және В0 нүктелерін өзара қоссақ, онда біз кеңістікте орналасқан АВ кесіндісінің кескінделуші П0 жазықтығындағы проекциясын табамыз. Егер кескінделуші сәулелер (s) өзара параллель болса, онда мұндай проекция әдісін параллель проекциялау әдісі дейді (40-сурет). Параллель проекциялау әдісі кескінделуші П0 жазықтығына сәулелердің кескінделулеріне бай-ланысты екі түрге бөлінеді. Егер П0 жазықтығына сәулелер сүйір немесе доғал бұрышпен кескінделсе, онда параллель проекциялау әдісін қиғаш бұрышты параллель проекциялау әдісі дейді (40-сурет). Ал сәулелер П0 жазықтығына тік бұрышпен кескінделсе, онда параллель проекциялау әдісін тікбұрышты параллель проек-циялау әдісі дейді (41-сурет). Тікбұрышты параллель проек-циялау әдісінің дербес түрі сандық белгілері бар проекциялар әдісі (42-сурет). Егер кеңістікте орналасқан нәрсенің (заттың) горизонталь (көлденең) немесе нольдік деңгейлі жазықтығына П0 тікбұрышты проекциялау әдісімен кескінделген кескіні сан арқылы белгіленген болса, онда кескінделу әдісі сандық белгілері бар проекциялар деп аталады. Бұл проекциялау әдісінде горизонталь (көлденең) немесе нольдік деңгейлі жазықтығында П0 орналасқан геометриялық элементтің кескінінің жанына оның осы жазықтық пен кеңістікте орналасқан элементтің ара қашықтығын, яғни оның биіктігін көрсететін санды жазып қояды. Мысал ретінде 42-суретте көрсетілгендей кеңістікте орналасқан АВ кесіндісін аламыз. Кесіндінің А және В төбелерінен көлденең П0 проекция жазықтығына перпенди-куляр сәулелер түсіреміз. Осы сәулелер көлденең П0 проекция жазықтығын қиып өтеді. Табылған нүктелерді латынның бас әрпімен белгілеп, әріптердің астыңғы жағына сан арқылы осы қиылысқан нүктелер мен түзу төбелерінің ара қашықтығын жазып қояды. Егер табылған қиылысу нүктелерін өзара қоссақ, онда кеңістікте орналасқан АВ түзу сызығының көлденең П0 проекция жазықтығындағы сандық белгілері бар проекциясы болады. 3. Нүкте мен түзү сызықтың кешенді сызбасы. Кеңістікте нүкте мен түзу сызық әр түрлі жағдайда кездесуі мүмкін. Кеңістікте орналасқан нүкте түзу сызық бойында орналасуы немесе түзу сызықтан тыс орналасуы мүмкін. Енді осы тақырыпқа мысал ретінде 87-суреттегі нүктелер мен түзудің өзара орналасуларын қарастырайық. Суретте С және D нүктелері мен АВ түзу сызығының горизонталь және фронталь проекция жазықтығындағы эпюрасы берілген. Кеңістікте орналасқан D нүктесі АВ түзу сызығының горизонталь және фронталь проекция жазықтықтарындағы кескіндерінің бойында жатқан нүкте, яғни D нүктесі АВ түзу сызығына тиісті немесе түзу бойында орналасқан нүкте. Ал енді С нүктесін қарастыратын болсақ, онда С нүктесінің фронталь проекциясы С2 нүктесі АВ түзу сызығының фронталь проекция жазық-тығындағы кескін бойында емес тысқары орналасып жатыр. С нүктесінің горизонталь проекциясы С1 нүктесі АВ түзу сызығының горизонталь проекция жазықтығындағы кескін бойында жатыр, яғни кеңістікте орналасқан С нүктесі АВ түзу сызығының сыртында тыс орналасқан түзу бойында жатпайтын нүкте. Егер нүкте кескіні түзу проекциясының бойында жатса, онда нүкте түзуге тиісті немесе бойында жатады. 4. Дербес және жалпы жағдайдағы түзүлер. Жалпы жағдайдағы орналасқан тузулер. 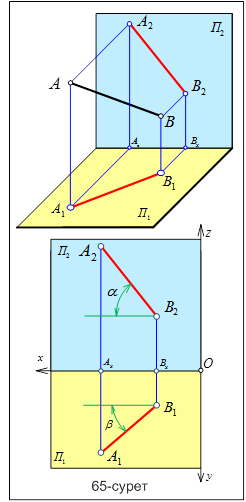 Егер кеңістікте орналасқан түзу сызық горизонталь, фронталь және профиль проекция жазықтықтарына параллель немесе пердендикуляр болмаса және осы жазық-тықтардың бойында жатпаса, онда мұндай түзуді жалпы жағдайда орналасқан түзу сызық дейді (65-сурет). Жалпы жағдайда орналасқан түзу сызық кескіні проекция жазықтықтарына өз шын ұзындығымен (нақты шамасымен) кескінделмейтінін анықтаймыз.65-суреттің жоғарғы жағында түзу сызықтың кеңістіктегі жалпы жағдайда орналасқан АВ түзу сызығы қара түсті сызықпен берілген. Осы кеңістіктегі түзу сызықтың А және В төбелерінен бірінші П1 горизонталь проекция жазықтығына екінші П2 фронталь проекция жазықтығына перпенди-куляр сәулелер жүргіземіз. Бұл сәулелер проекция жазықтықтарымен қиылысып, А1В1 және А2В2 нүктелерін береді. Егер осы табылған нүктелерді өзара қоссақ, онда кеңістікте орналасқан жалпы жағдайдағы түзу сызықтың горизонталь және фронталь проекция жазықтығындағы проекциясын табамыз. Бұл табылған проекциялар қызыл түсті түзу сызықпен көрсетілген. Осы мысалдан жалпы жағдайда орналасқан АВ түзу сызығының көлденең П1 горизонталь проекция жазықтығы мен П2 фронталь проекция жазықтығына жасайтын бұрыштық шамасын α және  бұрыштарын көрсетеміз (65-сурет).Дербес жағдайда орналасқан тузулер. Кеңістіктегі түзу сызықтар өздерінің проекция жазықтықтарына орналасуларына байланысты екі түрге бөлінеді: параллель және проекциялаушы түзулер. Егер кеңістікте орналасқан түзу сызықтың кескіні П1 горизонталь проекция жазықтығына, П2 фронталь проекция жазықтығына және П3 профиль проекция жазықтығына параллель немесе перпендикуляр орналасса, онда мұндай түзулерді дербес жағдайда орналасқан түзулер дейміз. 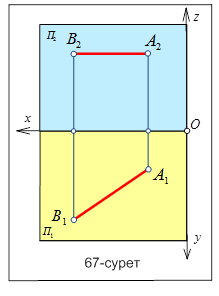 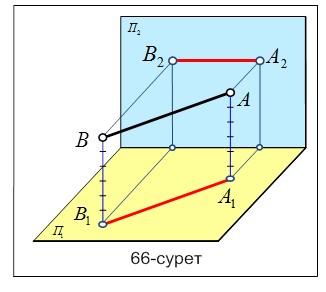 Егер кеңістікте орналасқан түзу П1 горизонталь проекция жазық-тығындағы кескініне немесе түзу сызықтың П2 фронталь проекция жазықтығындағы кескіні х осіне параллель орналасса, онда мұндай дербес жағдайда орналасқан түзулерді параллель түзулер дейді (66-сурет). Мысал қарастыратын болсақ, онда 66-суретте параллель орналасқан түзу сызықтың кеңістікте орналасқан кескіні көрсетілген.Ал 67-суретте кеңістікте орналасқан дербес жағдайдағы параллель түзу сызықтың П1 горизонталь проекция жазықтығымен П2 фронталь проекция жазықтығындағы проекциясы көрсетілген. 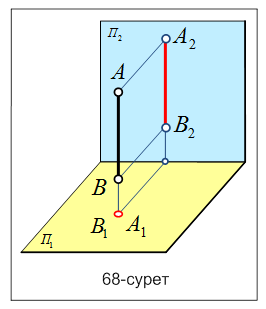 Дербес жағдайда орналасқан параллель түзу сызық проекциясы П1 жазықтығына параллель орналасқандықтан, түзудің жазықтықтағы кескіні нақты шамасымен кескінделеді, яғни түзу сызықтың П1 проекция жазықтығындағы кескіні түзудің шын ұзындығы (нақты шамасы) болады.Енді дербес жағдайда орналасқан проекциялаушы түзуді қарастырайық (68-сурет). Егер дербес жағдайда орналасқан түзу сызық П1 проекция жазықтығына перпендикуляр (тікше) орналасса, яғни түзудің П1 горизонтальпроекция жазықтығындағы проекциялары бір нүктеде беттескен бір ғана нүкте болса, онда мұндай түзу сызықты горизонталь проекциялаушы түзу сызық дейді. 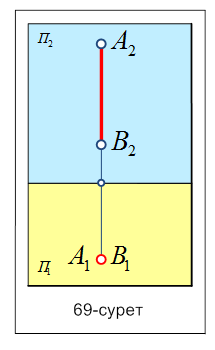 68-суретте горизонталь проекциялаушы түзу сызықтың кеңістікте орналасқан кескіні көрсетілген. Суретте түзу сызықтың кеңістіктегі орналасуын қара сызықпен көрсетсек, фронталь проекция жазықтығындағы кескінін қызыл түсті сызықпен көрсетілген.Ал 69-суретте кеңістікте орналасқан түзу сызықтың эпюрасы, яғни түзудің көлбеу П1 проекция жазықтығындағы кескіні мен П2 проекция жазықтығындағы проекциясы көрсетілген. Дербес жағдайда орналасқан горизонталь проекциялаушы түзу сызық П1 проекция жазықтығына перпендикуляр орналасқандықтан, түзу сызықтың П2 проекция жазықтықтағы кескіні шын ұзындығымен кескінделеді. Түзу сызықтың П2 проекция жазықтығындағы кескіні түзудің нақты шамасы болады, ол сызық қызыл түспен сызылған, өйткені түзу сызық П2 фронталь проекция жазықтығына параллель орналасқан. |