Ортогональное проектирование. Перпендикуляр и наклонная. Угол между прямой и плоскостью
 Скачать 294.71 Kb. Скачать 294.71 Kb.
|
|
Сабақтың тақырыбы: Ортогональ проекциялау. Перпендикуляр және көлбеу. Түзу мен жазықтық арасындағы бұрыш. Тема урока: Ортогональное проектирование. Перпендикуляр и наклонная. Угол между прямой и плоскостью. Сабақтың түрі: құрастырылған Сабақтың мақсаты: Білімділік: студенттерді ортогональ проекциялау ұғымын түсіндіру, ортогональ проекциялар қасиеттерін қарастыру, жазықтыққа түсірілген перпендикуляр, жазықтыққа түсірілген көлбеу, нүктеден жазықтыққа дейінгі қашықтық түсініктерін меңгерту, есептер шығаруда қолдану; есептеу бойынша студентердың білік , дағдыларын қалыптастыру. Дамытушылық: ойлау жүйелілігін және талдау, салыстыра білу қабілетін дамыту; іздену, бақылау арқылы студенттердің дүние таным қабілеттерін қалыптастыру. Тәрбиелік: өз бетінше жұмыс істеуге бейімделу; пәнге деген қызығушылықтарын арттыру; тиянақтылыққа, жылдам ойлауға үйренеді. Сабақтың барысы. I. Ұйымдастыру кезеңі. Сәлемдесу. Студенттерді тугелдеу. Сабақтың тақырпты, мақсатын, жүру барысын айту. ІІ. Өткен сабакты қайталау. Геометриялық диктант. Мәлімдеме рас па? (1 - иә; 0 - жоқ). 1. Осы жазықтықта жатқан екі түзуге перпендикуляр болса, түзу жазықтыққа перпендикуляр бола ма? 2. Егер осы жазықтықта жатқан бір түзуге перпендикуляр болса, түзу жазықтыққа перпендикуляр бола ма? 3. Үш сызыққа перпендикуляр екі сызық параллель тұр ма? 4. Түзу жазықтыққа перпендикуляр болады, егер ол осы жазықтықта жатқандарға перпендикуляр болса: А) үшбұрыштың екі жағы? B) шаршының екі жағы? C) параллелограммның диагоналдары? Геометрический диктант. Верно ли утверждение? (1 – да; 0 – нет). Прямая перпендикулярна плоскости, если она перпендикулярна двум прямым, лежащим в этой плоскости? Прямая перпендикулярна плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости? Две прямые, перпендикулярные третьей прямой, параллельны? Прямая перпендикулярна плоскости, если она перпендикулярна лежащим в этой плоскости: А) двум сторонам треугольника? Б) двум сторонам квадрата? В) диагоналям параллелограмма? ІІІ. Жаңа сабақты түсіндіру. https://bilimland.kz/kk/courses/math-kz/geometriya/stereometriya/kengistiktegi-perpendikulyarlyq/lesson/perpendikulyar-zhane-kolbeu Кеңістіктік фигураларды жазықтыққа кескіндеу үшін параллель проекциялауды пайдаланады. Фигураны кескіндеудің осы тәсілі: Кеңістікте F фигурасы мен α жазықтығы берілсін, α жазықтығын қиятын l түзуін аламыз. F фигурасының әрбір нүктесінен l түзуіне параллель түзулер жүргізіміз.Бұл түзулер α жазықтығымен қиылысқанда, F жазық фигурасы шығады. Ж  азық F фигурасы l түзуіне параллель проекциялаудан алынған F фигурасының α жазықтығындағы проекциясы деп аталады.Мұндағы l түзуі – проекциялаушы түзу, α – проекция жазықтығы. азық F фигурасы l түзуіне параллель проекциялаудан алынған F фигурасының α жазықтығындағы проекциясы деп аталады.Мұндағы l түзуі – проекциялаушы түзу, α – проекция жазықтығы.      Анықтама.Проекциялау жазықтығына перпендикуляр түзу бағытында параллель проекциялауды ортогональ проекциялау деп атайды. Ортогональ проекциялау параллель проекциялаудың бір түрі болғандықтан, ол параллель проекциялаудың барлық қасиеттеріне ие болады.Тікбұрышты проекциялау (ортогональ проекциялау) – параллель проекциялау түрлерінің бірі. 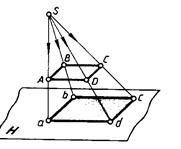 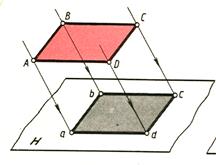 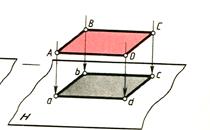 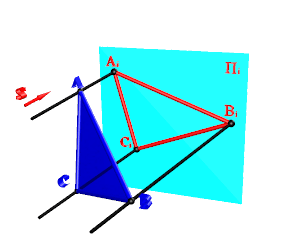 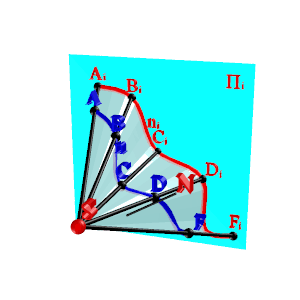 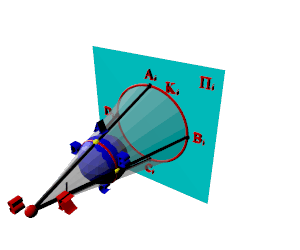 Анықтама.Берілген нүктеден берілген жазықтыққа түсірілген перпендикуляр деп берілген нүкте мен жазықтықты қосатын және осы жазықтыққа перпендикуляр түзудің бойында жататын кесіндіні айтады. Анықтама.Бір ұшы жазықтықта жататын және жазықтыққа перпендикуляр болмайтын кесіндіні жазықтыққа көлбеу деп айтады. [ВС] -- көлбеу, С нүктесі көлбеудің табаны. Перпендикуляр мен көлбеудің табандарын қосатын кесіндіні көлбеудің проекциясы деп атайды. [АС] - көлбеудің проекциясы. [АВ] - перпендикуляр, А - нүктесі перпендикулярдың табаны 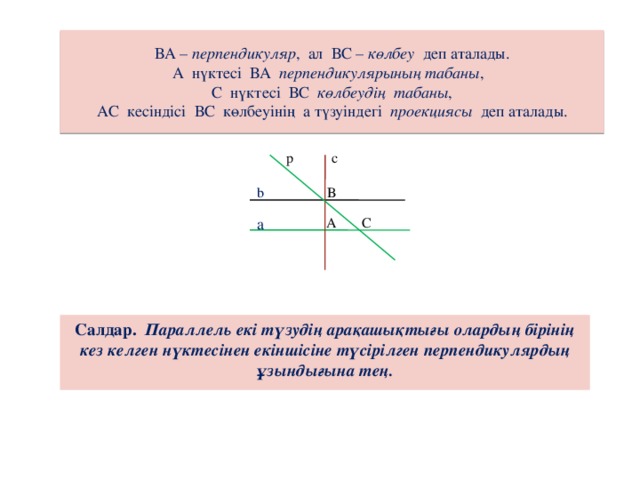 Анықтама.Нүктеден жазықтыққа дейінгі қашықтық деп нүктеден жазықтыққа түсірілген перпендикулярдың ұзындығын айтады. Анықтама: Түзу мен жазықтықтың арасындағы бұрыш деп көлбеу мен оның жазықтықтағы проекциясы арасындағы бұрыш аталады. https://bilimland.kz/kk/courses/math-kz/geometriya/stereometriya/kengistiktegi-perpendikulyarlyq/lesson/tuzu-men-jazyktyktyn-arasyndagy-burysh - Жазықтық пен жазықтықта жатқан түзу немесе жазықтыққа параллель түзу арасындағы бұрыш 00 -қа тең деп есептеледі. - Жазықтық пен перпендикуляр түзу арасындағы бұрыш 900 -қа тең. - Кесінді мен жазықтықтың арасындағы бұрыш депосы кесіндіні қамтитын түзу мен жазықтық арасындағы бұрышты айтамыз. - Параллель түзулердің берілген жазықтықпен жасайтын бұрыштары тең. ІІІ. Объяснение нового материала. https://bilimland.kz/ru/courses/math-ru/geometriya/stereometriya/perpendikulyarnost-v-prostranstve/lesson/perpendikulyar-i-naklonnaya Определение: Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. 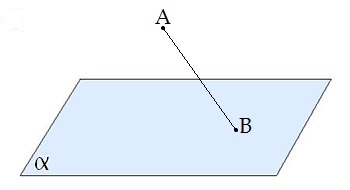 AB - наклонная. B - основание наклонной. AB - наклонная. B - основание наклонной.Определение: Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.  AC - перпендикуляр. C - основание перпендикуляра. Расстоянием от точки до плоскости называется длина перпендикуляра, проведенного из этой точки к плоскости. Определение: Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной. 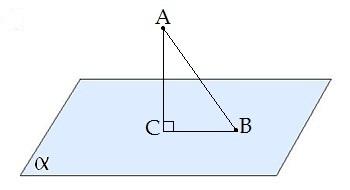 CB - проекция наклонной AB на плоскость α. Треугольник ABC прямоугольный. Определение: Углом между наклонной и плоскостью называется угол между этой наклонной и её проекцией на плоскость. https://bilimland.kz/ru/courses/math-ru/geometriya/stereometriya/perpendikulyarnost-v-prostranstve/lesson/ugol-mezhdu-pryamoi-i-ploskostyu 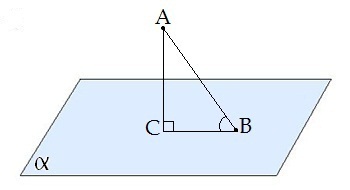 ∢CBA - угол между наклонной AB и плоскостью α. 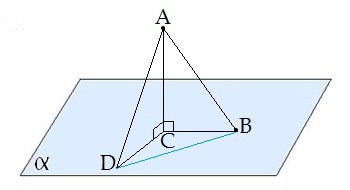 Если AD>AB, то DC>BC Если из данной точки к данной плоскости провести несколько наклонных, то большей наклонной соответствует большая проекция. ∢DAB - угол между наклонными ∢DCB - угол между проекциями Отрезок DB - расстояние между основаниями наклонных. Изучим самый простой, но наиболее важный из способов проектирования в пространстве – ортогональное проектирование. «Ортогональный» в переводе значит «прямоугольный». Ортогональное проектирование является частным случаем параллельного проектирования. Определение. Частный случай параллельного проектирования, при котором направляющая прямая a перпендикулярна плоскости проекций называется ортогональным (орт – перпендикуляр) Ортогональной проекцией фигуры F на плоскости P является фигура, состоящая из ортогональных проекций всех точек фигуры F. 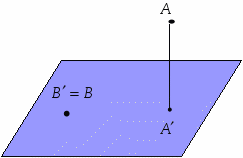 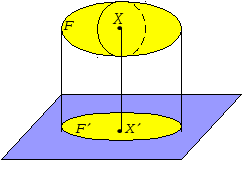 Ортогональное проектирование обладает всеми свойствами параллельного проектирования. Свойство 1. Если прямая перпендикулярна плоскости проектирования, то ее ортогональной проекцией является точка. Если прямая не перпендикулярна плоскости проектирования, то ее ортогональной проекцией является прямая. Свойство 2. Ортогональное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой. В частности, при ортогональном проектировании середина отрезка переходит в середину соответствующего отрезка. Свойство 3. Если две параллельные прямые не перпендикулярны плоскости проектирования, то их ортогональными проекциями являются две параллельные прямые или одна прямая. Заметим, что ортогональное проектирование, также как и параллельное проектирование, не сохраняет длины отрезков и величины углов. Свойство 4. Длина отрезка равна длине его проекции, делённой на косинус угла наклона отрезка к плоскости проекций. Теорема о проецировании прямого угла: Если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна, то угол на эту плоскость проецируется в натуральную величину. ІV.Жана сабақты бекіту. Закрепление пройденного материала. Тақырыпқа байланысты есептер шығару. I тапсырма. Берілгені:  , АС ┴ ВС, SA = SB = SC =10 см; СМ =5 см –медиана. , АС ┴ ВС, SA = SB = SC =10 см; СМ =5 см –медиана.Табу керек: SM (S нүктесінен (АВС) жазықтығына дейінгі қашықтық). 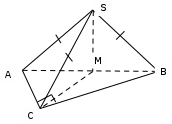 Шешуі: Шешуі:SM түзуі, М –АВ гипотенузаның ортасы, (АВС), SM ┴ (АВС). SM = 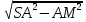 = =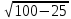 = = 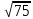 =5 =5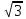 (см). (см).Жауабы: 5 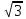 (см). (см).II тапсырма. Берілгені: ABCD – тіктөртбұрыш; АК ┴ (АВС), KD= 6 см, КВ = 7 см, КС = 9 см. Табу керек : К нүктесінен (АВС) жазықтығына дейінгі қашықтық. Ш  ешуі: ешуі:АК – К нүктесінен (АВС) жазықтығына дейінгі қашықтық. DC ┴ AD, AD - KD-ның проекциясы, онда KD┴DC, яғни 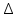 KDC-нан KDC-нан 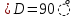 . KC2 = KD2 + DC2, DC = . KC2 = KD2 + DC2, DC = 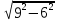 = = 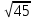 = 3 = 3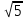 (см). (см).СВ┴КВ; СВ = 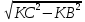 ; СВ = 4 ; СВ = 4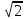 (см). (см).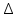 ADC-нан ADC-нан 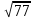 (см). (см).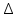 КСА-нан < A = 90º, KA = КСА-нан < A = 90º, KA = 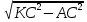 , KA =2 (см). Жауабы: 2 см. , KA =2 (см). Жауабы: 2 см.III тапсырма. Берілгені: АВ = 17 см, АС = 15 см, ВС = 8 см, АМ ┴ (АВС), АМ = 20 см.  Табу керек: МЕ. Табу керек: МЕ.Шешуі: 1. 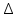 АВС-да кіші қабырғаға қарсы кіші бұрыш жатады. (синустар теоремасы). АЕ ┴ ВС, АЕ ┴ МЕ жүргіземіз. Үш перпендикуляр туралы теорема бойынша МЕ ┴ ВС. АВС-да кіші қабырғаға қарсы кіші бұрыш жатады. (синустар теоремасы). АЕ ┴ ВС, АЕ ┴ МЕ жүргіземіз. Үш перпендикуляр туралы теорема бойынша МЕ ┴ ВС.2. Герон формуласы бойынша: S  = = 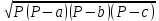 , S , S = =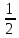 BC·AE. BC·AE.P = 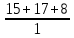 = 20, S = 20, S = =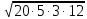 = 60. = 60.AE = 15 (см). Пифагор теоремасы бойынша: МЕ = 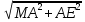 , МЕ = 25 (см). , МЕ = 25 (см).Ж  ауабы: 25 см. ауабы: 25 см.V. Қорытындысы. Рефлексия. VI. Үй тапсырмасы. Домашнее задание. Сұрақтарға жауап беріңіз: «иә» (+), «жоқ» (-), «білмеймін» (0). Ответить на вопросы: «Да» (+), «Нет» (-), «Не знаю» (0). I тапсырма. Осы жазықтықта параллельді проекциялау кезінде: 1. екі тең емес кесінді тең проекцияларға ие бола алады ма; 2. Түзудің проекциясы кесінді бола алады; 3. Параллель сызықтарды құрайтын қиылысатын сызықтар бар; 4. Шеңбердің проекциясы кесінді бола алады; 5. Шеңбердің проекциясы оған тең емес шеңбер болуы мүмкін. При параллельном проектировании на данную плоскость: два неравных отрезка могут иметь равные проекции; проекцией прямой может быть отрезок; Найдутся такие скрещивающиеся прямые, которые проектируются в параллельные прямые; Проекцией окружности может быть отрезок; Проекцией окружности может быть неравная ей окружность. II тапсырма. Ортогональды проекциялау нәтижесінде: 1. Квадраттың проекциясы квадрат болуы мүмкін; 2. Квадраттың проекциясы тең емес жақтары бар тіктөртбұрыш болуы мүмкін; 3. Кубтың проекциясы квадрат бола алады; 4. Доптың проекциясы шеңбер бола алмауы мүмкін. В результате ортогонального проектирования: проекцией квадрата может быть квадрат; проекцией квадрата может быть прямоугольник с неравными сторонами; проекцией куба может быть квадрат; Проекцией шара может быть не круг. VII. Бағалау. Выставление оценок. |
