СЫЗЫҚТЫҚ АВТОМАТТЫ БАСҚАРУ ЖҮЙЕЛЕР. Приложение. осымша 1 Сипаттамалы полином, із

• Название: осымша 1 Сипаттамалы полином, із
• Анкор: СЫЗЫҚТЫҚ АВТОМАТТЫ БАСҚАРУ ЖҮЙЕЛЕР
• Дата: 14.07.2021
• Размер: 172.5 Kb.
• Имя файла: Приложение.doc
• Тип: Документы; #224285

Қосымша 1
Сипаттамалық полином, із

Матрица А сипаттамалық полиномының маңызды қаксиеті солай қорытындылады, ол матрица А үшін жойғыш болады, яғни Кэлли-Гамильтон теоремасы орындалады.

Матрица сипаттамалық полиномы деп аталады, полином түбірлері s_i – матрица А меншікті мәндері болады.

Теорема қ.1 (Кэлли-Гамильтон). Матрица өзінің сипаттамалық теңдеуін қанағаттандырады, егер , онда .

Салдар. Көрініп тұрғандай, Aⁿ, және оған байланысты А^m, m ≥ n болған кезде төменгі дәрежелер A^k, k = 0, 1, …, n – 1 сызықтық комбинациялары ретінде өрнектеледі.

Осы матрица үшін көп жойғыш матрицалар бар; олардың ішінде ең төменгі дәрежесі μ-ге тең болатыны (және үлкен коэффициенті бірге тең болатыны) минималды полином деп аталады. Осыған сәйкес, А кез келген дәрежесі сызықтық комбинация I, A, …, A^μ-1 ретінде көрсетіледі.

Сипаттамалық полиномның басқа қасиеттерінен бөліп көрсетеміз:

1) ;

2) ;

берілген матрицалар ізінің қасиеті

1) ;

2) , мұндағы λ_i– A меншікті мәндері;

3) .

Қосымша 2
Матрицалық жіктеу
1 Диагональдық тұлғаға келтіру

Лемма қ.1. Егер матрица барлық меншікті мәндері λ_i, i =1,…, n әртүрлі болса, онда ол ұқсастық түрлендірумен диагональдық түрге келтіріледі, яғни сондай азғындалмаған матрица табылады, мына теңдікті қанағаттандыратын
.
Мұнда λ_i матрица А меншікті мәндері, Т – матрица, оның тік жолдары x_i болады және матрица А оң меншікті векторлары; , ал жатық жолдары y_i матрица сол меншікті векторлары матрица А болады: .

Лемма қ.2. Егер , онда ол диагональдық тұлғаға ортогональды ұқсас түрлендірумен келтіріледі, яғни сондай табылады орындалатындай және
,
және барлық меншікті мәндер λ_i нақтылы болады.


2 Жордано тұлғасына келтіру

Лемма қ.3. Кез келген матрица үшін сондай азғындалмаған матрица бар болады,

орындалатын. Мұнда J – матрица А жордано тұлғасы: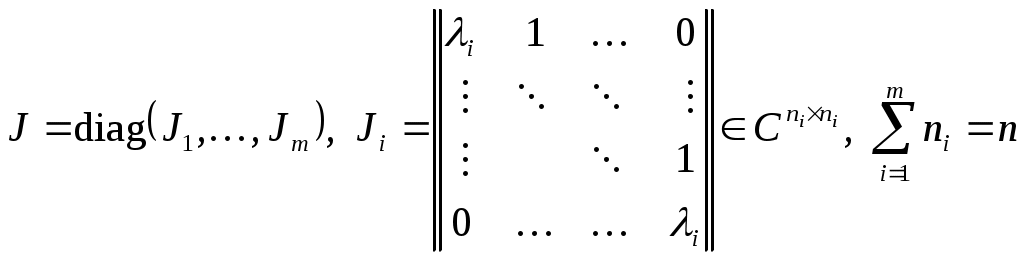
.
Осында λ_i – матрица А меншікті мәндері, ал J_i – жордано блоктары.

3 Фробениус тұлғасына келтіру

Егер матрица 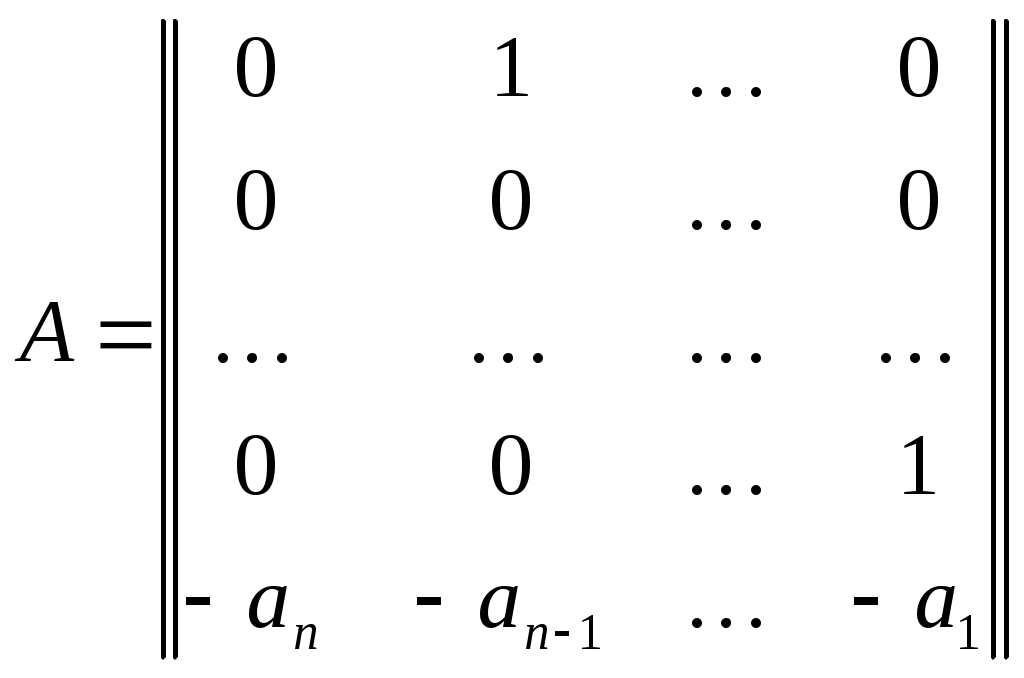үшін сондай вектор табылатын болса, векторлар сызықтық тәуелсіз, онда А циклдық матрица (ал вектор b – оның циклдық генераторы) деп аталады.

Матрица фробениус тұлғасына келтірілген деп айтылады, егер ол келесі түрде болса
, (қ.1)
мұнда . Матрица А сипаттамалық полиномы тең болады
. (қ.2)
Кейде жоғарыдағы матрица (қ.1) полином (қ.2) үшін Фробениус матрицасы деп аталады.

Лемма қ.4. Азғындалмаған ұқсас түрлендіру матрицасы көмегімен матрицаны фробениус тұлғасына келтіруге болады тек сонда, қашан ол циклдық болғанда.

Матрица циклдық болады тек сол жағдайда, қашан оның әр меншікті мәніне дәл бір жордано блогы сәйкес келсе; оған эквиваленттң, қашан оның сипаттамалық полиномы минималды дәл түйіссе.

4 Нақтылы блокты-диагональдық тұлғаға келтіру

Лемма қ.5. Матрица меншікті мәндері әртүрлі болсын. Онда сондай азғындалмаған матрица бар болады, келесі түрлендіру орындалатын
, (қ.3)
мұнда матрицалар төмендегідей түрде болады
.
Осындай жағдайда түрленген матрица Λ нақтылы блокты-диагональдық тұлғалы деп айтылады.

Бұл кез келген матрицаны нақтылы жордано тұлғасына нақтылы матрица Т көмегімен ұқсас түрлендірудің жеке жағдайы болады.

5 Каноникалық басқарылатын тұлға. Басқарылу

Жүйені қарастырайық
(қ.4)
және – матрица А сипаттамалық полиномы болсын.

Лемма қ.6. Егер векторлар 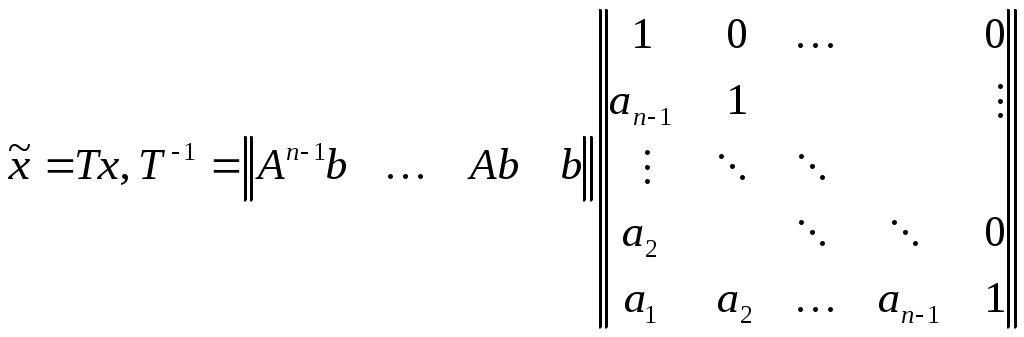сызықтық тәуелсіз болса (яғни жұп (A, b) басқарылады), онда айнымалыларды сызықтық алмастыру арқылы
(қ.5)
жүйе (қ.4) басқарылатын каноникалық тұлғаға келтіріледі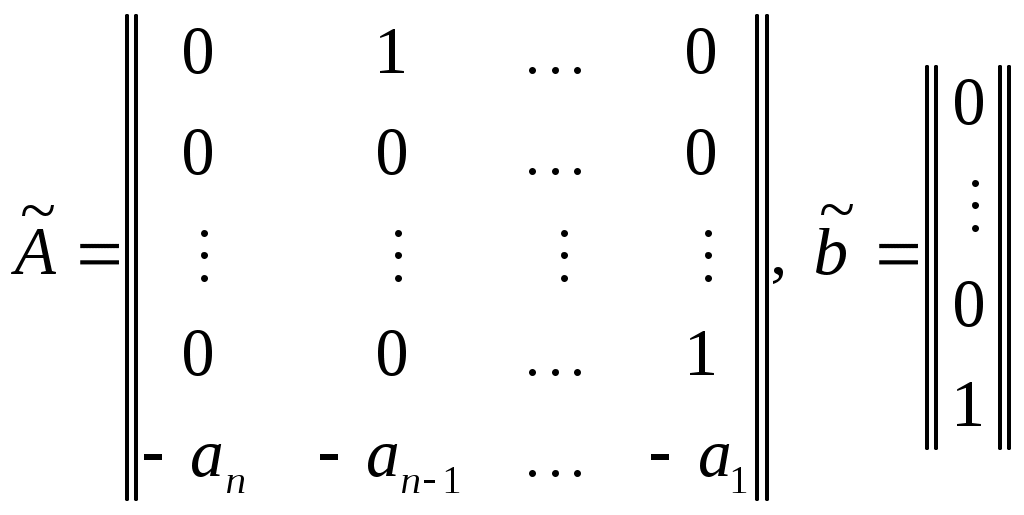
, (қ.6)
. (қ.7)
Осында матрица А ұқсас түрлендірумен фробениус тұлғасына келтірілген.

Теорема қ.2 (Басқарылу). Келесі шарттар эквивалентті:

1. 
   Жүйе
   

басқарылады.

2. 
   Басқарылу граммианы
   

кез келген t > 0 үшін оң-анықталған матрица болады.

3. 
   Басқарылу матрицасы рангысы n болады.
   
4. 
   Хаутус матрицасы кез келген үшін рангысы n болады.
   
5. 
   Матрица таңдау арқылы матрица A + Bk меншікті мәндерін еркін орналастыруға жету мүмкін болады.
   

Қосымша 3
Матрицалық экспонента

Дифференциалдық теңдеулерді талдау кезінде ең көп кездесетін матрицалық функциялар экспоненталар болады. Бүкіл комплекстік жазықтықта f(s) = e^s аналитикалық болғандықтан, қатар түріндегі экспонентаның анықтамасын пайдалану ыңғайлы болады:
.
Осы функцияның бірнеше қасиеттерін келтірейік:

1. ;

2. Егер , онда . Жеке жағдайда, егер A = aI, онда ;

3. Егер матрицалар А және В қатынасатын болса, онда (жалпы айтқанда, керісінше дұрыс болмайды). Басқа жағынан, егер барлық үшін, онда AB = BA;

4. қатынастылық салдарынан, жеке жағдайларда кез келген (азғындалған немесе жоқ) матрица А үшін ;

5. қатынастылық салдарынан;

6. ;

7. Егер матрица А кері аударылатын болса, онда , мұндағы С – қандай да бір тұрақты матрица. Жеке жағдайларда, және орнықты А үшін.