|
|
Осипова Мария Викторовна, учитель математики и информатики 1 категории мбоу сош 9, г. Ковров, Владимирская область
Осипова Мария Викторовна,
учитель математики и информатики
1 категории
МБОУ СОШ №9,
г. Ковров, Владимирская область
Тест по геометрии
«Метод координат»
9 класс
1 вариант
Расстояние между точками А (х1, у1) и В(х2, у2) выражается формулой:
а) 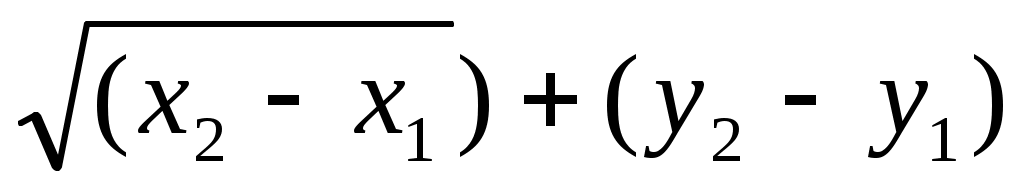  в) в) 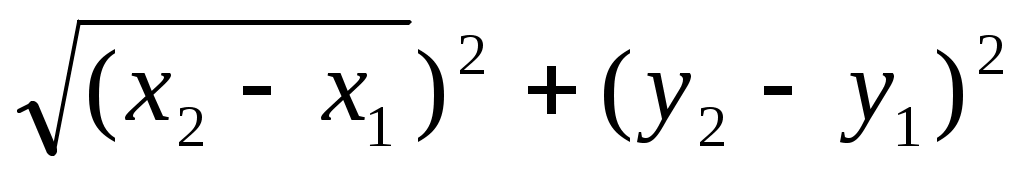
б) 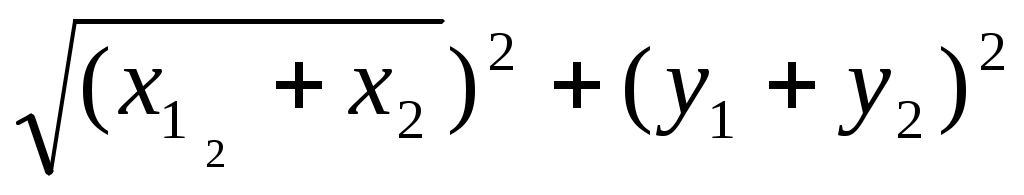 г) (х2 – х1 )2 + (у2 – у1)2 г) (х2 – х1 )2 + (у2 – у1)2
Точка С – середина отрезка АВ , где А(х1, у1) и В(х2, у2). Точка С имеет координаты :
а) С(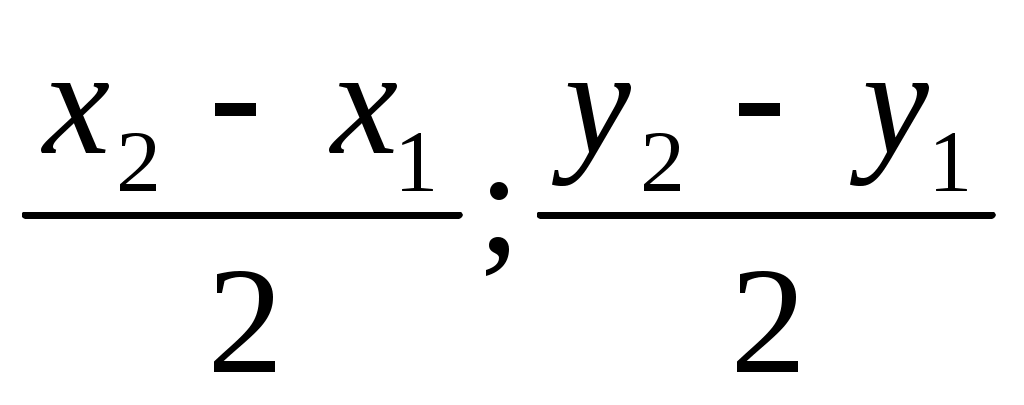 ); в) С( ); в) С(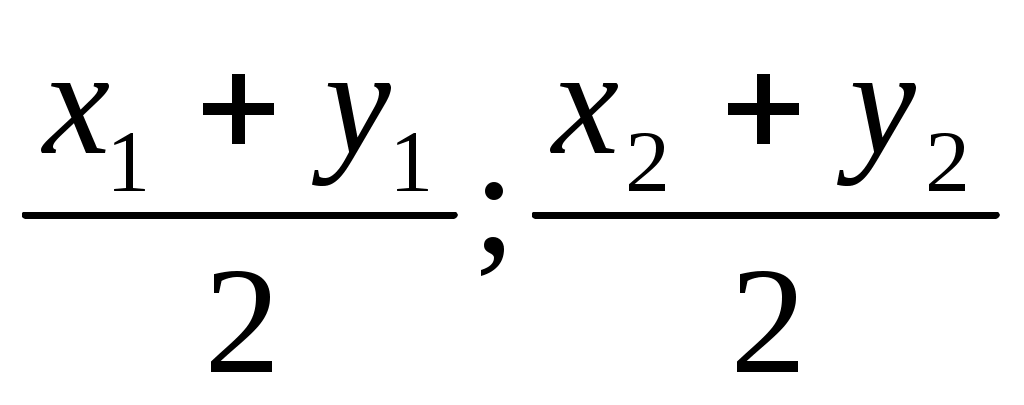 ); );
б) С(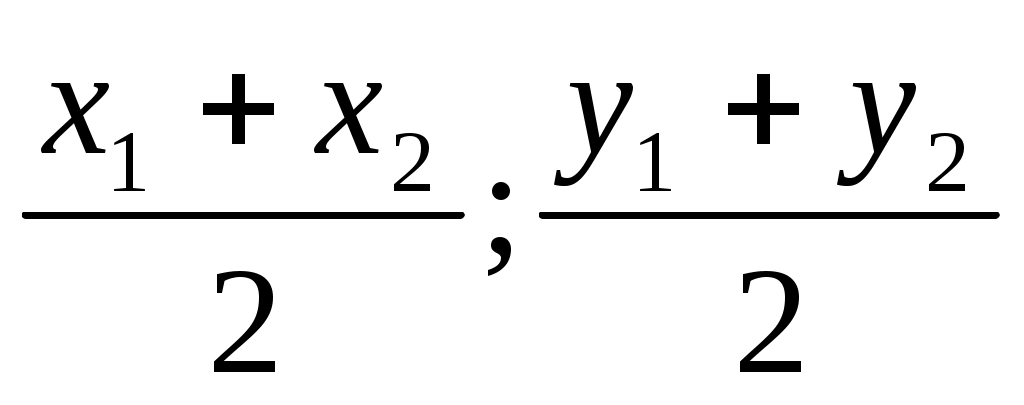 ); г) С(х2 –х1;у2-у1) ); г) С(х2 –х1;у2-у1)
3. Длина вектора а {х;у} выражается формулой:
а) х2 + у2 в) 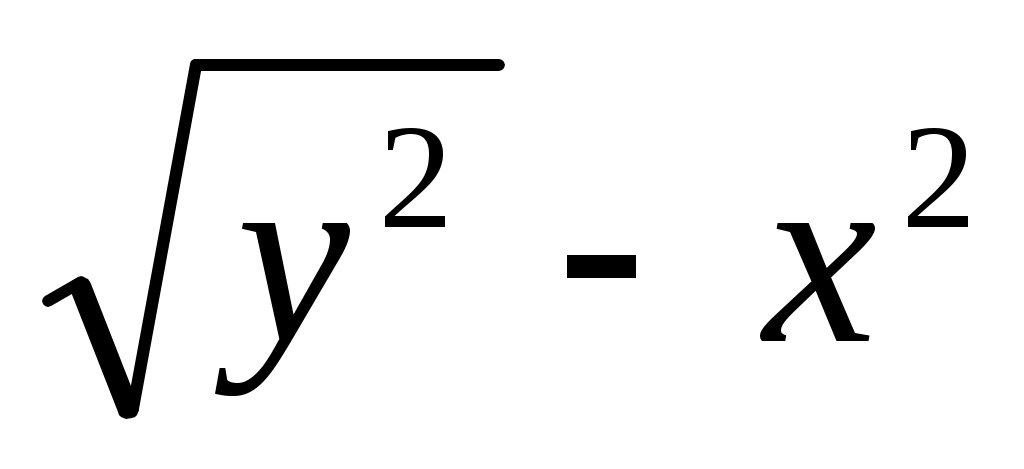
б) 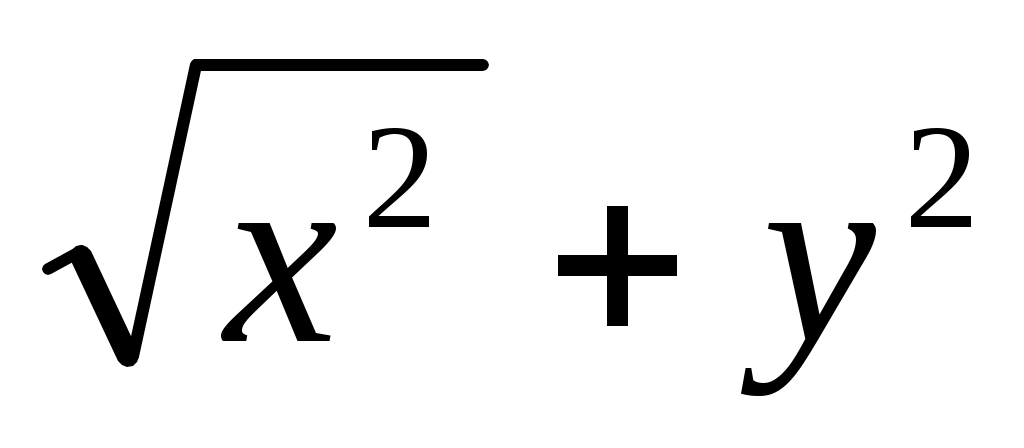 г) г) 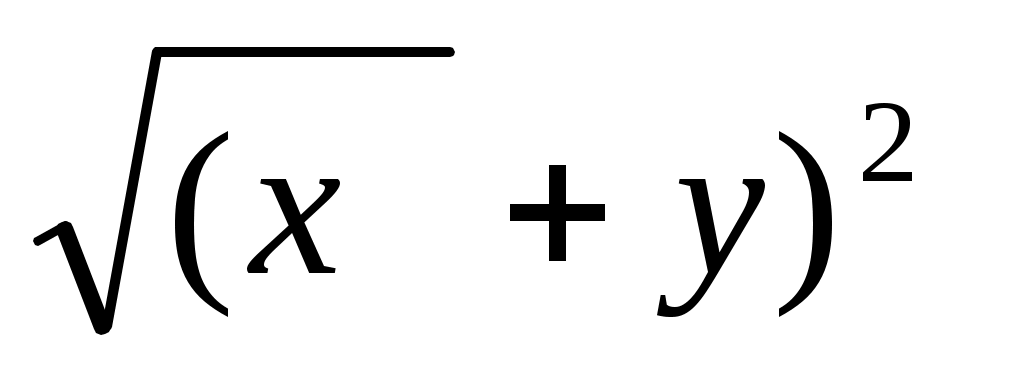
4. Уравнение окружности имеет общий вид, где С(х0; у0) – центр окружности:
а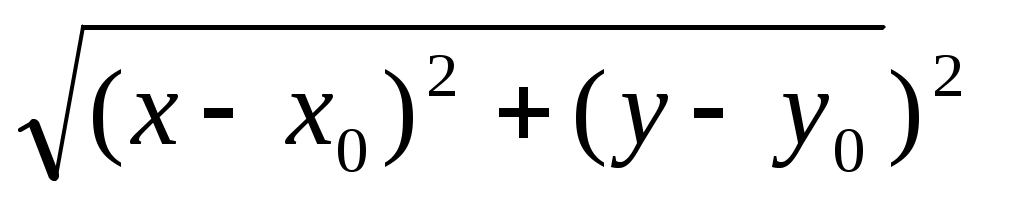 = r2 в) (х – х0 )2 + (у – у0)2 = r2 = r2 в) (х – х0 )2 + (у – у0)2 = r2
б) (х – х0)2 + (у – у0 )2 = r г) (х + х0)2 + (у + у0)2 = r2
Выясните, какие из данных уравнений являются уравнениями окружности:
а) (х-6)2 + (у+5)2 = 12 г) х2+ у2 = -9
б) 4х2+у2 =4 д) х2+(у-1)2 = 16
в) х2 +у2 =0 е) (х+2)2 +у2 = - 25
6. Найти координаты и длину вектора 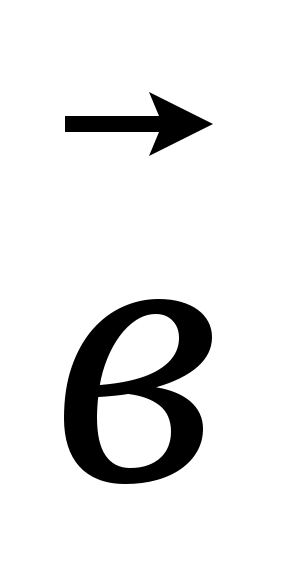 , если , если 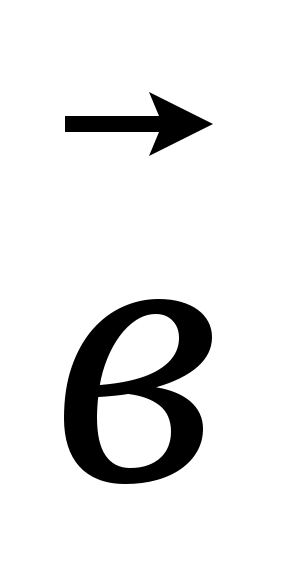 = = 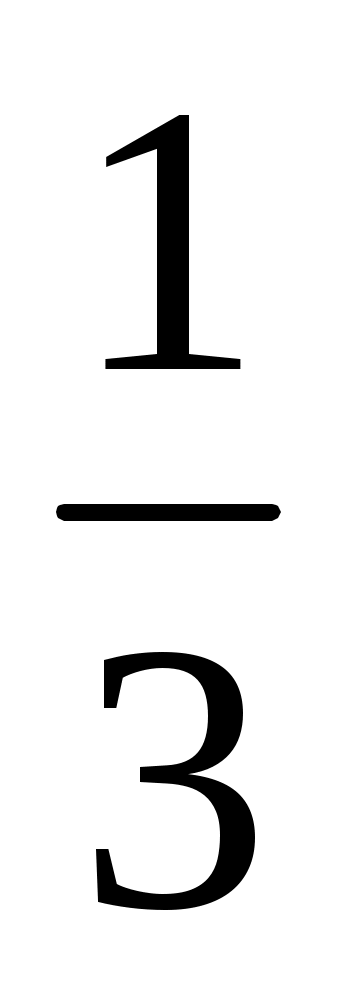 , , 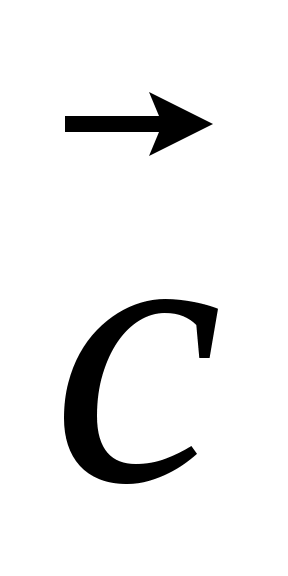 – – 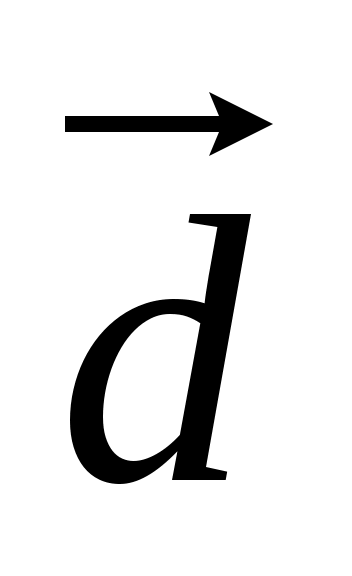 , , 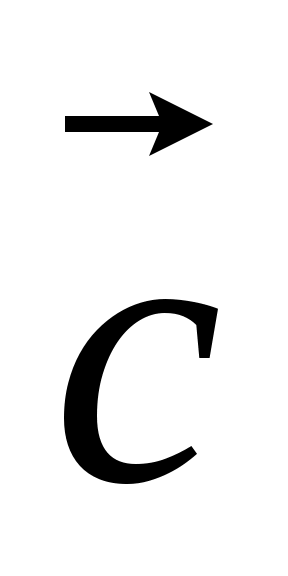 (-3,6), (-3,6), 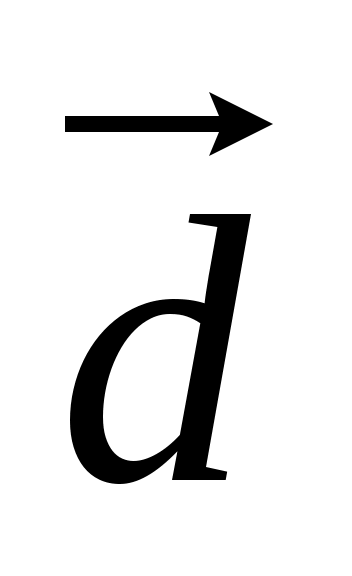 (2.-2). (2.-2).
А(-4,7) и В(16,22).
Найти:
а) координаты вектора 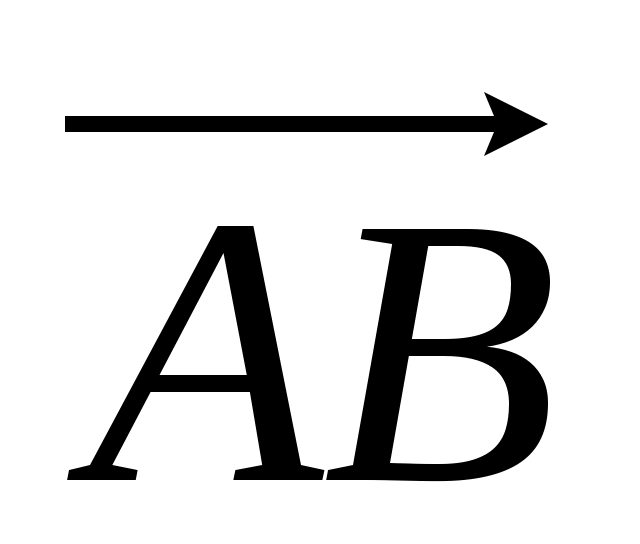
б) длину вектора 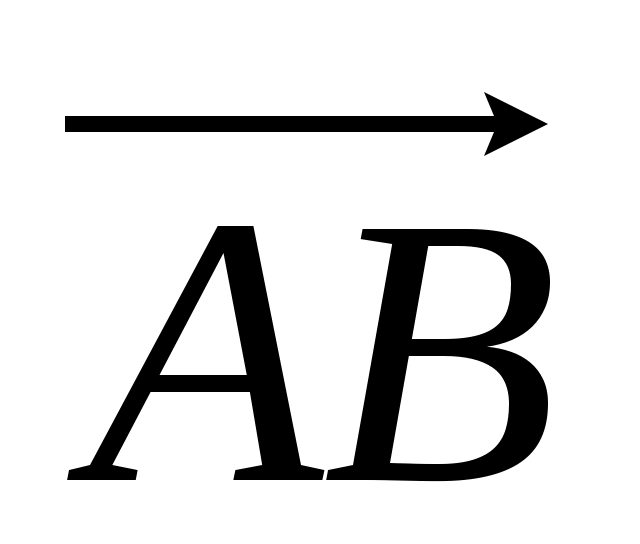
в) координаты середины отрезка АВ
г) записать уравнение окружности с центром в точке А и радиуса АВ
д) уравнение прямой АВ
|
2 вариант
1. Расстояние между точками А(х1, у1) и В(х2, у2) выражается формулой:
а) 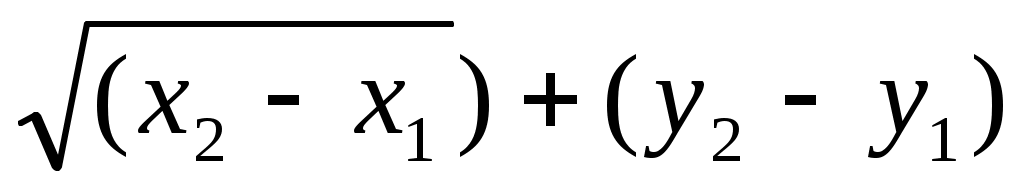  в) в) 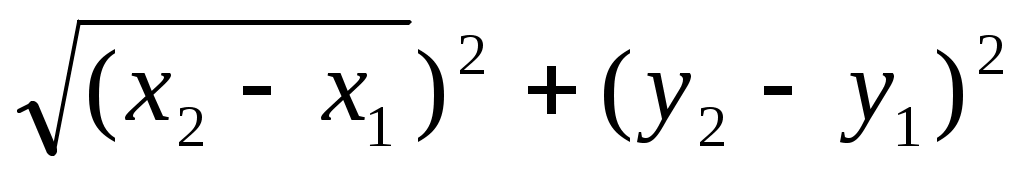
б) 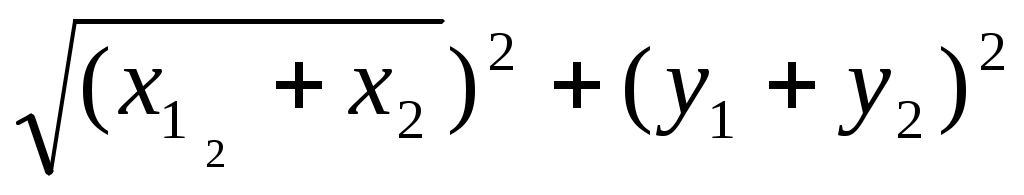 г) (х2 – х1 )2 + (у2 – у1)2 г) (х2 – х1 )2 + (у2 – у1)2
2.Точка С – середина отрезка АВ , где А(х1, у1) и В(х2, у2).
Точка С имеет координаты :
а) С(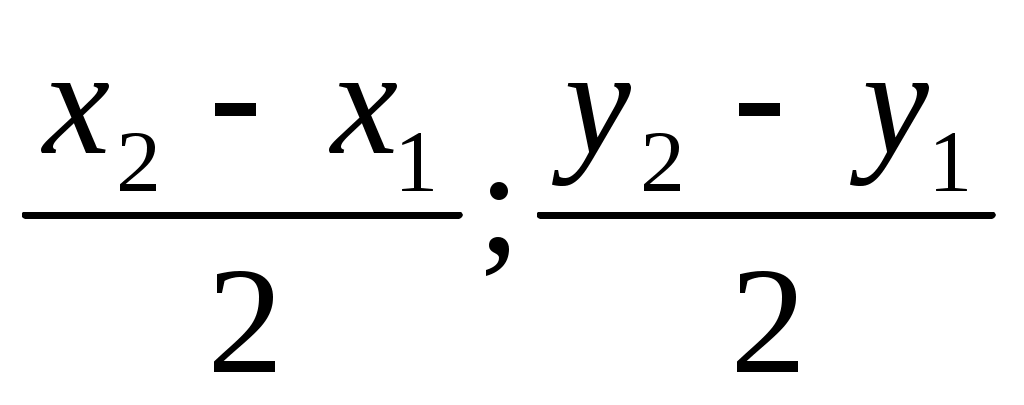 ); в) С( ); в) С(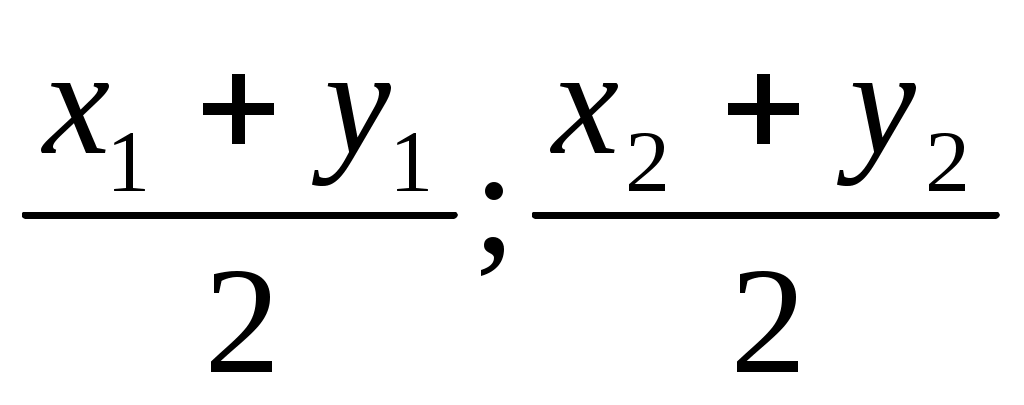 ); );
б) С(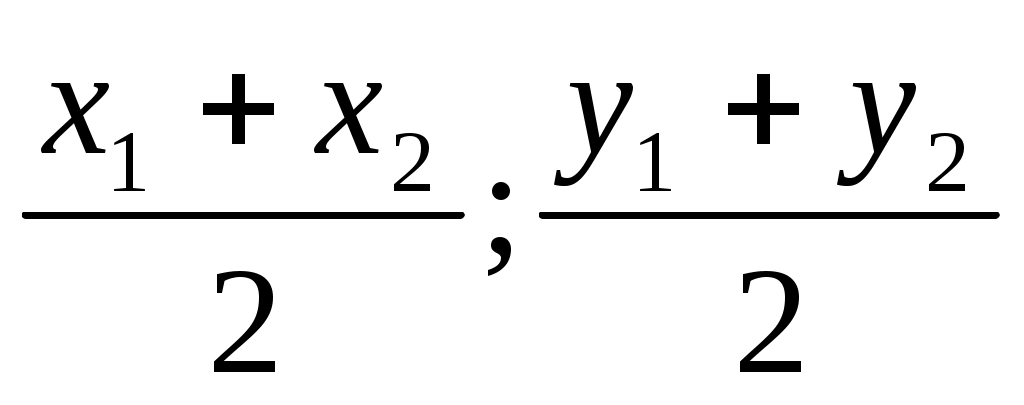 ); г) С(х2 –х1;у2-у1) ); г) С(х2 –х1;у2-у1)
3. Длина вектора а {х;у} выражается формулой:
а) х2 + у2 в) 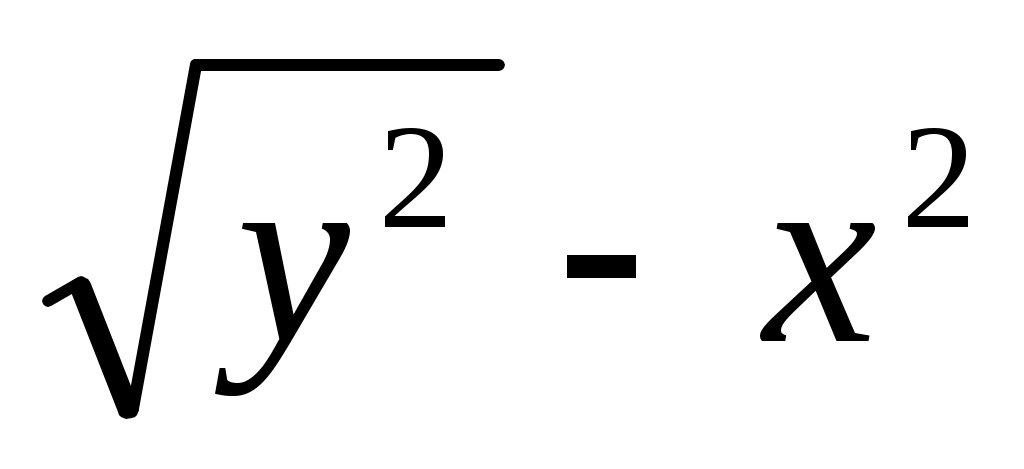
б) 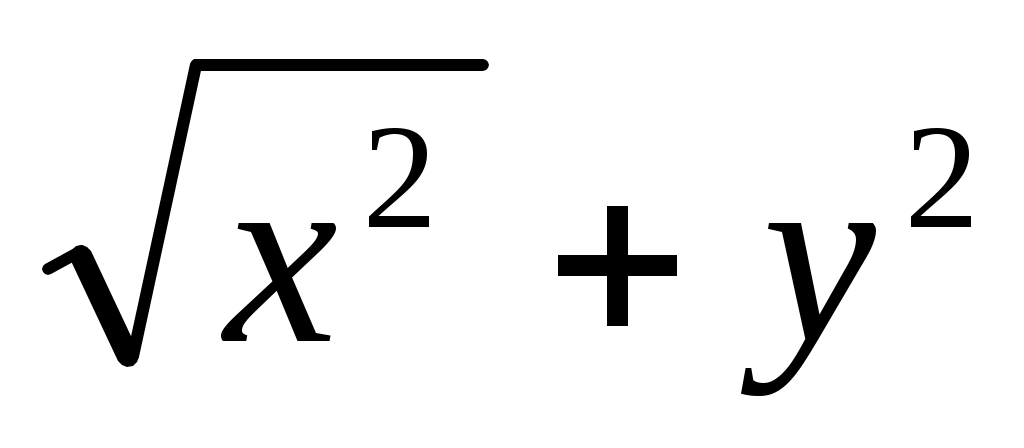 г) г) 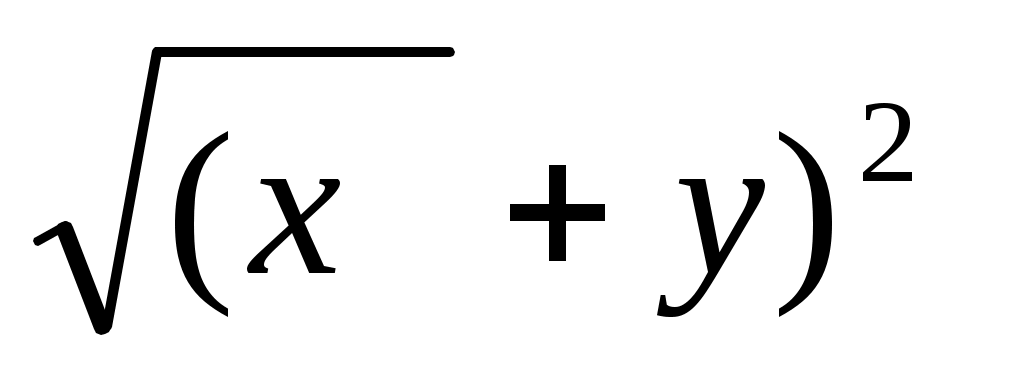
4. Уравнение окружности имеет общий вид, где С(х0; у0) – центр окружности:
а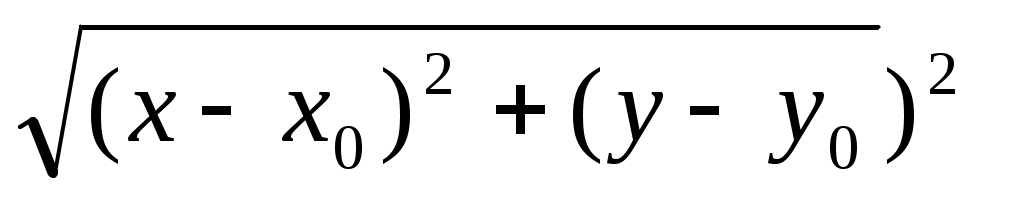 = r2 в) (х – х0 )2 + (у – у0)2 = r2 = r2 в) (х – х0 )2 + (у – у0)2 = r2
б) (х – х0)2 + (у – у0 )2 = r г) (х + х0)2 + (у + у0)2 = r2
5. Выясните, какие из данных уравнений являются уравнениями окружности:
а) (х-6)2 + (у+5)2 = 12 г) х2+ у2 = -9
б) 4х2+у2 =4 д) х2+(у-1)2 = 16
в) х2 +у2 =0 е) (х+2)2 +у2 = - 25
6. Найти координаты и длину вектора 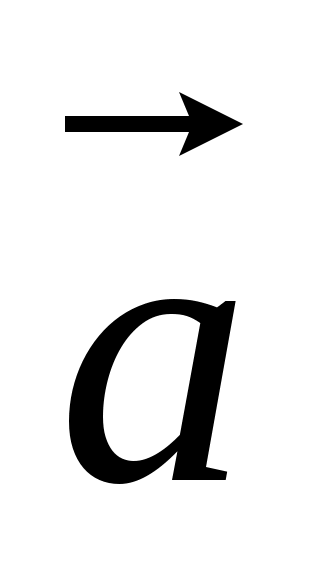 , если , если 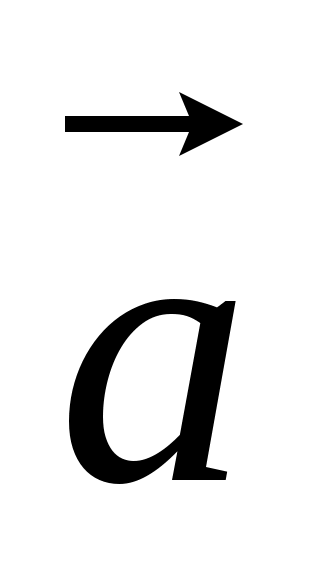 = = 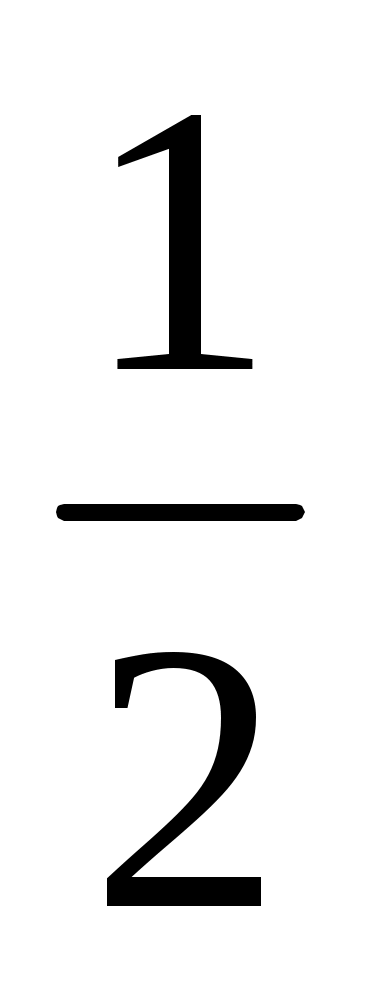 , , 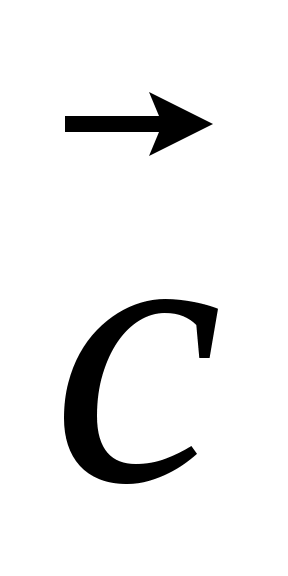 – – 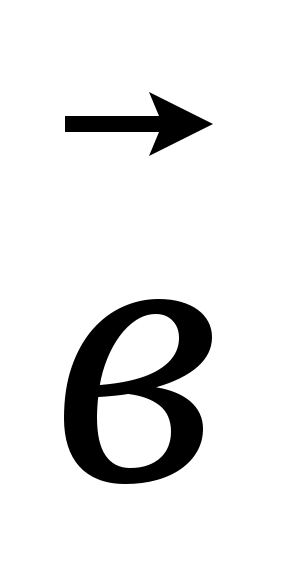 , если , если 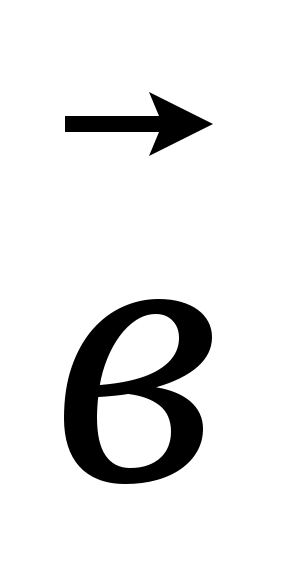 (3,-2), (3,-2), 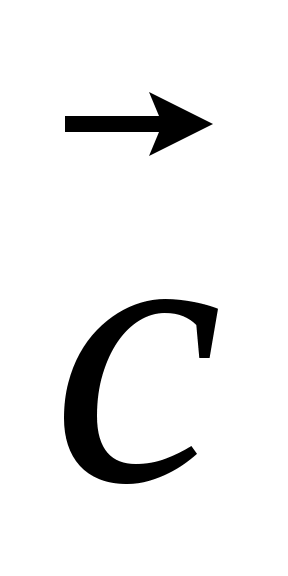 (-6,2) (-6,2)
С(-3,1) и Д(9,6) Найти:
а) координаты вектора 
б) длину вектора 
в) координаты середины отрезка СД
г) записать уравнение окружности с центром в точке С и радиуса СД
д) уравнение прямой СД
| |
|
|
 Скачать 101 Kb.
Скачать 101 Kb.