тидз4. Основы теории кодирования. Код Хемминга Иванов Д. А
 Скачать 64.66 Kb. Скачать 64.66 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра информационных систем ОТЧЕТ по практической работе №4 по дисциплине «Теория информации, данные, знания» Тема: Основы теории кодирования. Код Хемминга Иванов Д.А. Санников Е.С. Коршунова А.С. Студенты гр. 9893  Преподаватель Писарев И. А.  Санкт-Петербург 2021 Цель работы Изучить основы теории кодирования. Сформулировать ответы на вопросы с указанием источников информации. Вопросы по теме 2: Сформулируйте задачу надёжной передачи сообщений. Объясните, почему кодирование с контрольной суммой позволяет обнаружить в процессе передачи только нечётное число ошибок. Дайте определение расстояния Хэмминга между двоичными словами. Какова связь обнаруживающей способности кода с минимальным расстоянием Хэмминга? Решить задачи по теме 2: Для слов длины m = 3 в алфавите B = {0, 1} используются кодовые слова длины n = 4 (3, 4 – коды). Порождающая матрица (3,4) имеет вид: [[1, 0 ,0 ,1], [0, 1 ,0,1], [0, 0,1,1]]. Какую по кратности ошибку может обнаружить этот код? Определите кодовое слово b для слова исходного сообщения a = 001. Какое кодовое слово b соответствует слову исходного сообщения a= 100. Какое кодовое слово b соответствует слову исходного сообщения a= 111. Выполнение работы: Сформулируйте задачу надежной передачи сообщений. Постановка задачи надёжной передачи сообщений состоит в следующем. Пусть по каналу связи требуется передавать слова в некотором алфавите А. На вход канала подаётся слово α, а на выходе принимается искажённое слово w. Требуется по слову w восстановить слово α [2, С.118]. 2 Соответственно формулировка задачи будет выглядеть следующим образом: Задача надежной передачи информации заключается в восстановлении, по искаженным словам, реально отправленных слов. Объясните, почему кодирование с контрольной суммой позволяет обнаружить в процессе передачи только нечётное число ошибок. При кодировании с контрольной суммой используется так называемый разряд четности. Последний символ кода ( 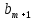 ) равен сумме всех предыдущих по mod 2. Последнее означает, что ) равен сумме всех предыдущих по mod 2. Последнее означает, что 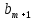 = 0, если сумма предыдущих символов чётная, и = 0, если сумма предыдущих символов чётная, и 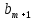 = 1, если сумма предыдущих символов нечётная, так как для любого натурального k значение функции k mod 2 = 0 (для чётных k); либо =1 (для нечётных k). = 1, если сумма предыдущих символов нечётная, так как для любого натурального k значение функции k mod 2 = 0 (для чётных k); либо =1 (для нечётных k).Значение символа 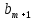 , вычисленное по данному правилу, называется контрольной суммой. , вычисленное по данному правилу, называется контрольной суммой.При нечетном числе ошибок контрольная сумма позволяет обнаружить факт ошибки, а при четном числе ошибок символ кода будет таким же, как и при отсутствии ошибок, потому что она считается как сумма всех предыдущих разрядов по mod 2 [2, C.119]. Дайте определение расстояния Хэмминга между двоичными словами. Определение: пусть x и y – двоичные слова длины m в алфавите B = {0,1}. Расстояние Хемминга между следующим образом: d( x , y ) равно числу несовпадений в соответствующих позициях слов x и y [2, C.121]. Второй пример: пусть x = 110101, y = 011001, z = 000110 → d( x , y ) = 3, d( y , z ) = 5, d( x , z ) = 4. Функция удовлетворяет всем аксиомам расстояния: d( x , y ) ≥ 0, , причём d( x , y ) = 0 только при x = y ; d( x , y ) = d( y , x ); d( x , z ) ≤ d( x , y ) + d( y , z ) – неравенство треугольника. 3 Какова связь обнаруживающей способности кода с минимальным расстоянием Хэмминга? При взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наименьшем числе символов. Степень различия любых двух кодовых комбинаций характеризуется расстоянием между ними (по Хэммингу), или просто кодовым расстоянием. Оно выражается числом символов, в которых комбинации отличаются одна от другой, и обозначается через d. Чтобы рассчитать кодовое расстояние между двумя комбинациями двоичного кода, достаточно подсчитать число единиц в сумме этих комбинаций по модулю 2, например заданы две кодовые комбинации А и В. Требуется определить кодовое расстояние. Складывая по модулю 2 А и В, получаем некоторую комбинацию С. Непосредственный подсчет единиц определяет вес ϖ(С) кодовой комбинации С, который равен кодовому расстоянию d. 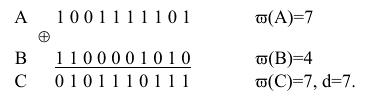 Минимальное расстояние, взятое по всем парам кодовых комбинаций данного кода, называется минимальным кодовым расстоянием. Декодирование после приема может производиться таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая отличается от полученной в наименьшем числе символов. Такое декодирование называется декодированием по методу максимального правдоподобия [3, C.15]. 4 Задача 1. Для слов длины m = 3 в алфавите B = {0, 1} используются кодовые слова длины n = 4 (3, 4 – коды). Порождающая матрица (3,4) имеет вид: [[1,0,0,1],[0,1,0,1],[0,0,1,1]]. Какую по кратности ошибку может обнаружить этот код? Определите кодовое слово b для слова исходного сообщения a = 001. Какое кодовое слово b соответствует слову исходного сообщения a = 100. Какое кодовое слово b соответствует слову исходного сообщения a = 111. Решение Определите кодовое слово для слова исходного сообщения. b = aG = 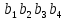 , где , где кодовое слово для слова исходного сообщения будет b= 0011 Какое кодовое слово соответствует слову исходного сообщения. где кодовое слово для слова исходного сообщения будет b = 1001 Какое кодовое слово соответствует слову исходного сообщения. где кодовое слово для слова исходного сообщения будет b = 1111 |
