Лекционный курс. Основы теплопередачи
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
ПРЕЗЕНТАЦИЯ ЛЕКЦИЙ: ОСНОВЫ ТЕПЛОПЕРЕДАЧИ Глава 1. Основные положения теплопроводности 1.1. Виды теплообмена 1.2. Основные понятия и определения 1.3. Основной закон теплопроводности 1.4. Дифференциальное уравнение теплопроводности 1.5. Краевые условия. Расчётное уравнение теплоотдачи Глава 2. Теплопроводность при стационарном режиме и граничных условиях первого рода 2.1. Теплопроводность через однослойную плоскую стенку 2.2. Теплопроводность через многослойную плоскую стенку 2.3. Теплопроводность через однослойную цилиндрическую стенку 2.4. Теплопроводность через многослойную цилиндрическую стенку 2.5. Теплопроводность через шаровую стенку 2.6. Теплопроводность тел различной формы Глава 3. Теплопроводность при стационарном режиме и граничных условиях третьего рода. Коэффициент теплопередачи 3.1. Передача теплоты через плоскую однослойную и многослойную стенки (теплопередача) 3.2. Передача теплоты через цилиндрическую однослойную и многослойную стенки 3.3. Критический диаметр изоляции 3.4. Передача теплоты через шаровую стенку 3.5. Передача теплоты через ребристую стенку 3.6. Интенсификация теплопередачи Глава 4. Конвективный теплообмен 4.1. Основы теории конвективного теплообмена: физические свойства жидкостей, режимы течения и пограничный слой 4.2. Основы теории подобия: числа подобия и теоремы подобия 4.3. Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду 4.4. Уравнения подобия Глава 5. Теплообмен излучением 5.1. Общие сведения о тепловом излучении 5.2. Основной закон поглощения 5.3. Теплообмен излучением между твердыми телами: параллельные пластины; теплообмен излучением между телами, одно из которых находится внутри другого; произвольно расположенные тела 5.4. Экраны 5.5. Излучение газов 5.6. Сложный теплообмен 5.7. Теплообмен излучением в котельных топках ГЛАВА 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕПЛОПРОВОДНОСТИ 1. 1. Виды теплообмена Процесс теплопередачи может осуществляться тремя способами. В связи с этим различают три основных вида теплообмена: теплопроводность; конвекция; лучистый теплообмен. Теплопроводность – это явление передачи энергии с помощью непосредственного взаимодействия атомов или молекул или путём диффузии свободных атомов или молекул. Конвекция – процесс переноса тепла движущимися частицами из одной точки пространства в другую. В идеальном случае при конвекции не может осуществляться передача тепла. Данный процесс характерен для жидких и газообразных сред. На основании этого для реальных процессов сложное совместное явление конвекции и теплопроводности получило название конвективного теплообмена. В зависимости от причины, вызывающей движение жидкости и газа, конвективный теплообмен подразделяют на два вида: конвективный теплообмен при свободном движении среды (сводная конвекция); конвективный теплообмен при вынужденном движении среды (вынужденная конвекция). Теплопередача, осуществляемая тепловым излучением, или лучистым теплообменом, характеризуется тем, что нагретое тело способно превращать часть энергии, принадлежащей телу, в лучистую энергию, которая передаётся от одного тела к другому. Встречая на своём пути какое-нибудь тело, тепловые лучи частично поглощаются и снова превращаются в теплоту, частично отражаются и частично проходят сквозь тело. Тепловые лучи подчиняются всем законам световых лучей: законам отражения, преломления и поглощения. 1. 2. Основные понятия и определения Теплообмен между стенкой и соприкасающейся с ней жидкостью (газом) носит название теплоотдачи. Тело, имеющее более высокую температуру Т1, называется теплоотдающим телом. Второе тело, имеющее более низкую температуру Т2, называется тепловоспринимающим телом. Количество тепла, проходящее через данную поверхность в единицу времени, называется тепловым потоком и обозначается Q (Вт). Тепловой поток, проходящий через единицу поверхности, называется удельным тепловым потоком и обозначается q(Вт/м2). Т 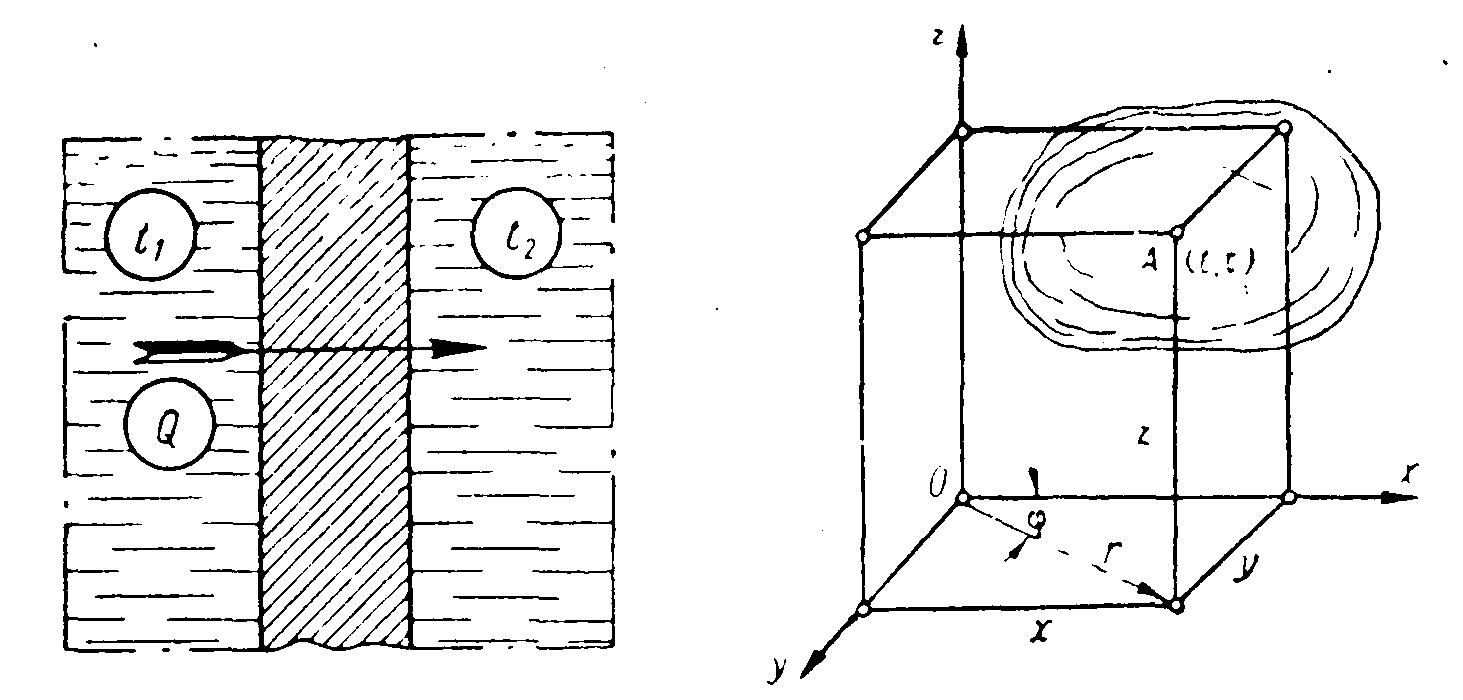 еплообмен между жидкостями (газами или газом и жидкостью), разделенными твердой стенкой, называется теплопередачей через стенку. еплообмен между жидкостями (газами или газом и жидкостью), разделенными твердой стенкой, называется теплопередачей через стенку. Температурным градиентом называется предел отношения – изменения температуры к расстоянию по нормали к изотермической поверхности при стремлении последнего к нулю. 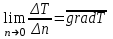 (2.7) (2.7)Температурный градиент есть вектор, направленный по нормали к изотермической поверхности в точке А. За положительное направление градиента принимают направление возрастания температур. Для разных точек, лежащих на одной и той же поверхности уровня, величина градиента неодинакова: она будет больше там, где меньше расстояние n между поверхностями уровня. 1. 3. Основной закон теплопроводности Количественная оценка тепла, проходящего внутри данного тела вследствие теплопроводности, базируется на гипотезе, высказанной в 1822 году французским ученым Фурье. По этой гипотезе элементарное количество тепла dQ, проходящее через элемент изотермической поверхности dF за промежуток времени d, пропорционально температурному градиенту  : :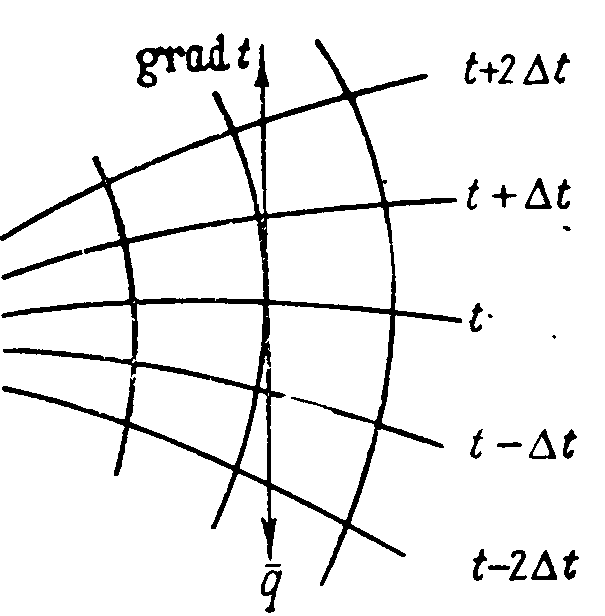 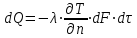 . .Если отнести количество тепла, переданное посредством теплопроводности, к единице изотермической поверхности и к единице времени, то получим удельный тепловой поток 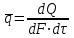 . .Вектор 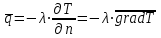 , ,называемый тепловым потоком, нормален к поверхности уровня и направлен в сторону убывания температуры. 1. 4. Дифференциальное уравнение теплопроводности 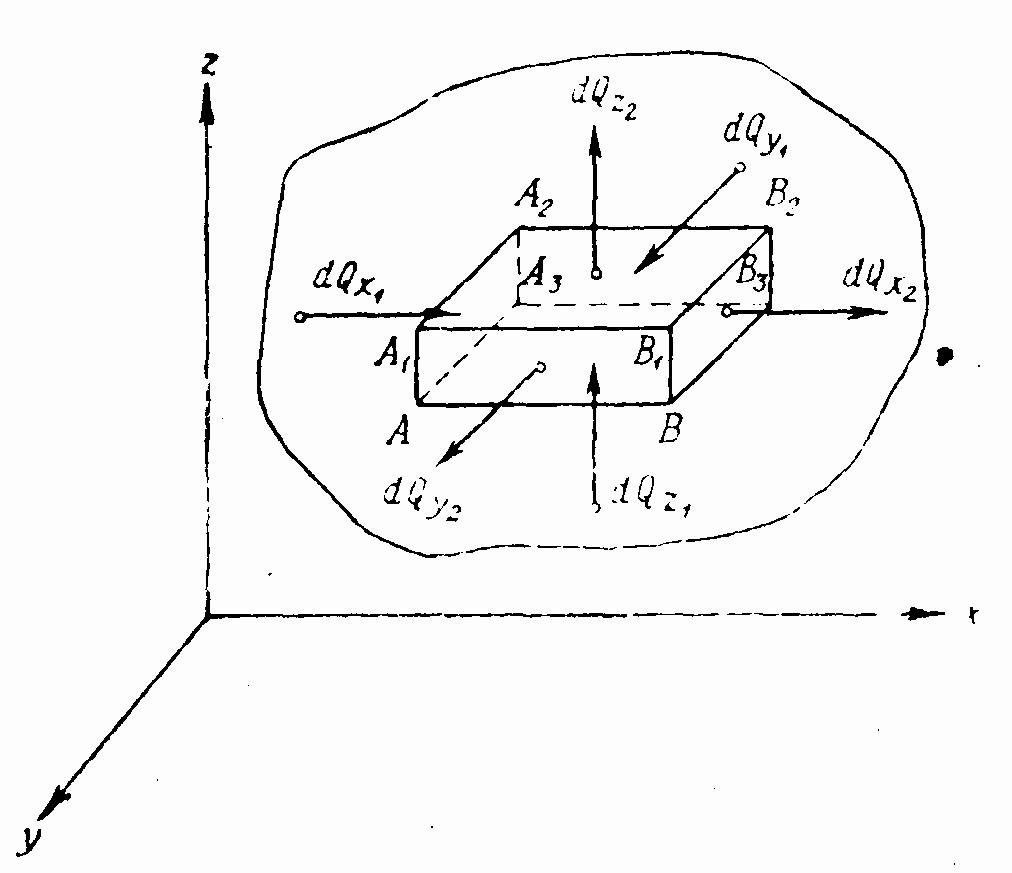 При решении всех без исключения задач теплопроводности как при стационарном, так и при нестационарном тепловом режимах, обязательным является знание поля температур. При выводе дифференциального уравнения теплопроводности будем считать, что физические параметры: (коэффициент теплопроводности), с (теплоемкость) и (удельный вес) не зависят от координат и времени в пределах всего поля. 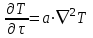 . . Уравнение называется основным дифференциальным уравнением теплопроводности. Оно устанавливает связь между временным и пространственным изменением температуры в любой точке поля. Величина  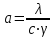 . . называется коэффициентом температуропроводности тела. 1. 5. Краевые условия. Расчетное уравнение теплоотдачи Основное дифференциальное уравнение теплопроводности характеризует пространственно-временное изменение температуры в любой точке поля, объединяя все без исключения явления теплопроводности независимо от геометрической формы тела, его физических свойств и условий взаимодействия с окружающей средой. Краевые граничные условия связаны с взаимодействием изучаемого тела с окружающей средой (например, распределение температур на поверхности тела для каждого момента времени). Граничные краевые условия в свою очередь могут быть заданы тремя способами: Граничное условие первого рода задается распределением температур по поверхности тела для любого момента времени. Граничное условие второго рода задается тепловым потоком в каждой точке поверхности тела для каждого момента времени. Граничное условие третьего рода заключается в задании температуры среды, окружающей изучаемое тело, и закона теплоотдачи между поверхностями и окружающей средой. 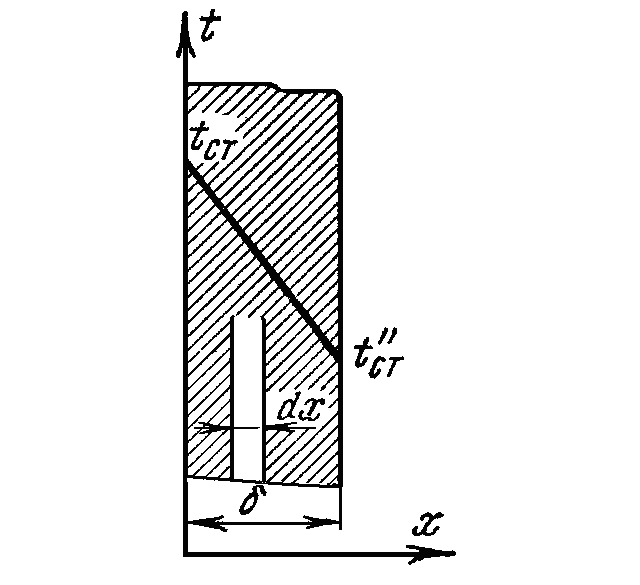 Глава 2. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ И ГРАНИЧНЫХ УСЛОВИЯХ ПЕРВОГО РОДА 2.1.Теплопроводность через однослойную плоскую стенку Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля. 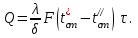 Количество теплоты, передаваемое теплопроводностью через плоскую стенку, прямо пропорционально коэффициенту теплопроводности стенки 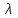 ее площади ее площади 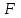 , промежутку времени , промежутку времени 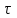 , разности температур на наружных поверхностях стенки , разности температур на наружных поверхностях стенки 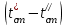 и обратно пропорционально толщине стенки и обратно пропорционально толщине стенки 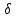 . . Тепловой поток зависит не от абсолютного значения температур, а от их разности 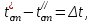 называемой температурным напором. называемой температурным напором.2.2. Теплопроводность через многослойную плоскую стенку Расчетную формулу теплопроводности сложной стенки при стационарном состоянии можно вывести из уравнения теплопроводности для отдельных слоев, считая, что тепловой поток, проходящий через любую изотермную поверхность неоднородной стенки, один и тот же. 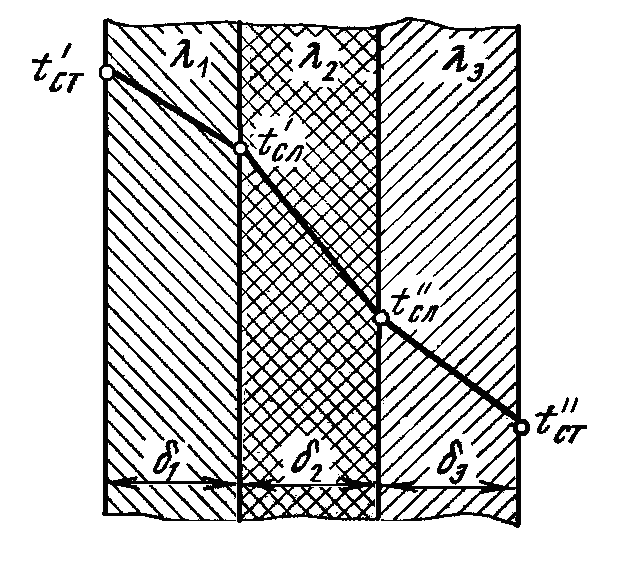 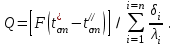 Отношение 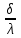 называют термическим сопротивлением слоя, а величину называют термическим сопротивлением слоя, а величину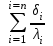 — полным термическим сопротивлением многослойной плоской стенки. — полным термическим сопротивлением многослойной плоской стенки.2.3. Теплопроводность через однослойную цилиндрическую стенку В 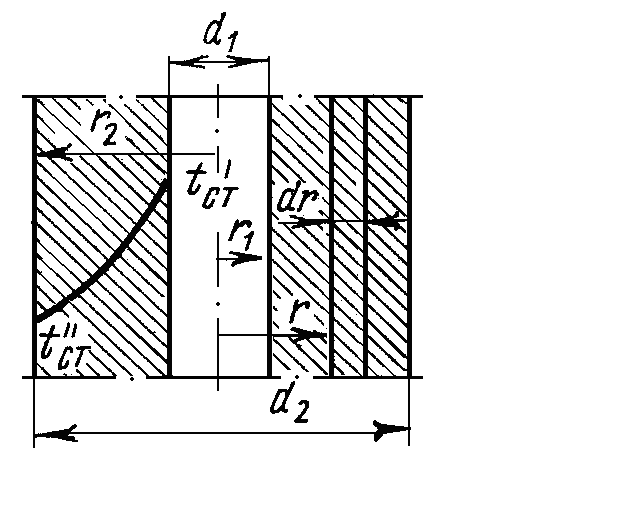 нешняя и внутренняя поверхности прямой цилиндрической трубы поддерживаются при постоянных температурах нешняя и внутренняя поверхности прямой цилиндрической трубы поддерживаются при постоянных температурах 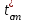 и и 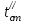 . . Изотермные поверхности будут цилиндрическими поверхностями, имеющими общую ось с трубой. Температура будет меняться только в направлении радиуса, благодаря этому и поток теплоты будет тоже радиальным. Труба имеет бесконечную длину. Температурное поле в этом случае будет одномерным. 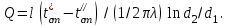 Как видно из уравнения, распределение температур в стенке цилиндрической трубы представляет собой логарифмическую кривую. Тепловой поток, проходящий через цилиндрическую стенку, определяется заданными граничными условиями и зависит от отношения наружного диаметра к внутреннему. 2.4. Теплопроводность через многослойную цилиндрическую стенку 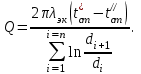 Величина эквивалентного коэффициента теплопроводности для цилиндрической стенки определяется так же, как и для плоской. 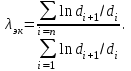 2.5. Теплопроводность через шаровую стенку Постоянный тепловой поток направлен через шаровую стенку, причем источник теплоты находится внутри шара. Температура изменяется только по направлению радиуса. Изотермные поверхности представляют собой концентрические шаровые поверхности. Температура внутренней поверхности 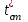 , наружной , наружной 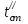 ; коэффициент теплопроводности стенки ; коэффициент теплопроводности стенки 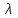 — величина постоянная. Внутренний радиус шара — величина постоянная. Внутренний радиус шара 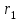 ,наружный — ,наружный — 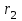 . .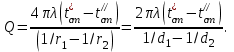 2.6. Теплопроводность тел произвольной формы Количество теплоты, проходящее через стенки тел неправильной формы (например, стенка не плоская, а ограничена кривыми поверхностями, или когда поверхность не цилиндрическая, а овальная), можно определить по следующему уравнению: 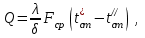 где 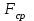 — поверхность, которую находят в зависимости от формы тела. — поверхность, которую находят в зависимости от формы тела.Г 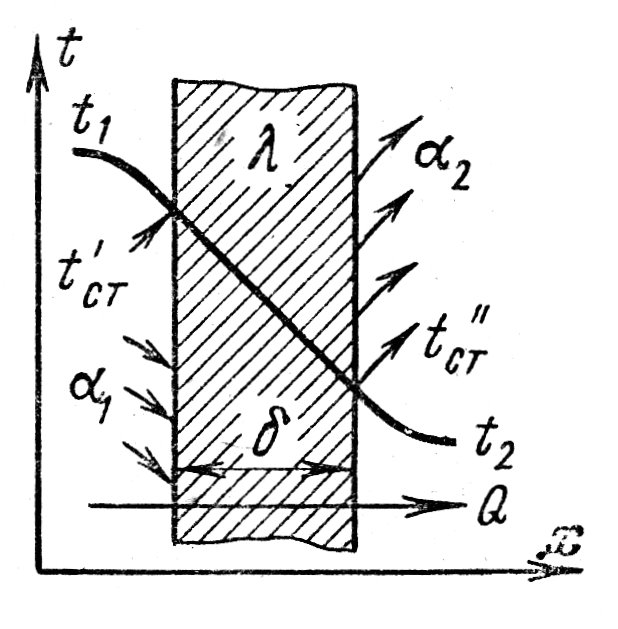 ЛАВА 3. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ ЛАВА 3. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕИ ГРАНИЧНЫХ УСЛОВИЯХ ТРЕТЬЕГО РОДА, КОЭФФИЦИЕНТ ТЕПЛОПЕРЕДАЧИ 3. 1. Передача теплоты через плоскую однослойную и многослойную стенки (теплопередача) Перенос теплоты от одной подвижной среды (горячей) к другой (холодной) через однослойную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача представляет собой весьма сложный процесс, в котором теплота передается всеми способами: теплопроводностью, конвекцией и излучением. Величина 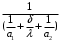 обозначается буквой к, имеет размерность вт/(м2-град) и называется коэффициентом теплопередачи. обозначается буквой к, имеет размерность вт/(м2-град) и называется коэффициентом теплопередачи.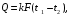 или 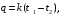 Числовое значение коэффициента теплопередачи выражает количество теплоты, проходящей через единицу поверхности стенки в единицу времени от горячего к холодному теплоносителю при разности температур между ними в 1°. 3. 2. Передача теплоты через цилиндрические однослойную и многослойную стенки 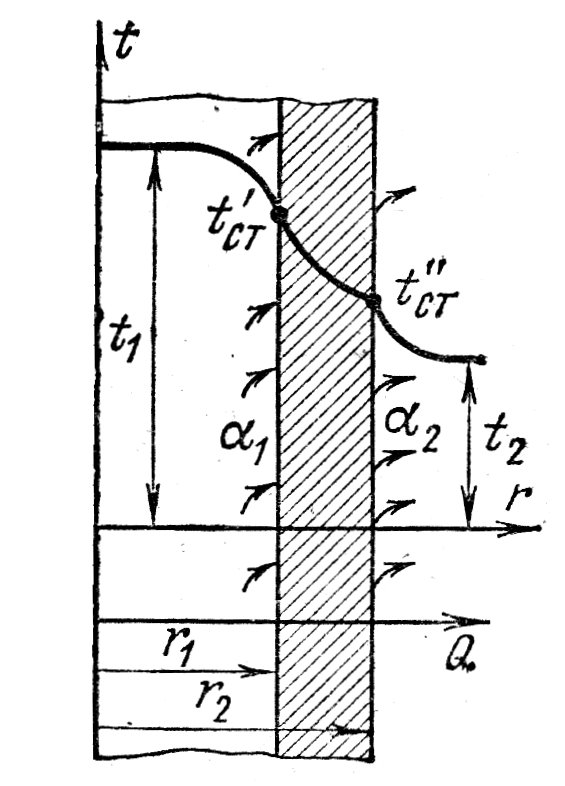 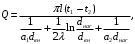 где 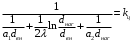 называют линейным коэффициентом теплопередачи, имеющим размерность вт/(м*град). 3. 3. Критический диаметр изоляции Тепловой изоляцией называют всякое покрытие горячей поверхности, которое способствует снижению потерь теплоты в окружающую среду. 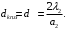 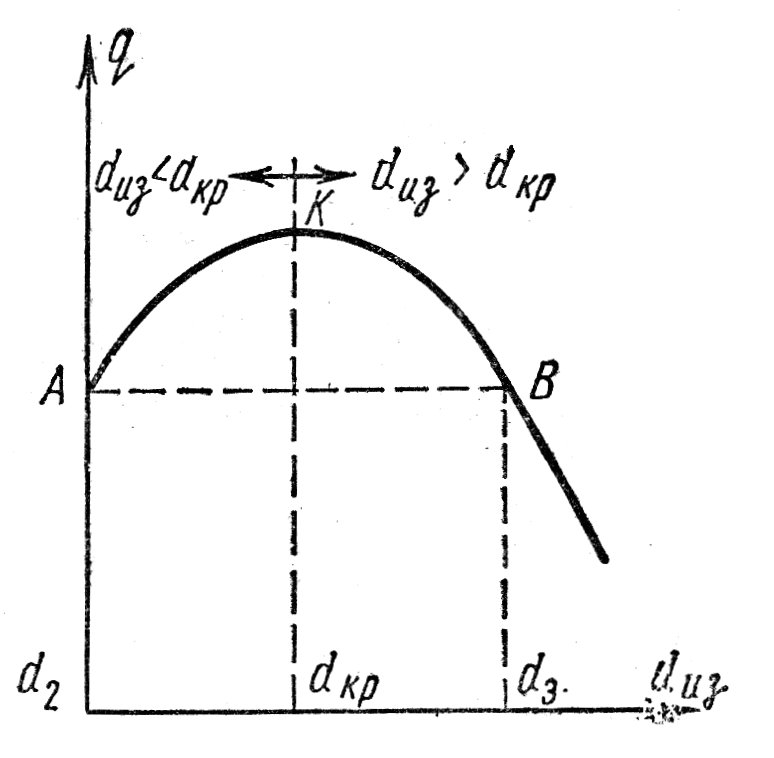 Из уравнения следует, что критический диаметр изоляции не зависит от размеров трубопровода. Он будет тем меньше, чем меньше коэффициент теплопроводности изоляции и чем больше коэффициент теплоотдачи а2от наружной поверхности изоляции к окружающей среде. 3. 4. Передача теплоты через шаровую стенку 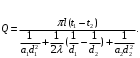 Определяем коэффициент теплопередачи для шаровой стенки: 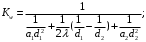 имеет размерность вт/град. Обратную величину: 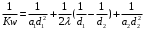 называют общим термическим сопротивлением шаровой стенки. 3. 5. Передача теплоты через ребристую стенку О 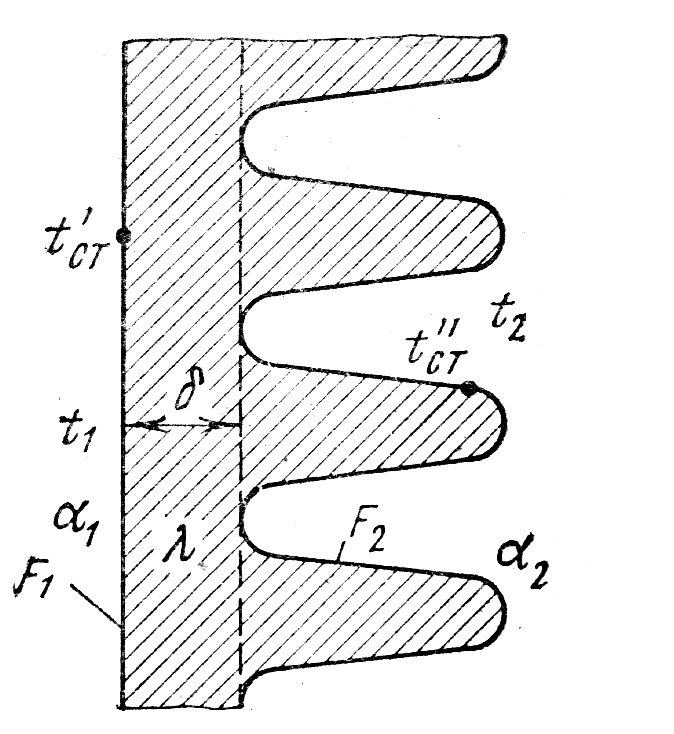 тношение количества теплоты Qp, передаваемой поверхностью ребер в окружающую среду, к теплоте Qn.v, которую эта поверхность могла бы передать при постоянной температуре, равной температуре у основания ребер, называется коэффициентом эффективности ребер: тношение количества теплоты Qp, передаваемой поверхностью ребер в окружающую среду, к теплоте Qn.v, которую эта поверхность могла бы передать при постоянной температуре, равной температуре у основания ребер, называется коэффициентом эффективности ребер: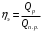 . .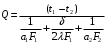 или 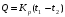 откуда коэффициент теплопередачи для ребристой стенки равен 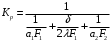 kp имеет размерность вт/град. 3. 6. Интенсификация теплопередачи Практика эксплуатации тепловых аппаратов требует наилучших условий передачи теплоты от горячего теплоносителя к холодному. Эти условия главным образом зависят от коэффициента теплопередачи. Однако знания численного значения одного коэффициента теплопередачи для исследования процесса теплопередачи недостаточно. Только анализ соотношений всех термических сопротивлений дает возможность сделать правильное заключение и позволяет существенно изменить величину теплового потока. ГЛАВА 4. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН 4. 1. Основы теории конвективного теплообмена П 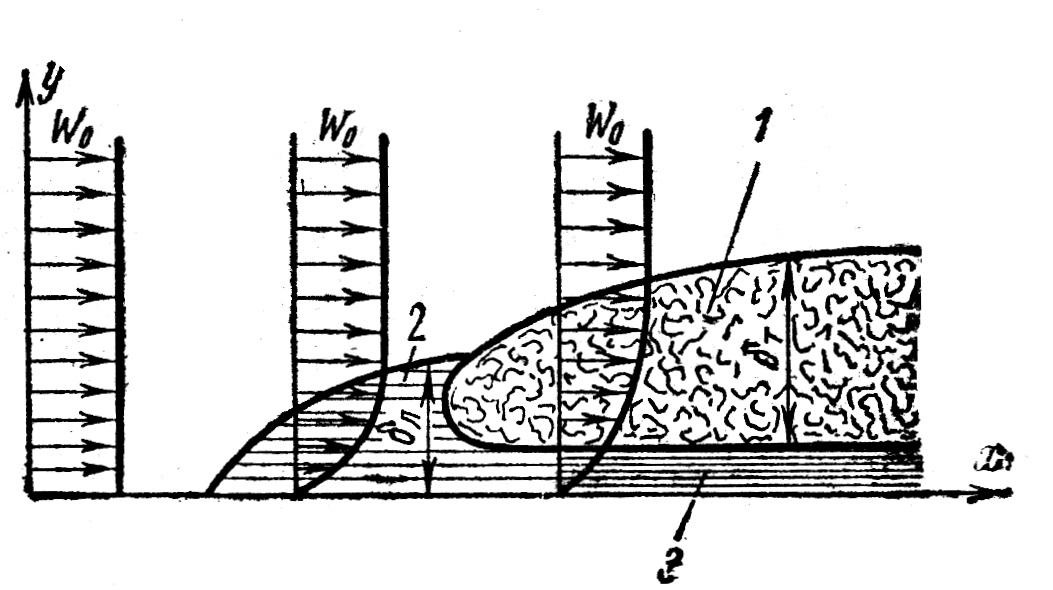 ередача теплоты конвекцией, всегда связана с теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом. ередача теплоты конвекцией, всегда связана с теплопроводностью. Совместный процесс конвекции и теплопроводности называется конвективным теплообменом.Различают конвекцию вынужденную (движение жидкости создается искусственно) и свободную — движение возникает в связи с ее нагреванием и изменением плотности. Жидкость движется спокойно, без пульсаций, образуя струи, следующие очертаниям канала. Движение такого рода называется ламинарным. Второй вид потока называется турбулентным, в нем непрерывно происходит перемешивание всех слоев жидкости. Каждая частица потока, перемещаясь вдоль канала с некоторой скоростью, совершает различные движения перпендикулярно стенкам канала. 4. 2. Коэффициент теплоотдачи. Дифференциальное уравнение теплообмена 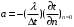 Дифференциальное уравнение описывает процесс теплообмена на поверхности канала (п= 0). Система дифференциальных уравнений состоит из уравнений энергии (или теплопроводности), теплообмена, движения и сплошности. Дифференциальное уравнение энергии устанавливает связь между пространственным и временным изменением температуры в любой точке движущейся жидкости: 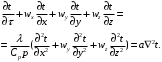 Если wx= wy = wz= 0, уравнение энергии переходит в уравнение теплопроводности для твердых тел (если отсутствуют внутренние источники теплоты). Дифференциальное уравнение теплообмена выражает условия теплообмена на границе твердого тела и жидкости: 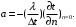 Дифференциальное уравнение движения вязкой несжимаемой жидкости представлено уравнением Навье - Стокса: для оси х 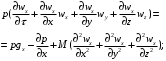 Дифференциальное уравнение сплошности, или непрерывности, для сжимаемых жидкостей имеет вид: 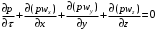 . .Для несжимаемых жидкостей при р = const уравнение сплошности принимает вид 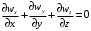 . .4. 3. Основы теории подобия Любое дифференциальное уравнение (или система уравнений) является математической моделью целого класса явлений. Следовательно, под классом понимается такая совокупность явлений, которая характеризуется одинаковым механизмом процессов и одинаковой физической природой. Чтобы получить из множества решений одно частное, надо знать все характерные особенности данного явления, выделяющие его из всего класса однородных явлений. Эти дополнительные условия, которые вместе с дифференциальным уравнением однозначно определяют единичное явление, называют условиями однозначности. Условия однозначности должны содержать все особенности данного конкретного явления. 4. 4. Числа подобия Константы подобия имеют одинаковое значение для конечных и бесконечно малых величин. Равенство можно представить в виде: 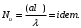 Если имеется отношение двух каких-либо однородных величин, то оно называется симплексом. Однородными называют физические величины, имеющие одинаковое физические содержание и размерность. 4. 5. Теоремы подобия Первая теорема может быть сформулирована еще и так: у подобных явлений числа подобия численно одинаковы. Вторая теорема подобия гласит: если физическое явление описывается системой дифференциальных уравнений, то всегда существует возможность представления их в виде уравнений подобия, или интеграл дифференциального уравнения (или системы уравнений) может быть представлен как функция чисел подобия дифференциального уравнения. Вторая теорема утверждает, что операция интегрирования не из: меняет вида чисел подобия. Третья теорема исходит из предположения, что явления протекают в геометрически подобных системах (поэтому геометрическое подобие систем есть первое необходимое условие для существования подобия), что для рассматриваемого явления можно составить дифференциальные уравнения, что установлено существование и единственность решения уравнения при заданных граничных условиях, что известны численные значения коэффициентов и физических параметров, входящих в дифференциальное уравнение. 4. 6. Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду 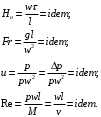 где Но — число подобия гидродинамической гомохронности, характеризующее скорость изменения поля скоростей движущейся жидкости во времени; Fr — число Фруда, определяющее отношение сил инерции к силам тяжести; Еи — число Эйлера, характеризующее соотношение между силами давления и силами инерции; Re — число Рейнольдса, представляющее собой отношение сил инерции к силам вязкости и определяющее характер течения жидкости. 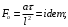 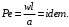 где Fo — число Фурье, критерий тепловой гомохронности, характеризующее связь между скоростью изменения температурного поля, физическими параметрами и размерами тела; Ре — число Пекле, число подобия конвективного теплообмена. 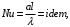 где Nu — число Нуссельта, характеризующее конвективный теплообмен между жидкостью и поверхностью твердого тела. 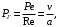 где Рг — число Прандтля, определяющее физические свойства жидкости. 4. 7. Уравнения подобия Уравнением подобия называют зависимость между каким-либо определяемым числом подобия и другими определяющими числами подобия. Академик М. А. Михеев рекомендует учитывать направление теплового потока отношением Ргж/Ргст в степени 0,25. Тогда общее уравнение подобия для конвективного теплообмена принимает следующий вид: 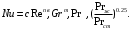 ГЛАВА 5. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ 5. 1. Общие сведения о тепловом излучении В зависимости от длины волны А, лучи обладают различными свойствами. Из всех лучей наибольший интерес для теплопередачи представляют тепловые лучи с 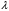 = 0,8-40 мкм. = 0,8-40 мкм.Каждое тело способно не только излучать, но и отражать, поглощать и пропускать через себя падающие лучи от другого тела. Если обозначить общее количество энергии излучения, падающей на тело, через Q, то часть энергии, равная А, поглотится телом, часть, равная R, отразится, а часть, равная D, пройдет сквозь тело. Отсюда 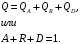 Величину А называют поглощательной способностью. Она представляет собой отношение поглощенной энергии излучения ко всей энергии излучения, падающей на тело. Величину Rназывают отражательной способностью. Rесть отношение отраженной энергии излучения ко всей падающей. Величину Dназывают пропускательной способностью. Dесть отношение прошедшей сквозь тело энергии излучения ко всей энергии излучения, падающей на тело. 5. 2. Основной закон поглощения Падение интенсивностипропорционально начальной интенсивности , пути dxи зависит от свойств тела: 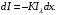 Знак минус в правой части указывает на убывание интенсивности. Коэффициент пропорциональности k, зависящий от физических свойств тела, температуры и длины волны, называется коэффициентом абсорбции, или коэффициентом поглощения вещества, для лучей с данной длиной волны; k имеет размерность Им. Коэффициент поглощения 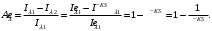 5. 3. Основные законы теплового излучения Закон Планка. Планк теоретически, исходя из электромагнитной природы излучения и используя представление о квантах энергии, установил следующий закон изменения интенсивности излучения абсолютно черного тела в зависимости от температуры и длины волны: 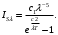 где е — основание натуральных логарифмов; с1 =3,74*10-16 вт-м2— первая постоянная Планка; с2= 1,44*10-2 м*град — вторая постоянная Планка; 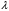 - длина волны, Т — температура излучающего тела, °К. - длина волны, Т — температура излучающего тела, °К.Закон Стефана — Больцмана. 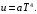 Уравнение является аналитическим выражением закона Стефана - Больцмана, т. е. объемная плотность энергии равновесного излучения пропорцональна абсолютной температуре в четвертой степени. Обычно в технической литературе закон Стефана — Больцмана пишут в следующем виде: 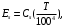 где Сs— коэффициент излучения абсолютно черного тела: Закон Кирхгофа. Для всякого тела энергия излучения и энергия поглощения зависят от температуры и длины волны. Различные тела имеют различные значения Е и А. Зависимость между ними устанавливается законом Кирхгофа. 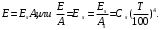  . .Из закона Кирхгофа следует, что если тело обладает малой поглощательной способностью, то оно одновременно обладает и малой излучательной способностью (полированные металлы). Абсолютно черное тело, обладающее максимальной поглощательной способностью, имеет и наибольшую излучательную способность. 5. 4. Теплообмен излучением между твердыми телами. Параллельные пластины Сумма собственного и отраженного излучений, испускаемых поверхностью данного тела, называется эффективным (фактическим) излучением:  Таким образом, тепловое излучение между параллельными поверхностями определяется уравнением  где  - приведенный коэффициент излучения. - приведенный коэффициент излучения.5. 5. Теплообмен излучением между телами, одно из которых находится внутри другого 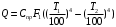 . .5. 6. Произвольно расположенные тела 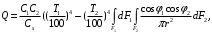 где 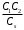 приведенный коэффициент излучения данной системы тел; приведенный коэффициент излучения данной системы тел; 5. 7. Экраны 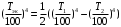 5. 8. Излучение газов 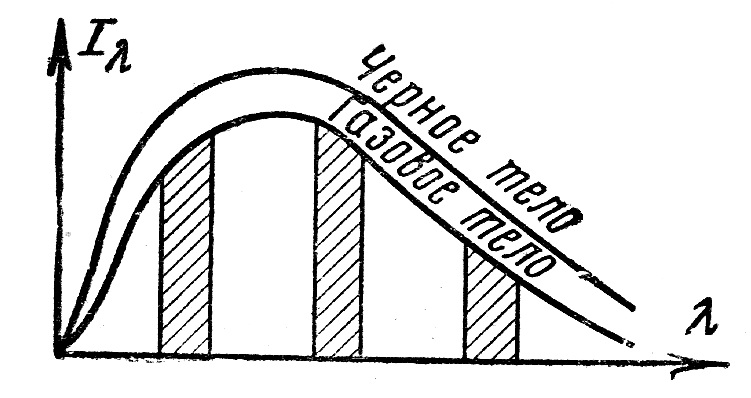 Излучение газообразных тел резко отличается от излучения твердых тел. Одноатомные и двухатомные газы обладают ничтожно малой излучательной и поглощательной способностью. Эти газы считаются прозрачными для тепловых лучей. Трехатомные (С02 и Н20 и др.) и многоатомные газы уже обладают значительной излучательной, а следовательно, и поглощательной способностью. 5. 9. Сложный теплообмен Теплообмен, учитывающий все виды теплообмена, называется сложным теплообменом. Количественной характеристикой процесса теплообмена от газа к стенке (или наоборот) является суммарный коэффициент теплоотдачи: 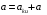 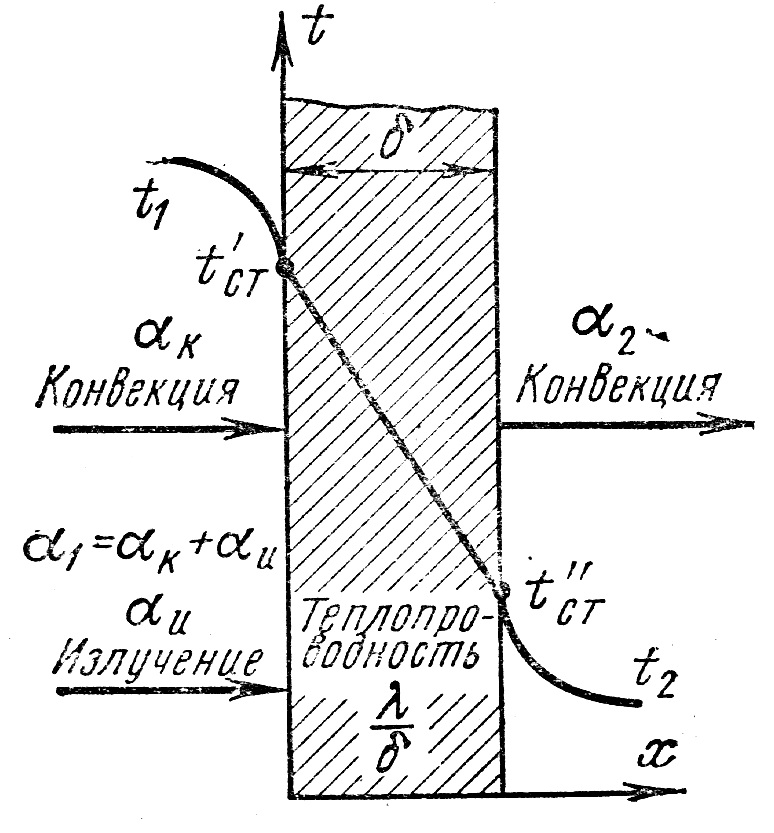 где аk учитывает передачу теплоты теплопроводностью и конвекцией, а аи - передачу теплоты излучением. Плотность теплового потока рассчитываемого аппарата определяется по уравнению 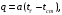 где а - суммарный коэффициент теплоотдачи входит в уравнение коэффициента теплопередачи. В этом случае уравнение коэффициента теплопередачи для плоской стенки принимает вид 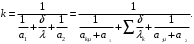 5. 10. Теплообмен излучением в котельных топках Сгорание топлива в топочных устройствах сопровождается образованием газов с высокой температурой, которые могут передавать излучением большое количество теплоты. Поэтому роль лучистого теплообмена в топках современных котлов весьма велика и общая передача теплоты излучением на стенки котельных труб доходит до 50% и больше от всей теплоты, выделяемой при сгорании топлива. Лучистый теплообмен в топках по своей интенсивности во много раз превышает конвективный теплообмен при средних скоростях перемещения газов. Советскими теплотехниками были разработаны методы расчетов теплопередачи в котельных топках, основанные на большом экспериментальном материале, и предложены практические расчеты топок по эмпирическим формулам (В. Н. Тимофеев, А. М. Гурвич и др.). Обычно расчет топки заключается в определении температуры дымовых газов на выходе из камеры горения котла. В 1949 г. в Энергетическом институте АН СССР его сотрудниками, проф. Г. Л. Поляк и С. Н. Шориным, была предложена сравнительно простая формула для расчета этой температуры: 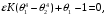 где 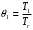 - безразмерная температура дымовых газов на выходе из топки; Т1 - температура дымовых газов на выходе из топки, °К; Т2 - теоретическая температура горения топлива, °К; - безразмерная температура дымовых газов на выходе из топки; Т1 - температура дымовых газов на выходе из топки, °К; Т2 - теоретическая температура горения топлива, °К; 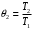 - безразмерная температура котельной стенки; Т2 - температура стенок топки, °К; - безразмерная температура котельной стенки; Т2 - температура стенок топки, °К;  - условный коэффициент черноты излучения в топочной камере, учитывающий все особенности теплообмена излучением движущейся, горящей и излучающей среды, усреднение температуры и конвективный теплообмен со стенками; - условный коэффициент черноты излучения в топочной камере, учитывающий все особенности теплообмена излучением движущейся, горящей и излучающей среды, усреднение температуры и конвективный теплообмен со стенками;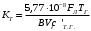 - топочный критерии, - топочный критерии,где FЛ - тепловоспринимающая поверхность стенок топки; В - часовой расход топлива; VГ— количество получаемых продуктов сгорания, м3/кг; с’Т.Г. - средняя объемная теплоемкость продуктов сгорания в интервале температур (ТГ - Т1). |
