квадратичные формы и квадрики. реферат. Основная часть. 4 I. Квадратичные формы.
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
1 2 II. Квадрики.1. Определения. Примеры.Квадрикой(гиперповерхностью второго порядка) в аффинном пространстве An называется множество точек, координаты которых в некоторой аффинной системе координат удовлетворяют уравнению второй степени. В общем виде уравнение квадрики может быть записано следующим образом где Пример 1. В A2 квадрика имеет уравнение вида И является кривой 2-го порядка. Пример 2. В A3 квадрика – поверхность 2-го порядка: Понятие квадрики не зависит от выбора системы координат. Может случиться, что над полем действительных чисел R для некоторого уравнения (20) нет ни одной удовлетворяющей ему точки. Всё-таки про такое уравнение говорят, что оно есть уравнение квадрики. Иногда при этом гиперповерхность называют мнимой(или нулевой). Например, говорят, что уравнение Теорема. Если множество точек в некоторой аффинной системе координат определяется уравнением второй степени, то оно будет определяться уравнением второй степени и в любой другой аффинной системе координат. Доказательство. Если множество точек задано в старой системе координат уравнением (20), то для получения уравнения данного множества в новой системе достаточно подставить в это уравнение выражения старых координат Степень уравнения не может и понизиться. Действительно, если бы степень нового уравнения оказалась ниже второй, то при обратном переходе от этого уравнения к уравнению (20) степень уравнения стала бы равной двум, т.е. повысилась; но выше уже было доказано, что это невозможно. 2. Приведение уравнения квадрики к нормальному виду.Пусть квадрика задана в некоторой аффинной системе координат уравнением (20). Поставим себе цель – упростить это уравнение путем надлежащего выбора новой аффинной системы координат. Теорема. При соответствующем выборе аффинной системы координат уравнение любой квадрики может быть приведено к одному из следующих видов где где где Доказательство. Вначале произведем линейное преобразование С геометрической точки зрения это означает переход к новой аффинной системе координат с прежним началом. При соответствующей нумерации новых координат уравнение (20) квадрики примет вид Выделяя полные квадраты, будем иметь 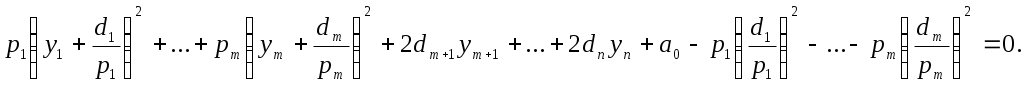 Подвергнем систему координат параллельному переносу Подвергнем систему координат параллельному переносу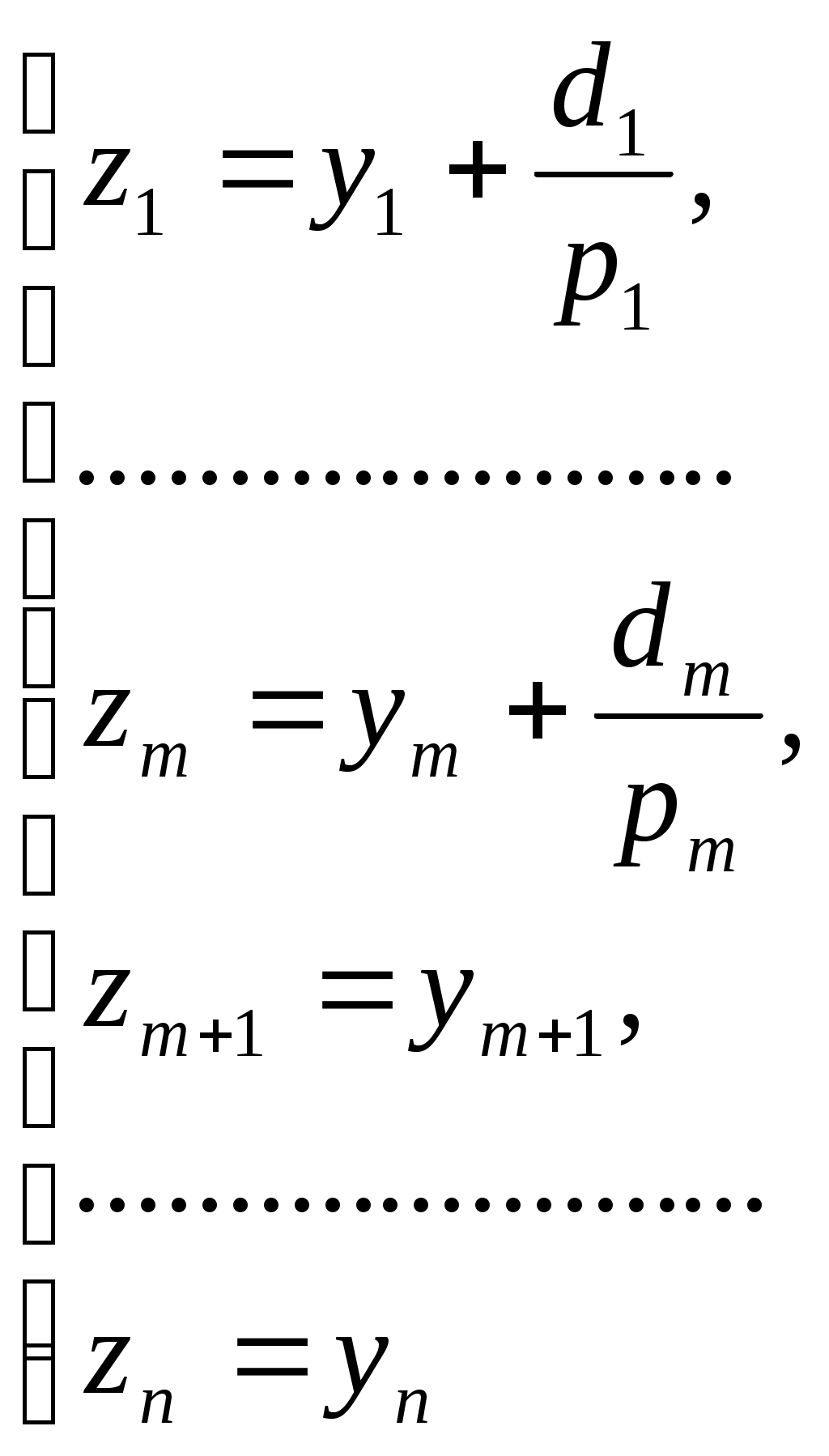 Если ввести обозначение 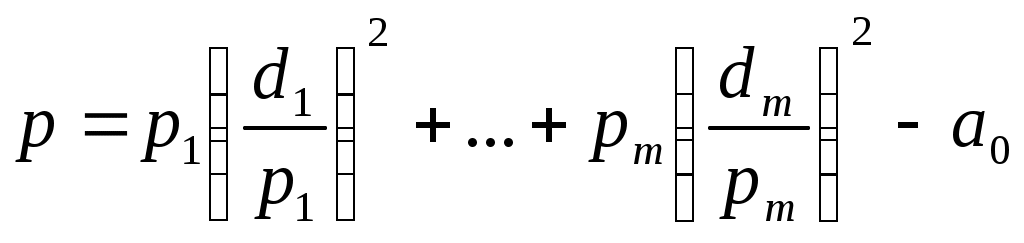 то относительно полученной системы координат квадрика будет иметь уравнение Заметим, что при m=n формулы параллельного переноса принимают вид а уравнение (24) – вид Продолжим упрощение уравнения квадрики. Возможны следующие случаи: 1) Если в уравнении (24) Перейдя к новой системе координат по формулам 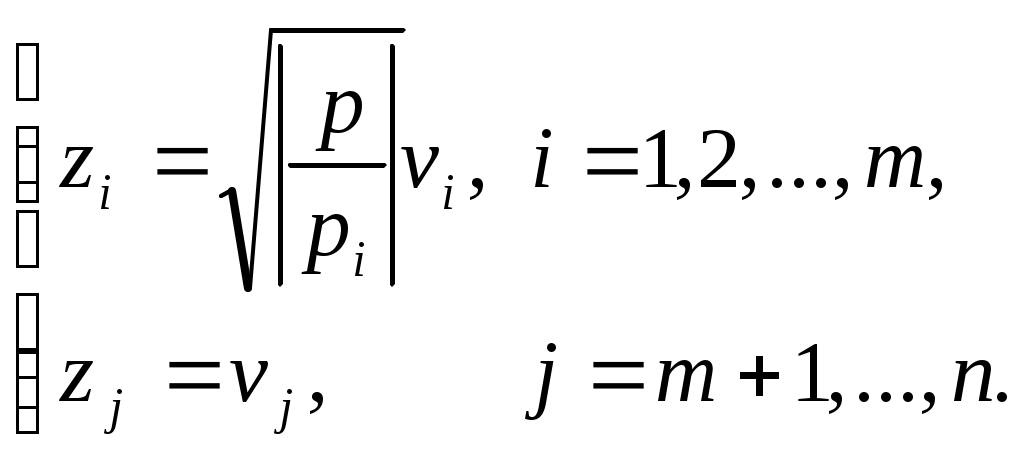 Приведем уравнение квадрики к виду где 2) если После преобразования координат по формулам 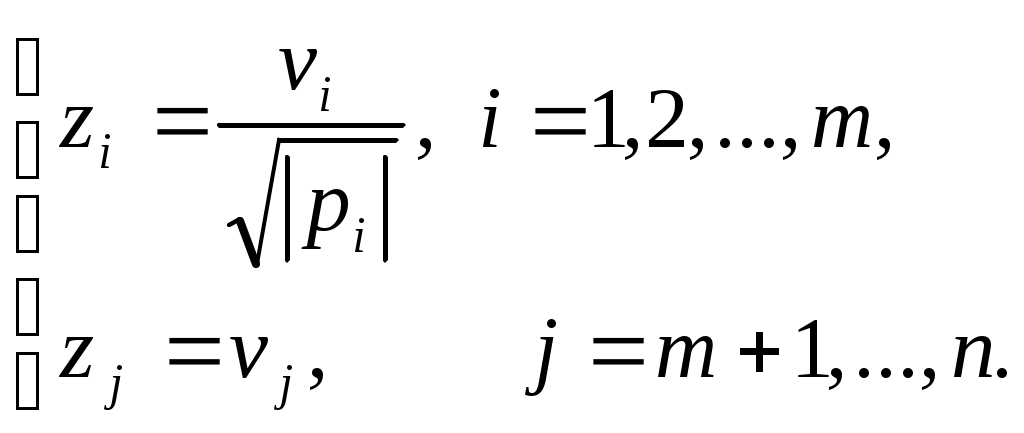 будем иметь где 3) пусть теперь m<n и хотя бы один из коэффициентов 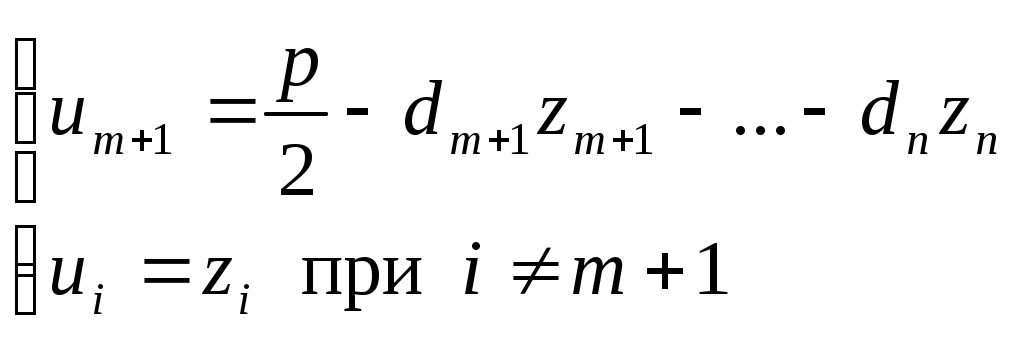 приведем уравнение (24) к виду После преобразования координат по формулам 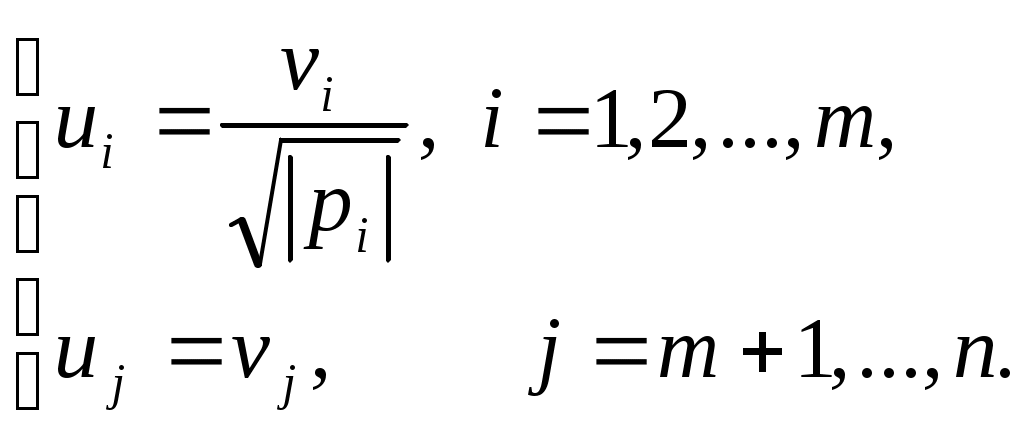 получим уравнение где Теорема доказана полностью. Уравнения (21), (22), (23) называются нормальными видами уравнения квадрики. 3. Центр квадрики.Определение. Точка S называется центром симметрии или просто центром квадрики, если точка, симметричная любой точке квадрики относительно S, также принадлежит квадрике. Теорема. Если уравнение квадрики имеет вид (21) или (22), то точка Доказательство. Если точки откуда Т.к. s1= s2=…= sm=0, то Уравнения (21) и (22) содержат координаты точки только во второй степени; следовательно, если координаты точки M' удовлетворяют какому-либо из этих уравнений, то этому же уравнению удовлетворяют координаты точки M''. Т.к. точка M'' симметрична точке M' относительно S, то S – центр квадрики. Из теоремы следует, что все точки (nm)-мерной плоскости, имеющей уравнения являются центрами квадрики (21) и (22); можно доказать, что других центров квадрика не имеет. В частности, при m=n эта плоскость является нуль-мерной: уравнениям (15) удовлетворяют координаты единственной точки – начала координат. В этом случае квадрика имеет единственный центр. Можно доказать, что квадрика (23) не имеет ни одного центра. Т.к. уравнение квадрики всегда может быть приведено к виду (21), (22) или (23), то для любой квадрики имеет место один и только один из следующих трех случаев: 1) квадрика не имеет центра; 2) квадрика имеет единственный центр (тогда она называется центральной); 3) квадрика имеет бесконечное множество центров, являющееся некоторой плоскостью. 4. Аффинная классификация квадрик.1. Эллипсоиды и гиперболоиды. При m=n уравнение (21) имеет вид где В зависимости от знаков 1) при Внешне это уравнение напоминает уравнение сферы евклидова пространства в прямоугольной декартовой системе координат, однако следует помнить, что мы пользуемся единой системой координат, а понятие сферы в аффинной геометрии отсутствует. 2) при Т.к. мы рассматриваем действительное аффинное пространство, то точек с координатами, удовлетворяющими этому уравнению, не существует. Однако по аналогии с предыдущим случаем это уравнение называют уравнением мнимого эллипсоида. 3) если Таким образом, эллипсоид и гиперболоид являются центральными квадриками. Конусы. При m=n уравнение (22) имеет вид где 1) Если знаки Если координаты точки А(а1, а2,…,аn), отличной от вершины конуса, удовлетворяют уравнению (27), то этому уравнению удовлетворяют и координаты любой точки вида (tа1, tа2,…,tаn). Множество всех таких точек является прямой, проходящей через А и вершину конуса – начало координат. Эта прямая целиком принадлежит конусу и называется его прямолинейной образующей. 2) Если 3. Параболоиды. При m=n1 уравнение (23) принимает вид где Квадрика в этом случае называется параболоидом. Параболоид не имеет центра. 4. Цилиндрические квадрики. Если в уравнениях (21) и (22) m<n, а в уравнении (23) m<n1, то, полагая в (21) и (22) m=r, а в (23) m=r1, получим соответственно где r<n и Квадрика, для которой (29), (30) или (31) является нормальным уравнением, называется цилиндрической. Можно показать, что цилиндрическая квадрика состоит из параллельных друг другу (nr)-мерных плоскостей (образующих), пересекающих некоторую квадрику (направляющую), лежащую в r-мерной плоскости. Квадрики (29) и (30) имеют в общем случае бесконечное множество центров, являющееся (nr)-мерной плоскостью. Квадрика (31) центров не имеет. Аффинная классификация квадрик в пространстве А2. Уравнение любой квадрики может быть приведено к одному из следующих нормальных видов: а) неконические центральные кривые: 1) 2) 3) б) конические центральные кривые: 4) 5) в) нецентральные нецилиндрические кривые: 6) г) цилиндрические кривые, имеющие центры: 7) 8) 9) Любые две квадрики, принадлежащие к одному и тому же классу, аффинно эквивалентны. Это связано с тем, что формулы перехода от одной аффинной системы координат к другой и формулы аффинных преобразований с алгебраической точки зрения имеют один и тот же вид. Заметим, что квадрики с различными нормальными уравнениями могут оказаться одинаковыми точечными множествами. Так, например, мнимый эллипс и пара мнимых параллельных прямых – пустое точечное множество. Поэтому квадрики, принадлежащие различным классам, иногда могут оказаться аффинно эквивалентными; с геометрической точки зрения эти классы тогда не различаются между собой. 5. Квадрики в Евклидовом пространстве.Упрощение уравнения квадрики производится вначале по тому же плану, что и в п. II.2, с той лишь разницей, что квадратичная форма, содержащаяся в левой части уравнения (20), приводится к каноническому виду с помощью ортогонального преобразования (а не произвольного линейного, как раньше). С геометрической точки зрения это означает переход к новой прямоугольной декартовой системе координат, получаемой из исходной прямоугольной декартовой системы координат с помощью вращения вокруг начала координат. Подвергая затем полученную систему координат параллельному переносу, приведем уравнение квадрики к где mn и коэффициенты При дальнейшем упрощении уравнения квадрики обычно уже не удается добиться того, чтобы все коэффициенты при квадратах координат были равны +1 или 1. Это связано с тем, что при помощи ортогонального преобразования квадратичная форма не всегда приводится к нормальному виду. Поэтому в пространстве Еn уравнение квадрики в общем случае уже не удается привести к такому же простому виду, как в пространстве Аn. Так как конгруэнтные фигуры являются также и аффинно эквивалентными, то аффинная классификация квадрик, установленная в п. II.4, остается в силе и для пространства Еn. Однако не всякие аффинно эквивалентные фигуры конгруэнтны; поэтому каждый из классов аффинной классификации может быть разбит на бесконечное множество классов так, что любые две квадрики из одного класса конгруэнтны, а любые две квадрики из разных классов не конгруэнтны. В связи с этим появляется возможность выделения новых видов квадрик, не рассматривавшихся в Аn. 6. Классификация квадрик в трёхмерном евклидовом пространстве. Классификация квадрик в пространстве Е2 совпадает с приведённой ранее классификацией в пространстве А2. Чтобы дать полную классификацию квадрик при п = 3, рассмотрим все частные случаи, которые могут представиться при упрощении уравнения (32). Случай 1. В зависимости от знаков 1) 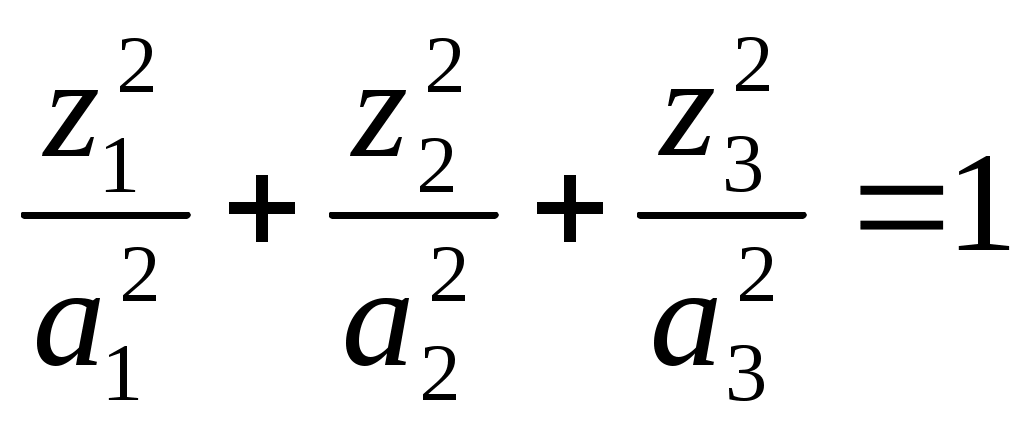 эллипсоид; эллипсоид;2) 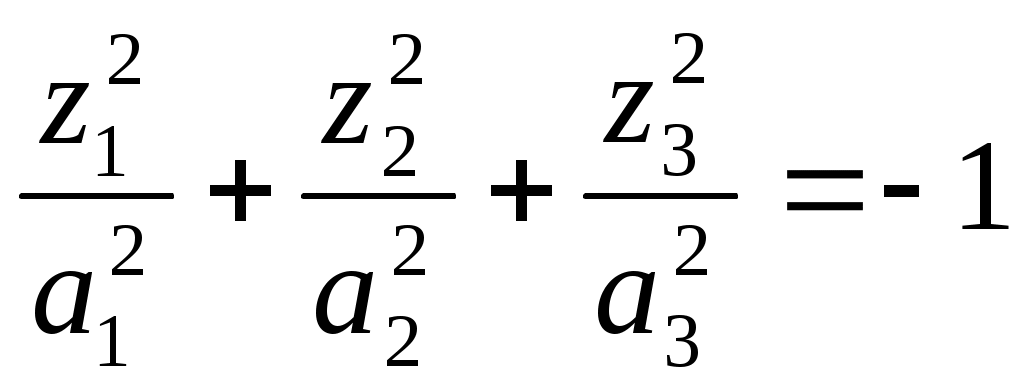 мнимый эллипсоид; мнимый эллипсоид;3) 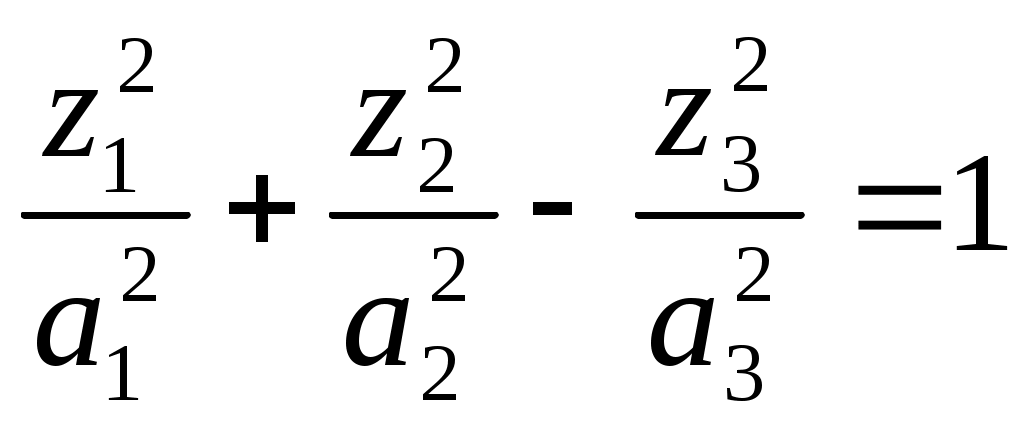 однополостный гиперболоид; однополостный гиперболоид;4) 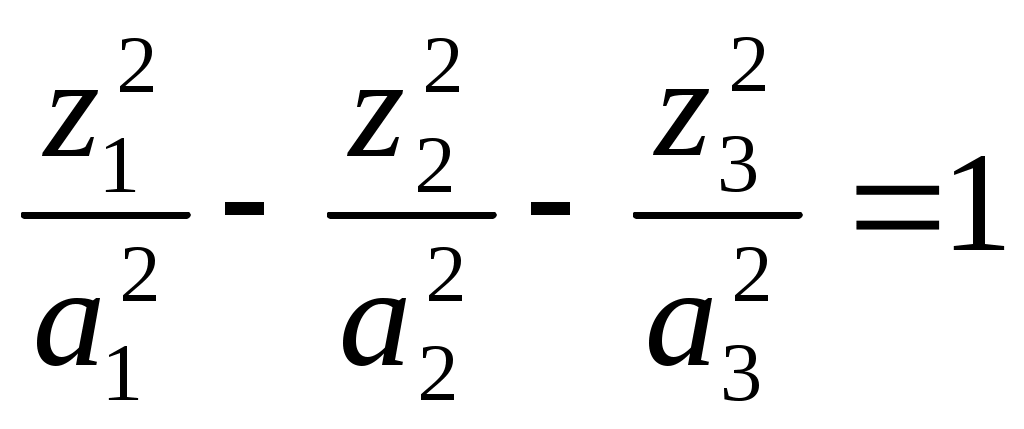 двуполостный гиперболоид. двуполостный гиперболоид.Все эллипсоиды аффинно эквивалентны и, следовательно, с точки зрения аффинной геометрии не отличаются друг от друга по своим свойствам. Однако не всякие два эллипсоида конгруэнтны и даже подобны; в связи с этим в евклидовой геометрии появляется возможность классификации эллипсоидов. Если а1, а2, а3 различны, то эллипсоид называется трехосным. Если равны какие-нибудь два из чисел а1, а2, а3, то эллипсоид называется эллипсоидом вращения. Если а1 = а2 = а3, то эллипсоид является сферой. Эта классификация инвариантна относительно движений; например, любое движение может отобразить сферу также только на сферу. Поэтому указанные виды эллипсоидов являются объектами, изучаемыми в евклидовой геометрии. Аналогичные замечания можно сделать и относительно других видов квадрик(например, можно выделить гиперболоиды вращения, конус вращения и т. п.). Случай 2. 5) 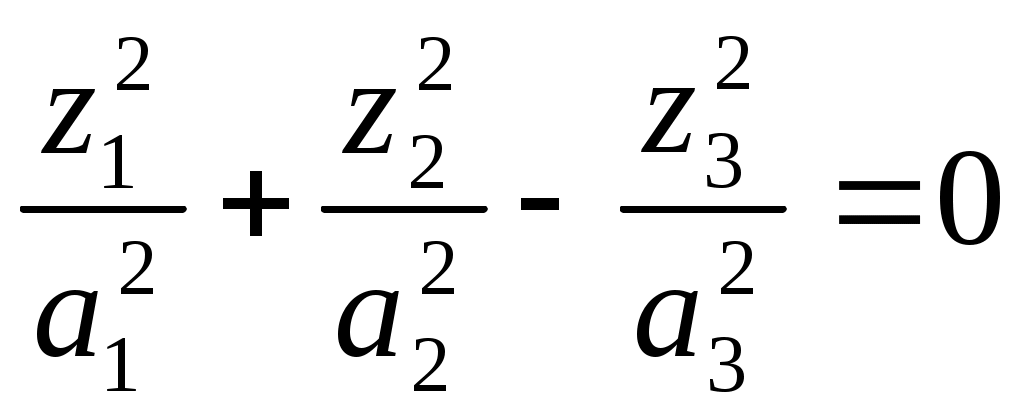 конус (при конус (при 6) 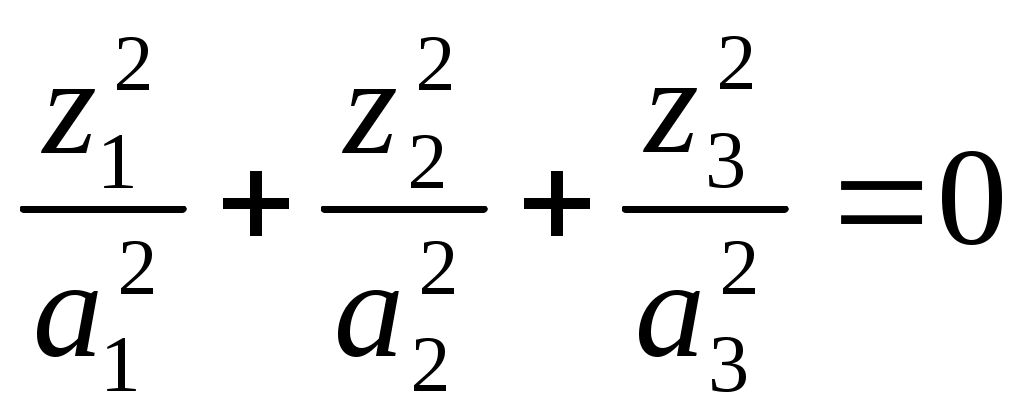 мнимый конус с вершиной в действительной точке; мнимый конус с вершиной в действительной точке;Случай 3. С помощью параллельного переноса координат по формулам 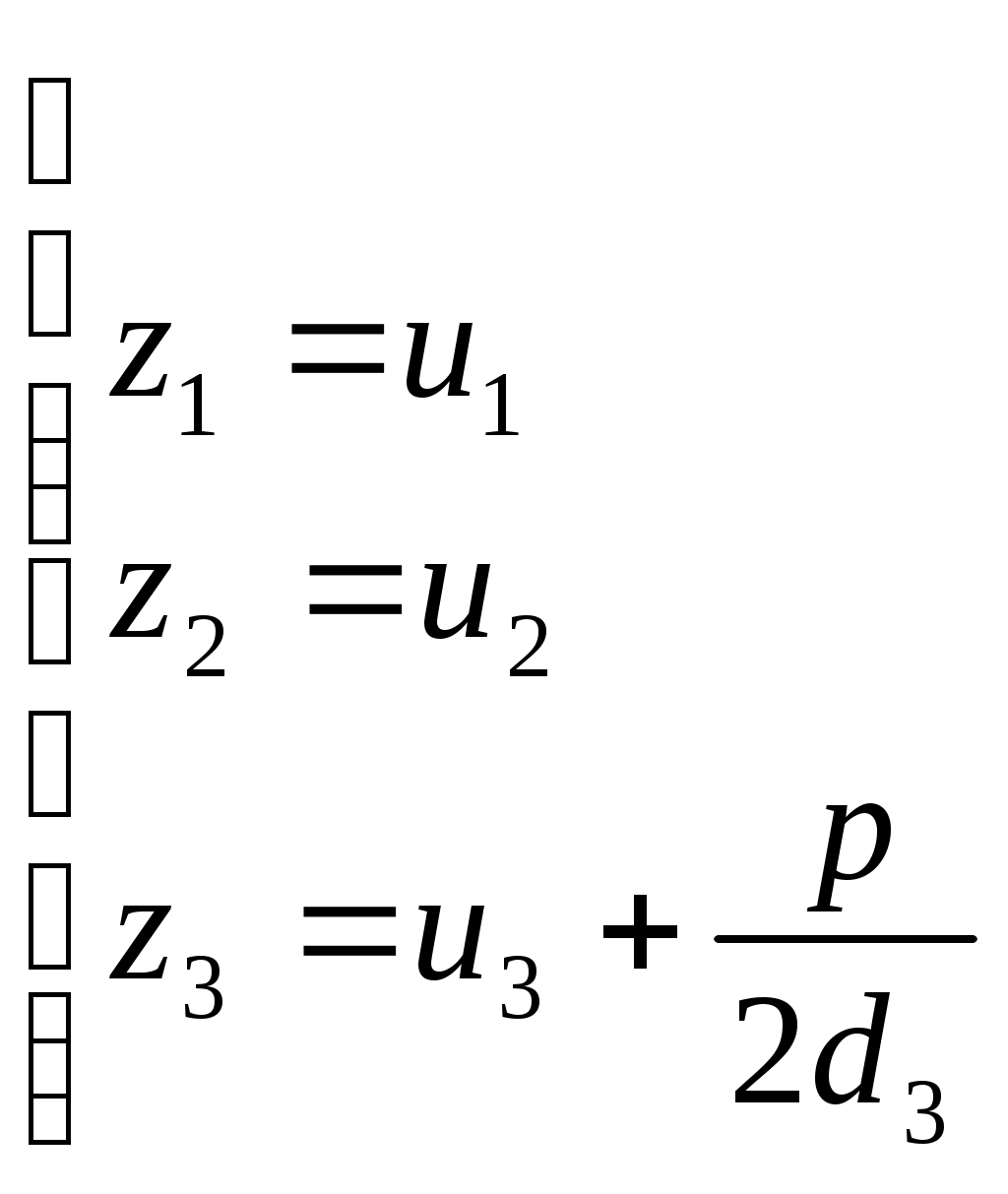 можно освободиться от свободного члена. Получим частные случаи: 7) 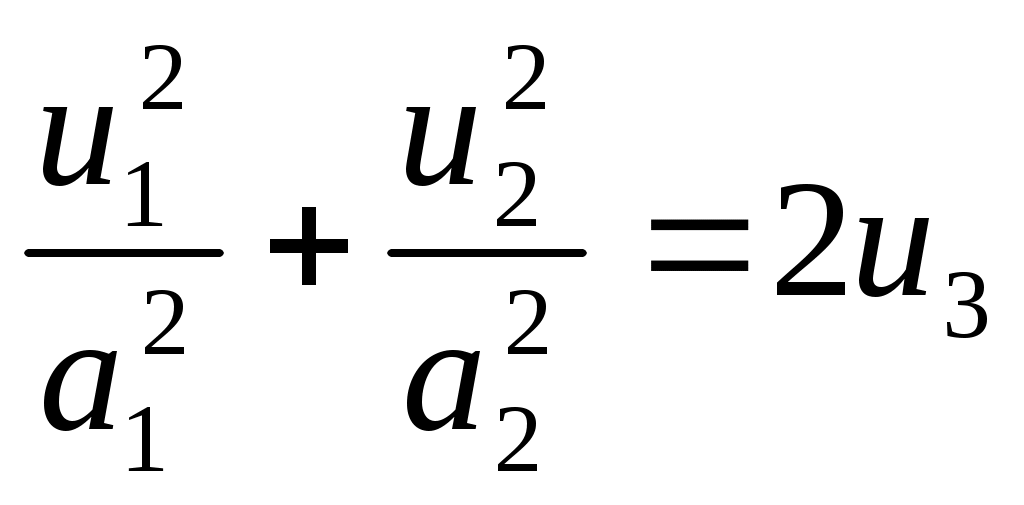 эллиптический параболоид (при эллиптический параболоид (при 8) 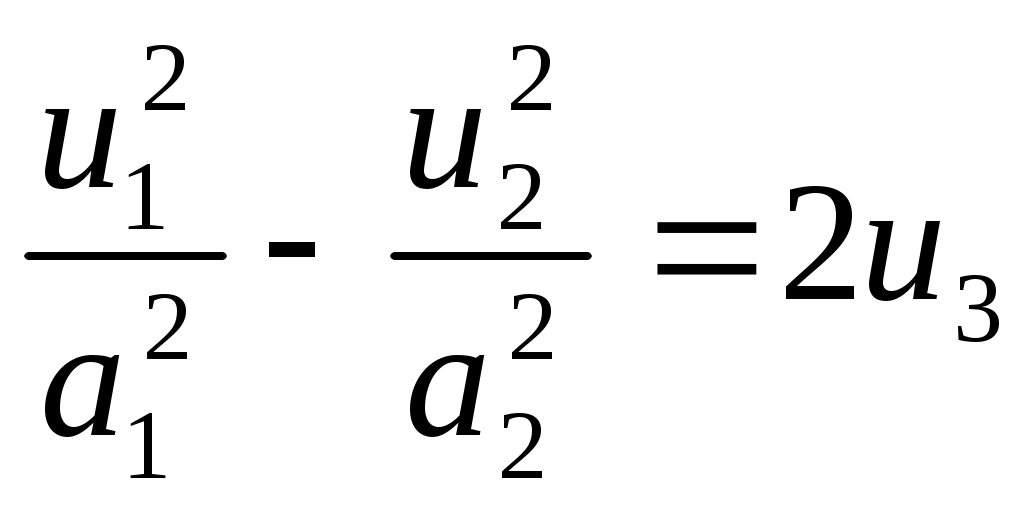 гиперболический параболоид. гиперболический параболоид.Случай 4. Цилиндрические квадрики. 1. 9) 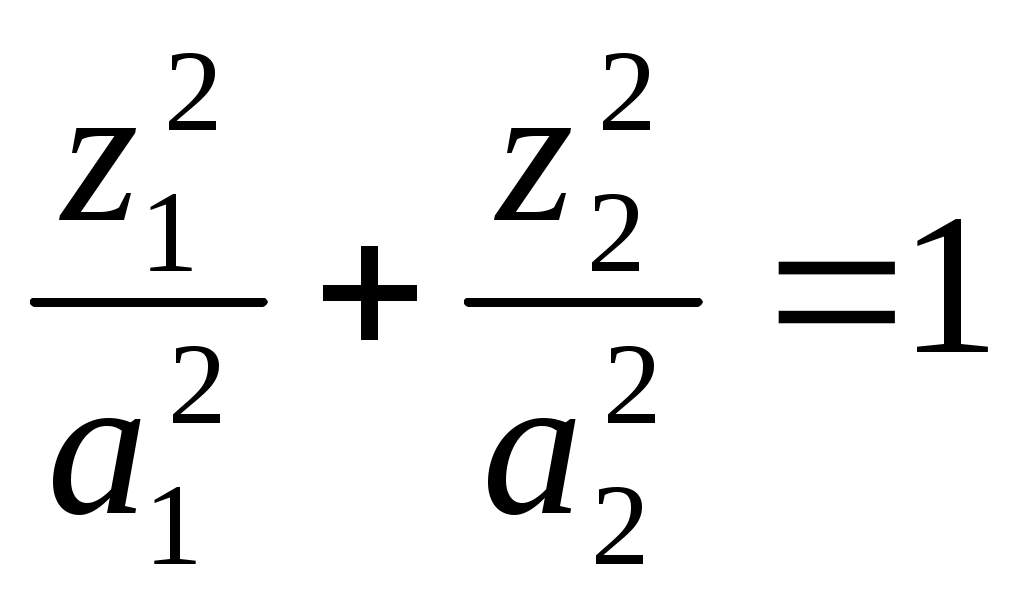 эллиптический цилиндр (при эллиптический цилиндр (при 10) 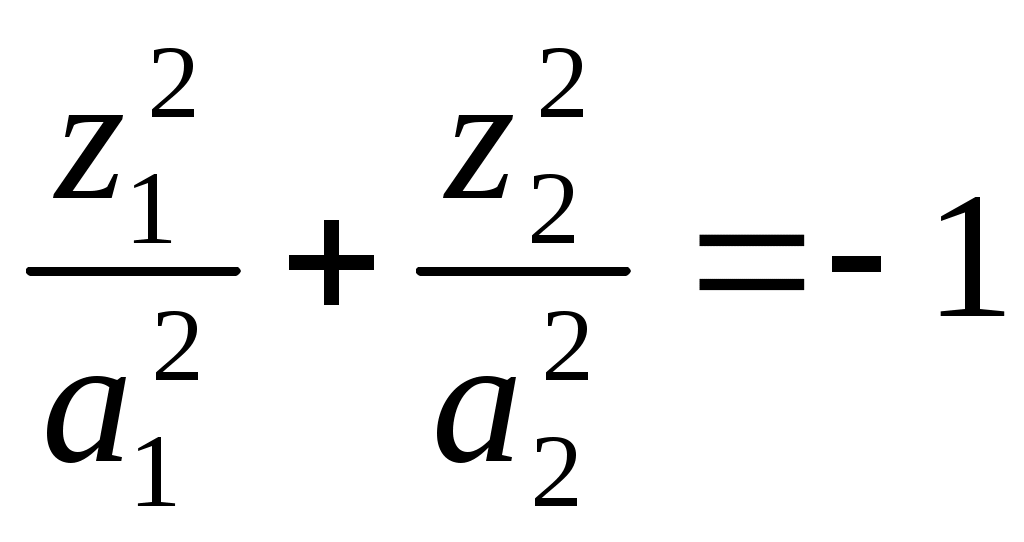 мнимый эллиптический цилиндр; мнимый эллиптический цилиндр;11) 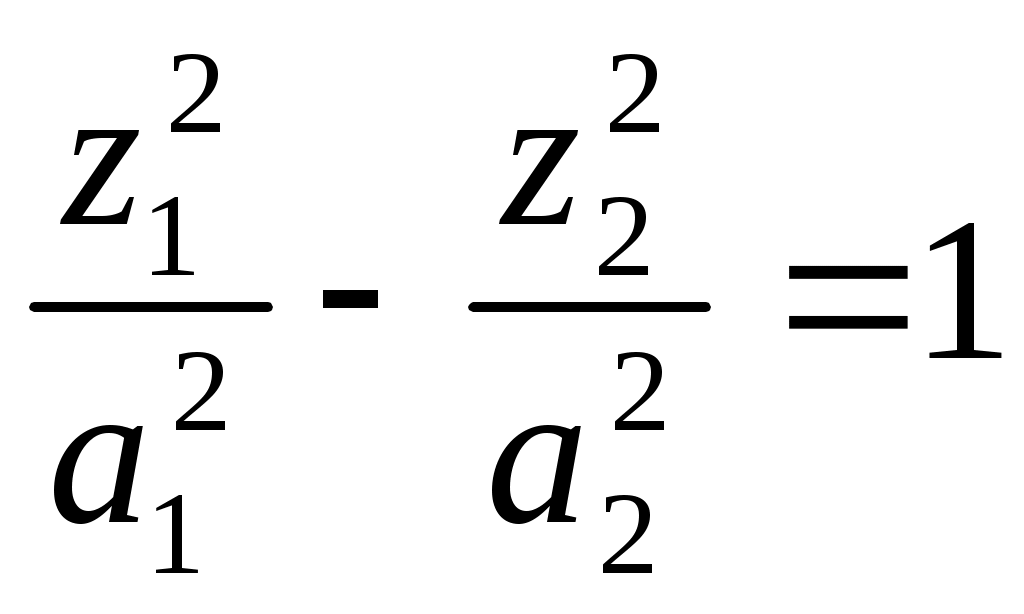 гиперболический цилиндр. гиперболический цилиндр.2. 12) 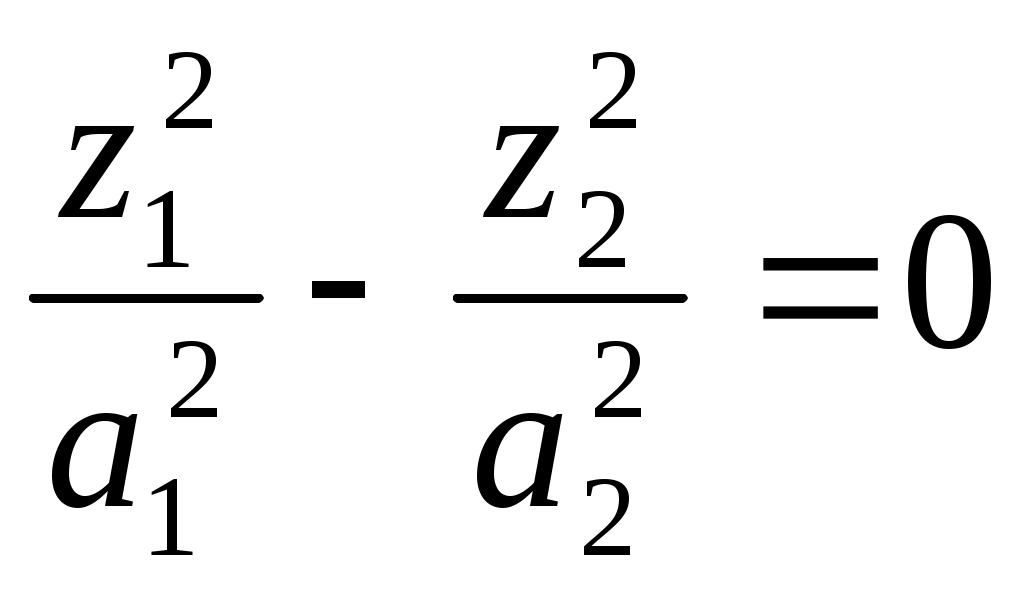 пара пересекающихся плоскостей; пара пересекающихся плоскостей;13) 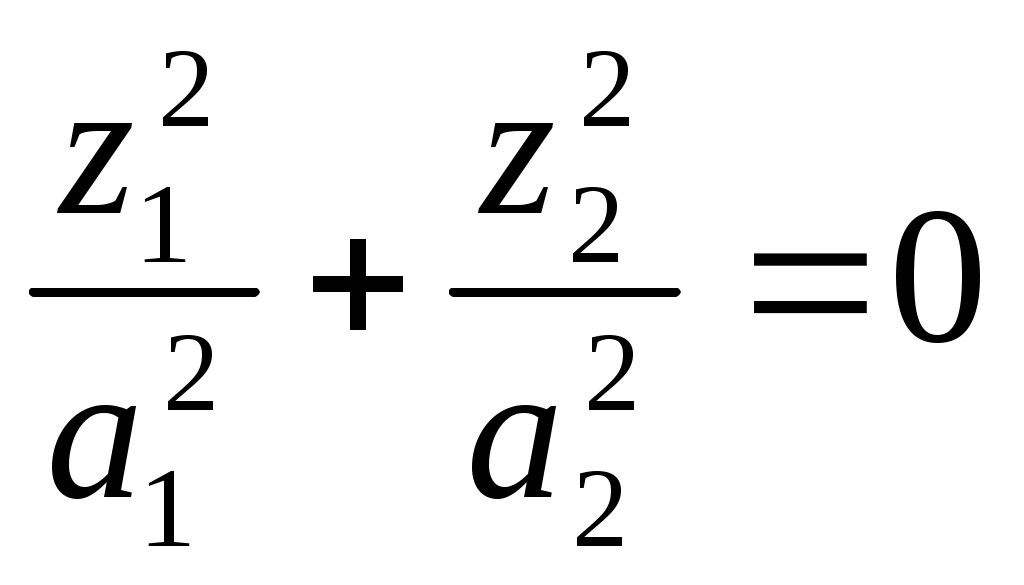 пара мнимых плоскостей, пересекающихся по действительной прямой пара мнимых плоскостей, пересекающихся по действительной прямой 3. 14) 15) 16) 4. Разделив обе части этого уравнения на С помощью ортогонального преобразования 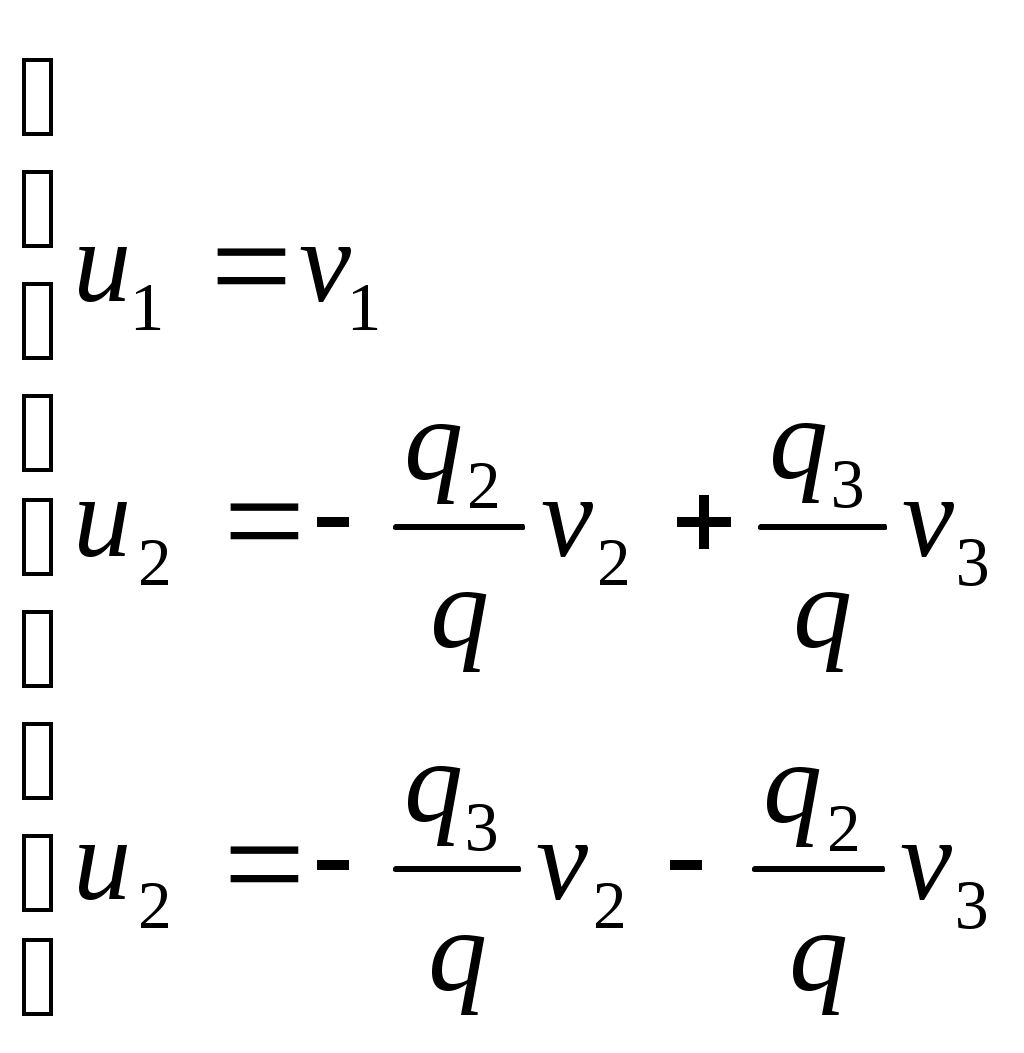 где 17) Те виды, к которым было приведено уравнение квадрики во всех рассмотренных выше случаях, называютсяканоническимивидами уравнения квадрики. Имеет место теорема о классификации квадрик в Е3: Существует семнадцать и только семнадцать поверхностей второго порядка (рассмотренных выше). ЗАКЛЮЧЕНИЕ.Теории симметричных и квадратичных форм векторных пространств и квадрик (или геометрических образов второго порядка) проективных пространств над полем развивались взаимосвязано и достаточно хорошо разработаны. Изучение произвольных рефлексивных форм над полем сведено к изучению невырожденных рефлексивных форм, а последние классифицированы вместе с симметричными и кососимметричными формами. Наряду с развитием этой теории, в исследованиях проективных пространств возрастал интерес к переходу от полей к более общим кольцам коэффициентов. Естественно, что квадрики исследуются взаимосвязано с квадратичными формами и их матрицами. В данной работе были рассмотрены квадратичные формы, их основные представления – нормальный и канонический вид. Доказана возможность приведения квадратичной формы к основным видам и указаны способы преобразования квадратичных форм. Также рассмотрено понятие квадрики, центра квадрики и приведение уравнения квадрики к нормальному виду. В работу приведена классификация квадрики, в частности классификация в двумерном аффинном и трёхмерном евклидовом пространствах. Объекты, которые мы рассмотрели, в частности аффинные квадрики, очень важны с практической точки зрения, ибо это самые простые, после прямых и плоскостей, поверхности и кривые в трёхмерном пространстве и на плоскости, которые встречаются всюду – в математике и механике, физике и астрономии. Верхушка Эйфелевой башни и верхние этажи Монпарнасской башни в ветреную погоду описывают эллипсы, у которых максимальная ось должна быть разумной величины, чтобы это не казалось опасным. А при помощи парабол проще всего выполнить сопряжение двух прямых. Поэтому теория квадратичных форм и квадрик всегда будет актуальна. ЛИТЕРАТУРА.1. Атанасян Л.С., «Геометрия», часть 1. М.:»ПРОСВЕЩЕНИЕ», 1973 г.; 2. М.Берже, «Геометрия», том 2. М.: «Мир», 1984; 3. Ефимов Н.В., Розендорн Э.Р., «Линейная алгебра и многомерная геометрия». – М. 1970 г.; 4. Парнасский И.В., Парнасская О.Е., «Многомерные пространства. Квадратичные формы и квадрики». – М.: «ПРОСВЕЩЕНИЕ», 1978 г.. 1 2 |
