Основная образовательная программа cb. 5005. 2016 Прикладная математика, фундаментальная информатика и программирование
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
Определение 1.5.Простой цикл графа  не содержащий хорд называется порожденным циклом. не содержащий хорд называется порожденным циклом.На рисунке 1.6 изображен пример порожденного цикла в графе. 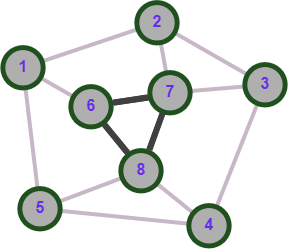 Рисунок 1.6 - Граф, черным выделен один из содержащихся в нем порожденных циклов 6-7-8-6 Определение 1.6.Простой путь, проходящий по всем узлам графа  — это гамильтонов путь. — это гамильтонов путь.На рисунке 1.7 изображен пример гамильтонова пути.  Рисунок 1.7 - Граф, черным выделен гамильтонов путь 2-7-3-4-8-6-1-5 Определение 1.7.Простой цикл, проходящий по всем узлам графа  —это гамильтонов цикл. Граф —это гамильтонов цикл. Граф  — гамильтонов, когда в нем присутствует гамильтонов цикл. — гамильтонов, когда в нем присутствует гамильтонов цикл.На рисунке 1.8 изображен пример гамильтонова пути. 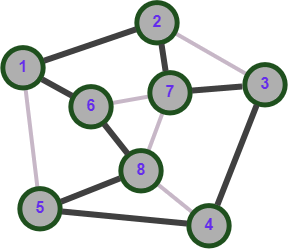 Рисунок 1.8 - Граф, черным выделен гамильтонов цикл 2-1-6-8-5-4-3-7-2 1.2. Циклическое пространство графа Нам понадобится знание о том, что такое линейное пространство. Мы будем использовать линейные пространства над полем  . Для возможности в дальнейшем обобщить теорию на ориентированные графы вместо операции сложения по модулю используем операцию симметрической разности, поскольку они эквивалентны для поля . Для возможности в дальнейшем обобщить теорию на ориентированные графы вместо операции сложения по модулю используем операцию симметрической разности, поскольку они эквивалентны для поля  . .Определение 1.8.Реберным пространством графа  называется линейное пространство над полем называется линейное пространство над полем  , и обозначается , и обозначается 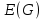 . . 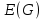 состоит из подмножеств множества состоит из подмножеств множества 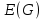 . Сумма элементов . Сумма элементов 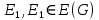 определяется как их симметрическая разность определяется как их симметрическая разность 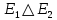 . .На рисунке 1.9 изображен пример суммы элементов.  Рисунок 1.9 - Пример суммы элементов  есть линейное пространство над есть линейное пространство над 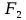 с базисом с базисом 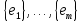 . Следовательно, . Следовательно,  . .Определение 1.9.Скалярное произведение 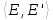 , где , где  , определяется как остаток от деления , определяется как остаток от деления 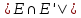 на на  . .Ортогональное дополнение подпространства 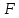 реберного пространства реберного пространства 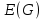 задается следующим образом: задается следующим образом: Замечание 1.1.Кроме того, элемент 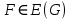 записывается в виде записывается в виде 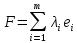 , где множитель , где множитель 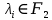 и равен единице, когда и равен единице, когда  . .При этом если 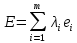 и и 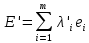 , то из скалярное произведение можно представить в виде , то из скалярное произведение можно представить в виде 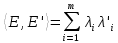 , что соответствует скалярному произведению в более общепринятом смысле. , что соответствует скалярному произведению в более общепринятом смысле. Для четного же количества ребер  истинно равенство истинно равенство  . Из-за чего нельзя прибегать к свойствам скалярного произведения над вещественным полем, так как для их доказательства необходима невырожденность. Вместе с тем, становятся невыполнимы стандартные свойства подпространства . Из-за чего нельзя прибегать к свойствам скалярного произведения над вещественным полем, так как для их доказательства необходима невырожденность. Вместе с тем, становятся невыполнимы стандартные свойства подпространства 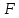 реберного пространства реберного пространства 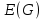 такие как такие как 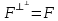 и и 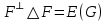 . . |
