Основная образовательная программа cb. 5005. 2016 Прикладная математика, фундаментальная информатика и программирование
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
Определение 1.10.Циклическим пространством 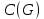 графа графа  называется подпространство называется подпространство 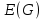 , сформированное из реберных множеств простых циклов. , сформированное из реберных множеств простых циклов.В циклическом же пространстве содержится полезная для данного исследования информация о графе  . .Лемма 1.1.В графе  реберные множества порожденных циклов формируют циклическое пространство реберные множества порожденных циклов формируют циклическое пространство 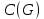 . . Доказательство.Пространство 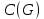 сформировано множествами ребер простых циклов, поэтому если показать, что для простого цикла сформировано множествами ребер простых циклов, поэтому если показать, что для простого цикла  его реберное множество сформировано множествами ребер порожденных циклов, то мы получим требуемое. Воспользуемся индукцией по количеству ребер. Пусть его реберное множество сформировано множествами ребер порожденных циклов, то мы получим требуемое. Воспользуемся индукцией по количеству ребер. Пусть  — не порожденный цикл. Тогда простой цикл — не порожденный цикл. Тогда простой цикл  имеет хорду имеет хорду 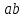 , которая разделяет его на два подцикла , которая разделяет его на два подцикла 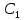 и и 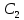 . Из чего следует, что . Из чего следует, что 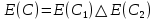 , а для , а для 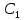 и и 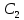 утверждение доказано. ∎ утверждение доказано. ∎1.3. Пространство разрезов Определение 1.11.Разрезом называется множество ребер производящие произвольное разбиение множества узлов 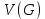 на два непересекающихся множества на два непересекающихся множества 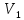 и и 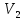 , обозначается как , обозначается как 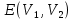 . . Пространство разрезов 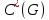 — это подпространство — это подпространство 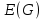 , сформированное всем множеством разрезов. , сформированное всем множеством разрезов. Для узлов 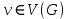 разрез из всех смежных узлу разрез из всех смежных узлу 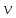 ребер будет определяться как ребер будет определяться как 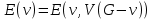 . .Замечание 1.2.Разрез состоит только из ребер графа, разделяющих любые две части множества его узлов. Лемма 1.2.1. Если 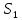 и и 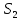 — два разреза, то и — два разреза, то и 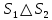 — разрез. — разрез. 2. Множество 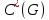 порождено всеми разрезами графа порождено всеми разрезами графа  и пустым множеством и пустым множеством 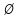 . . 3. Разрезы 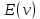 формируют формируют 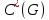 . .Доказательство.1. Пусть разрезы 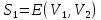 и и 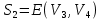 . Тогда . Тогда 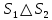 — множество, состоящее из тех ребер, что пересекают только одну из пары разрезов, то есть концы ребер располагаются в смежных частях одного из двух разбиений — множество, состоящее из тех ребер, что пересекают только одну из пары разрезов, то есть концы ребер располагаются в смежных частях одного из двух разбиений 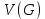 . Поэтому и . Поэтому и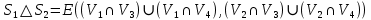 — разрез. 2. Следовательно, все множество разрезов замкнуто относительно операции симметрической разности. 3. Пусть 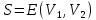 — любой из разрезов. Тогда сумма всех разрезов вида — любой из разрезов. Тогда сумма всех разрезов вида 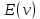 , где , где 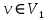 есть есть 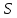 , так как сумма — это операция симметрической разности, из чего следует, что при сложении разрезов все ребра между узлами , так как сумма — это операция симметрической разности, из чего следует, что при сложении разрезов все ребра между узлами 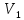 сократятся и останутся лишь ребра разреза сократятся и останутся лишь ребра разреза 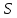 . ∎ . ∎ |
